Odds ratio vs. relative risk

On this page
📊 The Statistical Precision Matrix: Decoding Clinical Evidence
You'll master the critical distinction between odds ratios and relative risk-two measures that quantify association but diverge in meaning, calculation, and appropriate use across study designs. Understanding when each metric applies, how to interpret their magnitudes, and why confusing them leads to clinical misinterpretation will sharpen your ability to critically appraise literature and translate statistical findings into patient care decisions. We'll build from foundational calculations through study design selection, advanced diagnostic statistics, and real-world evidence synthesis so you can confidently navigate any research paper or clinical guideline.
📌 Remember: CORE - Case-control uses Odds Ratio, Cohort uses Relative Risk, Experimental studies prefer RR for direct risk interpretation
The Mathematical Foundation
Both measures quantify associations between exposures and outcomes, but through different mathematical lenses:
-
Odds Ratio: Compares odds of disease in exposed vs. unexposed groups
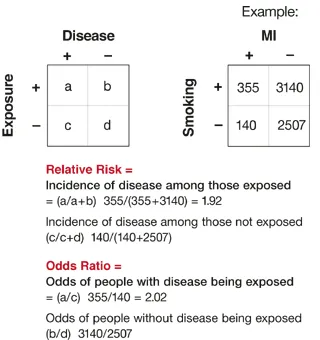
- Formula: OR = (a×d)/(b×c) from 2×2 table
- Range: 0 to infinity (1 = no association)
- Interpretation: Odds of disease X times higher in exposed group
-
Relative Risk: Compares probability of disease in exposed vs. unexposed
- Formula: RR = [a/(a+b)] / [c/(c+d)]
- Range: 0 to infinity (1 = no association)
- Interpretation: Risk of disease X times higher in exposed group
⭐ Clinical Pearl: When disease prevalence exceeds 10%, OR systematically overestimates the true relative risk, sometimes by 200-300% in high-prevalence conditions
| Measure | Study Design | Calculation | Interpretation | Prevalence Sensitivity |
|---|---|---|---|---|
| Odds Ratio | Case-control, Cross-sectional | (a×d)/(b×c) | Odds comparison | High bias when >10% |
| Relative Risk | Cohort, RCT | Risk₁/Risk₂ | Direct risk ratio | Accurate at all levels |
| Risk Difference | Cohort, RCT | Risk₁ - Risk₂ | Absolute impact | Clinical significance |
| Number Needed to Treat | Intervention studies | 1/Risk Difference | Treatment efficiency | Cost-effectiveness |
| Attributable Risk | Population studies | (RR-1)/RR × 100% | Population burden | Public health planning |
The clinical significance emerges when interpreting treatment effects: an OR of 2.5 might represent an actual RR of 1.8 in moderate-prevalence conditions, dramatically altering treatment recommendations and patient counseling approaches.
📊 The Statistical Precision Matrix: Decoding Clinical Evidence
⚖️ The Epidemiological Compass: Study Design Navigation
📌 Remember: DISCO - Disease status known first = case-control = OR; Incidence Studied Chronologically = Observational cohort = RR
Study Design Architecture
The methodological framework determines statistical approach through temporal relationships:
-
Case-Control Studies
- Start with disease status (cases vs. controls)
- Look backward to exposure history
- Cannot calculate true incidence rates
- OR only valid measure for association strength
- Efficient for rare diseases (<5% prevalence)
-
Cohort Studies
- Start with exposure status (exposed vs. unexposed)
- Follow forward to disease development
- Calculate true incidence rates in both groups
- RR provides direct risk interpretation
- Required for common diseases (>10% prevalence)
-
Cross-Sectional Studies
- Simultaneous assessment of exposure and disease
- Prevalence ratios approximate RR
- OR available but may overestimate associations
- Limited temporal relationship establishment
⭐ Clinical Pearl: Randomized controlled trials always report RR or risk difference because randomization ensures balanced baseline characteristics, making direct risk comparison valid and clinically interpretable
| Study Type | Temporal Direction | Primary Measure | Validity Conditions | Clinical Application |
|---|---|---|---|---|
| Case-Control | Retrospective | Odds Ratio | Rare disease (<5%) | Hypothesis generation |
| Cohort | Prospective | Relative Risk | Any prevalence | Causation assessment |
| Cross-Sectional | Point-in-time | Prevalence Ratio | Stable conditions | Screening programs |
| RCT | Prospective | Relative Risk | Intervention effects | Treatment decisions |
| Meta-Analysis | Combined | Both OR/RR | Homogeneous studies | Evidence synthesis |
Understanding design-measure relationships prevents statistical misinterpretation: a case-control study reporting RR commits a fundamental methodological error, while a cohort study can legitimately report both OR and RR, though RR provides superior clinical interpretation.
⚖️ The Epidemiological Compass: Study Design Navigation
🔢 The Calculation Engine: Mathematical Precision Mastery
📌 Remember: ABCD - Affected exposed, Benign exposed, Cases unexposed, Disease-free unexposed (standard 2×2 table layout for consistent calculations)
The Mathematical Framework
Standard 2×2 table configuration enables systematic calculation:
Standard 2×2 Table Layout:
| Disease + | Disease - | Total | |
|---|---|---|---|
| Exposed + | a | b | a+b |
| Exposed - | c | d | c+d |
| Total | a+c | b+d | N |
- OR = (a×d)/(b×c)
- Odds in exposed = a/b
- Odds in unexposed = c/d
- OR = (a/b)/(c/d) = (a×d)/(b×c)
Relative Risk Calculation:
- RR = [a/(a+b)] / [c/(c+d)]
- Risk in exposed = a/(a+b)
- Risk in unexposed = c/(c+d)
- RR = Risk₁/Risk₂
⭐ Clinical Pearl: When calculating by hand, always verify your 2×2 table orientation - 90% of calculation errors stem from incorrect cell placement, particularly confusing exposure status with outcome status
Worked Clinical Example
Smoking and Lung Cancer Study (Cohort Design):
- Smokers with lung cancer: 84 patients
- Smokers without lung cancer: 2,916 patients
- Non-smokers with lung cancer: 12 patients
- Non-smokers without lung cancer: 3,988 patients
| Lung Cancer + | Lung Cancer - | Total | |
|---|---|---|---|
| Smokers | 84 | 2,916 | 3,000 |
| Non-smokers | 12 | 3,988 | 4,000 |
| Total | 96 | 6,904 | 7,000 |
- Risk in smokers = 84/3,000 = 0.028 (2.8%)
- Risk in non-smokers = 12/4,000 = 0.003 (0.3%)
- RR = 0.028/0.003 = 9.33
Odds Ratio Calculation:
- OR = (84×3,988)/(2,916×12) = 9.57
💡 Master This: In this example, OR (9.57) slightly overestimates RR (9.33) despite low disease prevalence (1.4%) because the exposure (smoking) is common (43% of population) - high exposure prevalence also affects OR-RR relationships
The minimal difference between OR and RR here (2.6% overestimation) confirms the rare disease assumption validity, but demonstrates that exposure prevalence also influences the relationship between these measures.
🔢 The Calculation Engine: Mathematical Precision Mastery
🎯 The Clinical Translation Matrix: From Numbers to Decisions
📌 Remember: MAGIC - Magnitude matters, Assess confidence intervals, Generate clinical context, Interpret baseline risk, Consider absolute differences
Interpretation Framework Hierarchy
Clinical significance emerges through systematic interpretation layers:
-
Magnitude Assessment
- OR/RR = 1.0: No association (null effect)
- OR/RR = 1.1-1.5: Weak association (10-50% increase)
- OR/RR = 1.5-3.0: Moderate association (50-200% increase)
- OR/RR = 3.0-10.0: Strong association (200-900% increase)
- OR/RR >10.0: Very strong association (>900% increase)
-
Confidence Interval Evaluation
- 95% CI includes 1.0: Not statistically significant
- 95% CI excludes 1.0: Statistically significant association
- Narrow CI: Precise estimate, large sample size
- Wide CI: Imprecise estimate, small sample or rare events
-
Clinical Context Integration
- Baseline risk assessment: High vs. low risk populations
- Absolute risk difference: Clinical impact magnitude
- Number needed to treat/harm: Practical treatment implications
- Cost-effectiveness: Resource allocation considerations
⭐ Clinical Pearl: An OR of 2.0 with 95% CI: 1.8-2.2 indicates a 100% increase in odds with high precision, but if baseline risk is 0.1%, absolute risk only increases to 0.2% - statistically significant but clinically minimal impact
| Scenario | OR Value | RR Value | Clinical Interpretation | Action Required |
|---|---|---|---|---|
| Rare Disease | 2.5 | ~2.5 | 150% odds increase | Investigate causation |
| Common Disease | 2.5 | 1.8 | 80% risk increase | Immediate intervention |
| Protective Factor | 0.4 | 0.6 | 40% risk reduction | Promote intervention |
| Null Association | 1.1 | 1.0 | No meaningful effect | Continue monitoring |
| Strong Association | 8.0 | 5.2 | 420% risk increase** | Urgent public health action |
💡 Master This: Always convert relative measures to absolute risk differences for patient counseling - telling a patient their risk "doubles" (RR=2.0) sounds alarming, but explaining an increase from 0.1% to 0.2% (absolute difference 0.1%) provides proper perspective for informed decision-making
Understanding these interpretation frameworks enables evidence-based medicine application, transforming statistical abstractions into concrete clinical recommendations that improve patient outcomes and resource utilization.
🎯 The Clinical Translation Matrix: From Numbers to Decisions
🔬 The Precision Diagnostic Engine: Advanced Statistical Discrimination
📌 Remember: RADAR - Rare disease assumption, Adjustment for confounders, Dose-response relationships, Absolute measures matter, Replication across populations
The Rare Disease Assumption Deep Dive
Mathematical relationship between OR and RR depends critically on outcome prevalence:
-
When OR ≈ RR (Rare Disease Assumption Valid)
- Disease prevalence <5%: OR within 10% of true RR
- Disease prevalence <10%: OR within 20% of true RR
- Case-control studies provide valid effect estimates
- Clinical interpretation remains accurate
-
When OR Overestimates RR (Common Disease)
- Disease prevalence >20%: OR may exceed RR by 50-100%
- Disease prevalence >50%: OR can exceed RR by 200-300%
- Case-control studies systematically bias effect estimates
- Clinical interpretation becomes misleading
Mathematical Conversion Formula: RR = OR / [(1-P₀) + (P₀ × OR)] Where P₀ = baseline risk in unexposed group
⭐ Clinical Pearl: In cardiovascular disease research (baseline risk 15-25%), an OR of 3.0 typically corresponds to an RR of 2.2-2.5 - this 20-25% overestimation significantly impacts clinical guidelines and treatment recommendations
Confounding and Adjustment Strategies
Statistical adjustment reveals true associations by controlling for confounding variables:
| Adjustment Method | Application | Interpretation | Limitations |
|---|---|---|---|
| Crude OR/RR | Unadjusted analysis | Biased estimates | Confounding present |
| Stratified Analysis | Mantel-Haenszel | Confounder-specific | Limited variables |
| Multivariable Regression | Logistic/Cox models | Multiple adjustments | Model assumptions |
| Propensity Scores | Matching/weighting | Balanced covariates | Unmeasured confounding |
| Instrumental Variables | Natural experiments | Causal inference | Strong assumptions |
Dose-Response Relationships:
- Linear trend: Each unit increase → consistent OR/RR change
- Threshold effect: No effect below critical exposure level
- Saturation effect: Diminishing returns at high exposure levels
- U-shaped curve: Protective at moderate levels, harmful at extremes
Population Attributable Risk: PAR% = (RR-1)/RR × Pe × 100% Where Pe = proportion of population exposed
💡 Master This: Adjusted OR of 1.8 (95% CI: 1.4-2.3) after controlling for age, sex, smoking, and comorbidities provides stronger causal evidence than crude OR of 2.5 (95% CI: 2.1-3.0) - adjustment magnitude and direction reveal confounding patterns and strengthen causal inference
Understanding these advanced concepts enables critical appraisal of medical literature, recognition of methodological limitations, and appropriate application of epidemiological evidence to clinical practice decisions.
🔬 The Precision Diagnostic Engine: Advanced Statistical Discrimination
🌐 The Evidence Integration Network: Meta-Analysis and Systematic Synthesis
📌 Remember: FOREST - Fixed vs random effects, Outcome measure consistency, Random effects for heterogeneity, Effect size pooling, Subgroup analysis, Test for publication bias
Meta-Analysis Methodology Framework
Evidence synthesis requires systematic approaches to combining effect estimates:
-
Study Selection Criteria
- Homogeneous populations: Similar baseline characteristics
- Consistent exposure definitions: Standardized measurement approaches
- Comparable outcomes: Uniform diagnostic criteria
- Adequate follow-up: Sufficient observation periods
- Quality assessment: Risk of bias evaluation
-
Statistical Pooling Strategies
- Fixed Effects Model: Assumes single true effect size
- Random Effects Model: Accounts for between-study variation
- Heterogeneity Assessment: I² statistic interpretation
- Sensitivity Analysis: Influence of individual studies
- Subgroup Analysis: Population-specific effects
⭐ Clinical Pearl: When combining case-control (OR) and cohort (RR) studies in meta-analysis, convert all estimates to log scale, pool using generic inverse variance, then back-transform - this approach maintains statistical validity while maximizing available evidence
Heterogeneity and Clinical Interpretation
Between-study variation affects pooled estimate validity:
| I² Statistic | Heterogeneity Level | Interpretation Strategy | Clinical Action |
|---|---|---|---|
| 0-25% | Low | Fixed effects valid | Apply pooled estimate |
| 25-50% | Moderate | Random effects preferred | Consider subgroups |
| 50-75% | Substantial | Explore sources | Population-specific estimates |
| 75-100% | Considerable | Avoid pooling | Narrative synthesis |
Systematic evaluation prevents overestimation of treatment effects:
- Funnel Plot Analysis: Visual assessment of small-study effects
- Egger's Test: Statistical test for publication bias (p<0.10 significant)
- Trim-and-Fill: Imputation of missing studies
- Fail-Safe N: Number of null studies needed to change conclusions
- Registry Search: Identification of unpublished trials
Clinical Application Framework:
Cardiovascular Prevention Meta-Analysis Example:
- 18 studies included (12 cohort, 6 case-control)
- Pooled OR: 0.72 (95% CI: 0.65-0.80)
- I² = 34%: Moderate heterogeneity
- Subgroup by study design: Cohort RR = 0.75, Case-control OR = 0.68
- Clinical interpretation: 25-32% risk reduction across populations
💡 Master This: Meta-analysis pooled OR of 0.65 (95% CI: 0.55-0.77) with I² = 15% provides Level 1 evidence for 35% risk reduction, but always examine individual study characteristics, population diversity, and outcome definitions before clinical application
Understanding meta-analysis principles enables critical evaluation of systematic reviews, appropriate application of pooled estimates, and recognition of evidence limitations that affect clinical decision-making and guideline development.
🌐 The Evidence Integration Network: Meta-Analysis and Systematic Synthesis
🎯 The Clinical Mastery Arsenal: Rapid-Fire Evidence Application
📌 Remember: RAPID - Recognize study design, Assess baseline risk, Pool absolute differences, Interpret confidence intervals, Determine clinical significance
Essential Clinical Arsenal
Quick Recognition Patterns:
- Case-control study → OR only → Check rare disease assumption
- Cohort/RCT study → RR preferred → Direct risk interpretation
- OR >2.0 with common disease → Likely overestimate → Calculate true RR
- Wide confidence intervals → Imprecise estimate → Larger studies needed
- Statistical significance ≠ Clinical significance → Check absolute differences
Rapid Calculation Tools:
| Clinical Scenario | Quick Formula | Interpretation Threshold |
|---|---|---|
| OR to RR Conversion | RR ≈ OR/(1-P₀+P₀×OR) | Use when P₀ >10% |
| Absolute Risk Difference | ARD = Risk₁ - Risk₂ | Clinically significant >1% |
| Number Needed to Treat | NNT = 1/ARD | Cost-effective <100 |
| Population Impact | PAR% = (RR-1)/RR × Pe | Public health priority >10% |
| Clinical Significance | Cohen's h effect size | Large effect >0.8 |
- ✅ Study design appropriate for research question
- ✅ Sample size adequate for statistical power
- ✅ Confidence intervals exclude null value
- ✅ Baseline characteristics balanced between groups
- ✅ Follow-up duration sufficient for outcome development
- ✅ Confounding variables adequately controlled
- ✅ Clinical significance matches statistical significance
⭐ Clinical Pearl: For patient counseling, always present both relative and absolute risk: "This treatment reduces your risk by 50% (relative) - from 4 in 100 to 2 in 100 patients (absolute)" - this dual presentation enables truly informed consent
💡 Master This: Develop pattern recognition for common OR/RR values: 1.5 = modest effect, 2.0 = moderate effect, 3.0 = strong effect, 5.0 = very strong effect - but always contextualize with baseline risk, confidence intervals, and absolute differences for complete clinical assessment
This clinical mastery framework enables rapid evidence evaluation, appropriate statistical interpretation, and effective translation of research findings into evidence-based patient care decisions that optimize clinical outcomes and healthcare resource utilization.
🎯 The Clinical Mastery Arsenal: Rapid-Fire Evidence Application
Practice Questions: Odds ratio vs. relative risk
Test your understanding with these related questions
A research team develops a new monoclonal antibody checkpoint inhibitor for advanced melanoma that has shown promise in animal studies as well as high efficacy and low toxicity in early phase human clinical trials. The research team would now like to compare this drug to existing standard of care immunotherapy for advanced melanoma. The research team decides to conduct a non-randomized study where the novel drug will be offered to patients who are deemed to be at risk for toxicity with the current standard of care immunotherapy, while patients without such risk factors will receive the standard treatment. Which of the following best describes the level of evidence that this study can offer?












