Area under the curve calculations US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Area under the curve calculations. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Area under the curve calculations US Medical PG Question 1: A 35-year-old woman is started on a new experimental intravenous drug X. In order to make sure that she is able to take this drug safely, the physician in charge of her care calculates the appropriate doses to give to this patient. Data on the properties of drug X from a subject with a similar body composition to the patient is provided below:
Weight: 100 kg
Dose provided: 1500 mg
Serum concentration 15 mg/dL
Bioavailability: 1
If the patient has a weight of 60 kg and the target serum concentration is 10 mg/dL, which of the following best represents the loading dose of drug X that should be given to this patient?
- A. 300 mg
- B. 450 mg
- C. 150 mg
- D. 1000 mg
- E. 600 mg (Correct Answer)
Area under the curve calculations Explanation: ***600 mg***
- First, calculate the **volume of distribution (Vd)** using the provided data: **Vd = Total Dose / Serum Concentration**. Converting units: 15 mg/dL = 150 mg/L. Therefore, Vd = 1500 mg / 150 mg/L = **10 L** (for the 100 kg subject).
- Since the Vd value is for a 100 kg person, Vd per kg = 10 L / 100 kg = **0.1 L/kg**. For the 60 kg patient, the Vd = 0.1 L/kg × 60 kg = **6 L**.
- The **loading dose = Target Serum Concentration × Vd / Bioavailability**. Converting target concentration: 10 mg/dL = 100 mg/L. Therefore: (100 mg/L × 6 L) / 1 = **600 mg**.
*300 mg*
- This value is obtained if an incorrect **Vd** or target concentration was used, potentially through miscalculation or incorrect unit conversion.
- For instance, if the **Vd** was inaccurately calculated at 3 L (instead of 6 L), this could lead to the incorrect answer.
*450 mg*
- This result might occur if the **Vd calculation** was flawed or if the target concentration was incorrectly interpreted.
- A potential error could involve using a Vd of 4.5 L which would result in 450 mg, or if the drug amount was simply prorated by weight without properly considering the Vd per kg.
*150 mg*
- This value suggests a significant error in the calculation of the **volume of distribution** or the target concentration.
- It might be obtained if the **Vd** was mistakenly taken as 1.5 L or if the dose was divided by the original serum concentration without accounting for the new patient's weight and desired concentration.
*1000 mg*
- This value is significantly higher than the correct answer, indicating an overestimation of the **Vd** or target concentration.
- It could result from using the original dose (1500 mg) and attempting to scale it incorrectly by weight alone (1500 mg × 60/100 = 900 mg, close to 1000), or if unit conversions were mishandled during the Vd determination.
Area under the curve calculations US Medical PG Question 2: A 68-year-old man undergoes successful mechanical prosthetic aortic valve replacement for severe aortic valve stenosis. After the procedure, he is started on an oral medication and instructed that he should take for the rest of his life and that he should avoid consuming large amounts of dark-green, leafy vegetables. Which of the following laboratory parameters should be regularly monitored to guide dosing of this drug?
- A. D-dimer
- B. Anti-factor Xa activity
- C. Activated partial thromboplastin time
- D. Prothrombin time (Correct Answer)
- E. Thrombin time
Area under the curve calculations Explanation: ***Prothrombin time***
- **Warfarin** is the standard chronic anticoagulant post-mechanical valve replacement, and its dosing is monitored using the **prothrombin time (PT)**, reported as the **International Normalized Ratio (INR)**.
- The avoidance of dark-green, leafy vegetables indicates a **Vitamin K antagonist**, which is warfarin.
*D-dimer*
- **D-dimer** levels are primarily used to rule out **venous thromboembolism (VTE)** and are not used for routine monitoring of chronic anticoagulation.
- Elevated D-dimer indicates recent or ongoing **fibrinolysis**, which is not directly targeted by warfarin therapy.
*Anti-factor Xa activity*
- **Anti-factor Xa activity** is used to monitor the anticoagulant effect of **low molecular weight heparins (LMWH)** or **direct oral anticoagulants (DOACs)** like rivaroxaban or apixaban.
- This patient is on a vitamin K antagonist, not an anti-Xa inhibitor.
*Activated partial thromboplastin time*
- The **activated partial thromboplastin time (aPTT)** is used to monitor patients receiving **unfractionated heparin**, not warfarin.
- While both heparin and warfarin are anticoagulants, they act on different parts of the coagulation cascade and are monitored differently.
*Thrombin time*
- **Thrombin time (TT)** measures the time it takes for plasma to clot after adding thrombin, and it is primarily used to detect inherited or acquired **fibrinogen disorders** or to monitor **direct thrombin inhibitors**.
- It is not routinely used for monitoring warfarin therapy.
Area under the curve calculations US Medical PG Question 3: A scientist is studying the excretion of a novel toxin X by the kidney in order to understand the dynamics of this new substance. He discovers that this new toxin X has a clearance that is half that of inulin in a particular patient. This patient's filtration fraction is 20% and his para-aminohippuric acid (PAH) dynamics are as follows:
Urine volume: 100 mL/min
Urine PAH concentration: 30 mg/mL
Plasma PAH concentration: 5 mg/mL
Given these findings, what is the clearance of the novel toxin X?
- A. 1,500 mL/min
- B. 600 mL/min
- C. 300 mL/min
- D. 60 mL/min (Correct Answer)
- E. 120 mL/min
Area under the curve calculations Explanation: ***60 ml/min***
- First, calculate the **renal plasma flow (RPF)** using PAH clearance: RPF = (Urine PAH conc. × Urine vol.) / Plasma PAH conc. = (30 mg/mL × 100 mL/min) / 5 mg/mL = 600 mL/min.
- Next, calculate the **glomerular filtration rate (GFR)**, which is the clearance of inulin. GFR = RPF × Filtration Fraction = 600 mL/min × 0.20 = 120 mL/min. Toxin X clearance is half of inulin clearance, so 120 mL/min / 2 = **60 mL/min**.
*1,500 ml/min*
- This value is likely obtained if an incorrect formula or conversion was made, possibly by misinterpreting the units or the relationship between GFR, RPF, and filtration fraction.
- It significantly overestimates the clearance for a substance that is cleared at half the rate of inulin.
*600 ml/min*
- This value represents the **renal plasma flow (RPF)**, calculated using the PAH clearance data.
- It does not account for the filtration fraction or the fact that toxin X clearance is half of inulin clearance (GFR).
*300 ml/min*
- This value would be obtained if the renal plasma flow (RPF) was incorrectly halved, or if an intermediate calculation was misinterpreted as the final answer.
- It does not align with the given filtration fraction and the relationship between toxin X and inulin clearance.
*120 ml/min*
- This value represents the **glomerular filtration rate (GFR)**, which is equal to the clearance of inulin (RPF × Filtration Fraction = 600 mL/min × 0.20 = 120 mL/min).
- The question states that the clearance of toxin X is **half** that of inulin, so this is an intermediate step, not the final answer.
Area under the curve calculations US Medical PG Question 4: A medical student is reviewing dose-response curves of various experimental drugs. She is specifically interested in the different factors that cause the curve to shift in different directions. From her study, she plots the following graph (see image). She marks the blue curve for drug A, which acts optimally on a receptor. After drawing the second (green) curve for drug B, she discovers that more of drug B is required to produce the same response as drug A, although drug B can still achieve the same maximum effect. Which of the following terms best describes the activity of drug B in comparison to drug A?
- A. Decreased efficacy
- B. Increased affinity
- C. Higher potency
- D. Higher efficacy
- E. Lower potency (Correct Answer)
Area under the curve calculations Explanation: ***Lower potency***
- **Potency** refers to the amount of drug required to produce a given effect; if more of drug B is needed for the same response as drug A, it has lower potency.
- On a dose-response curve, **lower potency** is indicated by a rightward shift of the curve, meaning a higher dose is required to achieve any given effect.
*Decreased efficacy*
- **Efficacy** is the maximum effect a drug can produce, regardless of the dose.
- While drug B has a lower ability to produce a reaction (implying lower efficacy), the statement "more of the second drug B is required to produce the same response as the first one" specifically points to potency, not just the maximal effect.
*Increased affinity*
- **Affinity** describes how strongly a drug binds to its receptor.
- Increased affinity would generally lead to greater potency (less drug needed for an effect), which contradicts the scenario where more drug B is required.
*Higher potency*
- **Higher potency** would mean that less of drug B is required to produce the same effect as drug A, which is the opposite of what is described in the question.
- A drug with higher potency would cause the dose-response curve to shift to the left.
*Higher efficacy*
- **Higher efficacy** would mean drug B could produce a greater maximal effect than drug A, but the question states drug B has a "lower ability to produce a reaction" compared to drug A.
- The peak of the dose-response curve for drug B would be higher than drug A, which is not suggested by the description.
Area under the curve calculations US Medical PG Question 5: You are currently employed as a clinical researcher working on clinical trials of a new drug to be used for the treatment of Parkinson's disease. Currently, you have already determined the safe clinical dose of the drug in a healthy patient. You are in the phase of drug development where the drug is studied in patients with the target disease to determine its efficacy. Which of the following phases is this new drug currently in?
- A. Phase 4
- B. Phase 1
- C. Phase 2 (Correct Answer)
- D. Phase 0
- E. Phase 3
Area under the curve calculations Explanation: ***Phase 2***
- **Phase 2 trials** involve studying the drug in patients with the target disease to assess its **efficacy** and further evaluate safety, typically involving a few hundred patients.
- The question describes a stage after safe dosing in healthy patients (Phase 1) and before large-scale efficacy confirmation (Phase 3), focusing on efficacy in the target population.
*Phase 4*
- **Phase 4 trials** occur **after a drug has been approved** and marketed, monitoring long-term effects, optimal use, and rare side effects in a diverse patient population.
- This phase is conducted post-market approval, whereas the question describes a drug still in development prior to approval.
*Phase 1*
- **Phase 1 trials** primarily focus on determining the **safety and dosage** of a new drug in a **small group of healthy volunteers** (or sometimes patients with advanced disease if the drug is highly toxic).
- The question states that the safe clinical dose in a healthy patient has already been determined, indicating that Phase 1 has been completed.
*Phase 0*
- **Phase 0 trials** are exploratory, very early-stage studies designed to confirm that the drug reaches the target and acts as intended, typically involving a very small number of doses and participants.
- These trials are conducted much earlier in the development process, preceding the determination of safe clinical doses and large-scale efficacy studies.
*Phase 3*
- **Phase 3 trials** are large-scale studies involving hundreds to thousands of patients to confirm **efficacy**, monitor side effects, compare it to commonly used treatments, and collect information that will allow the drug to be used safely.
- While Phase 3 does assess efficacy, it follows Phase 2 and is typically conducted on a much larger scale before submitting for regulatory approval.
Area under the curve calculations US Medical PG Question 6: A researcher is investigating the effects of a new antihypertensive medication on renal physiology. She gives a subject a dose of the new medication, and she then collects plasma and urine samples. She finds the following: Hematocrit: 40%; Serum creatinine: 0.0125 mg/mL; Urine creatinine: 1.25 mg/mL. Urinary output is 1 mL/min. Renal blood flow is 1 L/min. Based on the above information and approximating that the creatinine clearance is equal to the GFR, what answer best approximates filtration fraction in this case?
- A. 10%
- B. 17% (Correct Answer)
- C. 33%
- D. 50%
- E. 25%
Area under the curve calculations Explanation: ***17%***
- First, calculate **GFR** using the creatinine clearance formula: GFR = (Urine creatinine × Urinary output) / Serum creatinine = (1.25 mg/mL × 1 mL/min) / 0.0125 mg/mL = **100 mL/min**.
- Next, calculate **Renal Plasma Flow (RPF)** from Renal Blood Flow (RBF) and Hematocrit: RPF = RBF × (1 - Hematocrit) = 1000 mL/min × (1 - 0.40) = **600 mL/min**.
- Finally, calculate **Filtration Fraction (FF)** = GFR / RPF = 100 mL/min / 600 mL/min = 0.1667 = **16.7%, which approximates to 17%**.
- This is the correct answer based on the physiological calculations and represents a normal filtration fraction.
*10%*
- This would correspond to a filtration fraction of 0.10, which would require either a GFR of 60 mL/min (lower than calculated) or an RPF of 1000 mL/min (higher than calculated).
- This value is too low given the provided parameters and doesn't match the calculation from the given data.
*25%*
- This value would suggest FF = 0.25, requiring a GFR of 150 mL/min with the calculated RPF of 600 mL/min.
- This is higher than the calculated GFR of 100 mL/min and doesn't match the given creatinine values.
*33%*
- This would imply FF = 0.33, requiring a GFR of approximately 200 mL/min with RPF of 600 mL/min.
- This is significantly higher than the calculated GFR and would represent an abnormally elevated filtration fraction.
*50%*
- A filtration fraction of 50% is unphysiologically high and would indicate severe pathology.
- This would require a GFR of 300 mL/min with the calculated RPF, which is impossible given the provided creatinine clearance data.
Area under the curve calculations US Medical PG Question 7: A 5-year-old boy undergoes MRI neuroimaging for the evaluation of worsening headaches and intermittent nausea upon awakening. He receives a bolus of intravenous thiopental for sedation during the procedure. Ten minutes after the MRI, the patient is awake and responsive. Which of the following pharmacological properties is most likely responsible for this patient's rapid recovery from this anesthetic agent?
- A. First-pass metabolism
- B. Redistribution (Correct Answer)
- C. Zero-order elimination
- D. Ion trapping
- E. Cytochrome P450 oxidation
Area under the curve calculations Explanation: ***Redistribution***
- Thiopental is a highly **lipid-soluble** drug that rapidly crosses the **blood-brain barrier**, leading to quick onset of action.
- The drug then rapidly **redistributes** from the brain to other highly perfused tissues (e.g., muscle, fat) and then less perfused tissues, causing a rapid decrease in drug concentration at the site of action and thus termination of the anesthetic effect.
*First-pass metabolism*
- This refers to the **metabolism of a drug** before it reaches systemic circulation, typically after oral administration, and does not explain the termination of action for an intravenously administered drug like thiopental.
- While thiopental is ultimately metabolized by the liver, this process is slower than redistribution and does not account for the **rapid awakening**.
*Zero-order elimination*
- **Zero-order elimination** occurs when a constant amount of drug is eliminated per unit of time, regardless of the drug's concentration, often seen with drug saturation of elimination pathways.
- Thiopental elimination follows **first-order kinetics** at therapeutic doses, meaning a constant fraction of the drug is eliminated per unit time, and this describes slower, overall elimination, not rapid recovery.
*Ion trapping*
- **Ion trapping** occurs when a drug accumulates in a compartment due to differences in pH across a membrane and the drug's pKa, leading to ionization and reduced ability to diffuse back.
- This mechanism is important for drug excretion or distribution into specific compartments (e.g., accumulation of basic drugs in acidic urine) but does not explain the **rapid termination of CNS effects** via redistribution.
*Cytochrome P450 oxidation*
- **Cytochrome P450 (CYP450) oxidation** is a major pathway for drug metabolism in the liver, which is responsible for the eventual elimination of thiopental from the body.
- While important for overall drug clearance, the rate of CYP450 oxidation is too slow to account for the **rapid awakening** seen after a single bolus dose of thiopental; redistribution is the primary factor for rapid recovery.
Area under the curve calculations US Medical PG Question 8: A 65-year-old man with a history of myocardial infarction is admitted to the hospital for treatment of atrial fibrillation with rapid ventricular response. He is 180 cm (5 ft 11 in) tall and weighs 80 kg (173 lb). He is given an intravenous bolus of 150 mg of amiodarone. After 20 minutes, the amiodarone plasma concentration is 2.5 mcg/mL. Amiodarone distributes in the body within minutes, and its elimination half-life after intravenous administration is 30 days. Which of the following values is closest to the volume of distribution of the administered drug?
- A. 60 L (Correct Answer)
- B. 80 L
- C. 150 L
- D. 17 L
- E. 10 L
Area under the curve calculations Explanation: ***60 L***
- The **volume of distribution (Vd)** is calculated using the formula: **Vd = Dose / Plasma Concentration**.
- Given: Dose = 150 mg (150,000 mcg), Plasma concentration = 2.5 mcg/mL
- Calculation: Vd = 150,000 mcg / 2.5 mcg/mL = 60,000 mL = **60 L**
- Note: This calculation represents a simplified scenario. In clinical practice, amiodarone has an extremely large volume of distribution (60-100 L/kg or ~4,800-8,000 L in this patient) due to extensive tissue distribution, but the question tests the ability to apply the basic pharmacokinetic formula.
*80 L*
- This value would result if the plasma concentration were 1.875 mcg/mL (150,000 mcg / 80,000 mL), not the given 2.5 mcg/mL.
- This represents a common calculation error when working with pharmacokinetic parameters.
*150 L*
- This value would require a plasma concentration of 1 mcg/mL (150,000 mcg / 150,000 mL), which is lower than the measured 2.5 mcg/mL.
- This error might occur if the dose value were confused with the volume of distribution.
*17 L*
- This value would be obtained with a plasma concentration of approximately 8.8 mcg/mL (150,000 mcg / 17,000 mL), significantly higher than the measured 2.5 mcg/mL.
- This represents a significant underestimation of Vd and would suggest limited drug distribution.
*10 L*
- This value would require a plasma concentration of 15 mcg/mL (150,000 mcg / 10,000 mL), which is 6-fold higher than the given 2.5 mcg/mL.
- Such a small Vd would suggest drug confined primarily to plasma, which is inappropriate for lipophilic drugs with extensive tissue distribution.
Area under the curve calculations US Medical PG Question 9: An experimental infusable drug, X729, is currently being studied to determine its pharmacokinetics. The drug was found to have a half life of 1.5 hours and is eliminated by first order kinetics. What is the minimum number of hours required to reach a steady state concentration of >90%?
- A. 6 (Correct Answer)
- B. 3
- C. 7.5
- D. 1.5
- E. 4.5
Area under the curve calculations Explanation: ***6***
- For a drug eliminated by **first-order kinetics**, approximately **4 to 5 half-lives** are required to reach **steady-state concentration**.
- To reach >90% of steady-state, at least **4 half-lives** are needed, where **93.75%** of the steady state is achieved.
- The time taken would be **4 half-lives × 1.5 hours/half-life = 6 hours**, making this the **minimum time** to exceed 90%.
*3*
- This represents only **2 half-lives** (2 × 1.5 hours = 3 hours), which would achieve roughly **75%** of the steady-state concentration.
- This is insufficient to reach >90% of the steady-state concentration.
*7.5*
- This time point represents **5 half-lives** (5 × 1.5 hours = 7.5 hours), which would achieve approximately **97%** of the steady-state concentration.
- While this does exceed 90%, the question asks for the **minimum** number of hours required, and 90% is already exceeded at 6 hours (4 half-lives).
*1.5*
- This is only **1 half-life**, which would achieve approximately **50%** of the steady-state concentration.
- This is far too early to reach a >90% steady-state concentration.
*4.5*
- This represents **3 half-lives** (3 × 1.5 hours = 4.5 hours), achieving approximately **87.5%** of the steady-state concentration.
- While close to 90%, it does not quite reach "greater than 90%".
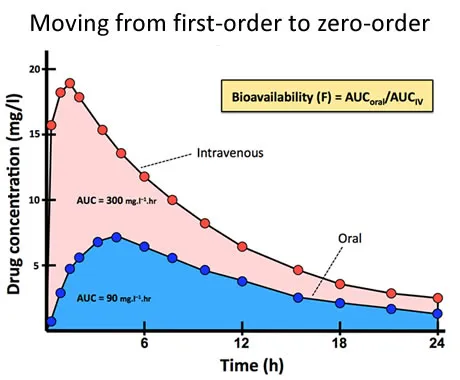
Area under the curve calculations US Medical PG Question 10: A researcher is investigating the behavior of two novel chemotherapeutic drugs that he believes will be effective against certain forms of lymphoma. In order to evaluate the safety of these drugs, this researcher measures the concentration and rate of elimination of each drug over time. A partial set of the results is provided below.
Time 1:
Concentration of Drug A: 4 mg/dl
Concentration of Drug B: 3 mg/dl
Elimination of Drug A: 1 mg/minute
Elimination of Drug B: 4 mg/minute
Time 2:
Concentration of Drug A: 2 mg/dl
Concentration of Drug B: 15 mg/dl
Elimination of Drug A: 0.5 mg/minute
Elimination of Drug B: 4 mg/minute
Which of the following statements correctly identifies the most likely relationship between the half-life of these two drugs?
- A. The half-life of drug A is always longer than that of drug B
- B. The half-life of both drug A and drug B are constant
- C. The half-life of both drug A and drug B are variable
- D. The half-life of drug A is variable but that of drug B is constant
- E. The half-life of drug A is constant but that of drug B is variable (Correct Answer)
Area under the curve calculations Explanation: ***The half-life of drug A is constant but that of drug B is variable***
- Drug A shows a **constant fraction** eliminated per unit time (1 mg/minute from 4 mg/dl, then 0.5 mg/minute from 2 mg/dl), indicating **first-order kinetics** and thus a constant half-life.
- Drug B's elimination rate remains constant (4 mg/minute) despite varying concentrations (3 mg/dl then 15 mg/dl), which suggests **zero-order kinetics** and a variable half-life dependent on concentration.
*The half-life of drug A is always longer than that of drug B*
- This statement is incorrect because Drug B exhibits **zero-order kinetics**, meaning its **half-life changes** with concentration, making a constant comparison invalid.
- At very high concentrations, Drug B's half-life could actually be longer than Drug A's if the elimination rate is slow relative to the large amount of drug.
*The half-life of both drug A and drug B are constant*
- This is incorrect because Drug B demonstrates **zero-order kinetics**, where the elimination rate is constant, but the **half-life is variable** and directly depends on the drug concentration.
- For zero-order kinetics, a constant amount of drug is eliminated per unit time, not a constant fraction, which causes the half-life to change.
*The half-life of both drug A and drug B are variable*
- This is incorrect because Drug A exhibits **first-order kinetics**, where a **constant proportion** of the drug is eliminated per unit time, resulting in a **constant half-life**.
- Its elimination rate is directly proportional to its concentration (1 mg/min from 4 mg/dl, 0.5 mg/min from 2 mg/dl), which defines first-order kinetics.
*The half-life of drug A is variable but that of drug B is constant*
- This statement is the opposite of what the data indicates for Drug A; Drug A's elimination is **proportional to its concentration**, signifying **first-order kinetics** and a constant half-life.
- Drug B's elimination rate is constant regardless of concentration, which points to **zero-order kinetics** and thus a variable half-life.
More Area under the curve calculations US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.