Sample size determination US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Sample size determination. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
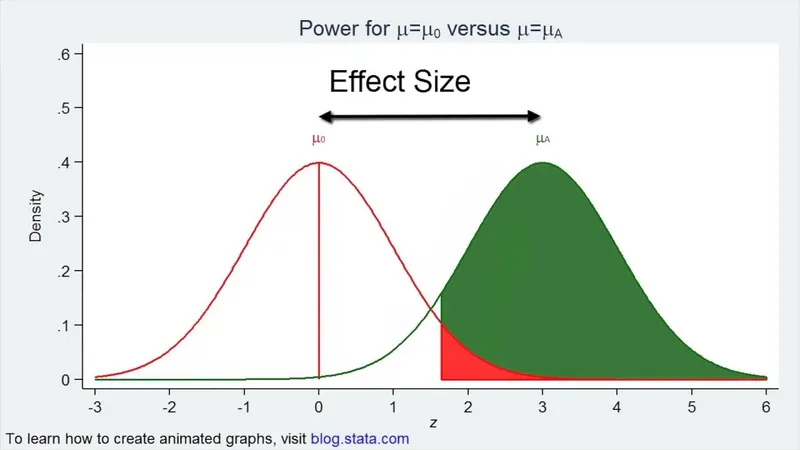
Sample size determination US Medical PG Question 1: You are reading through a recent article that reports significant decreases in all-cause mortality for patients with malignant melanoma following treatment with a novel biological infusion. Which of the following choices refers to the probability that a study will find a statistically significant difference when one truly does exist?
- A. Type II error
- B. Type I error
- C. Confidence interval
- D. p-value
- E. Power (Correct Answer)
Sample size determination Explanation: ***Power***
- **Power** is the probability that a study will correctly reject the null hypothesis when it is, in fact, false (i.e., will find a statistically significant difference when one truly exists).
- A study with high power minimizes the risk of a **Type II error** (failing to detect a real effect).
*Type II error*
- A **Type II error** (or **beta error**) occurs when a study fails to reject a false null hypothesis, meaning it concludes there is no significant difference when one actually exists.
- This is the **opposite** of what the question describes, which asks for the probability of *finding* a difference.
*Type I error*
- A **Type I error** (or **alpha error**) occurs when a study incorrectly rejects a true null hypothesis, concluding there is a significant difference when one does not actually exist.
- This relates to the **p-value** and the level of statistical significance (e.g., p < 0.05).
*Confidence interval*
- A **confidence interval** provides a range of values within which the true population parameter is likely to lie with a certain degree of confidence (e.g., 95%).
- It does not directly represent the probability of finding a statistically significant difference when one truly exists.
*p-value*
- The **p-value** is the probability of observing data as extreme as, or more extreme than, that obtained in the study, assuming the null hypothesis is true.
- It is used to determine statistical significance, but it is not the probability of detecting a true effect.
Sample size determination US Medical PG Question 2: A researcher is examining the relationship between socioeconomic status and IQ scores. The IQ scores of young American adults have historically been reported to be distributed normally with a mean of 100 and a standard deviation of 15. Initially, the researcher obtains a random sampling of 300 high school students from public schools nationwide and conducts IQ tests on all participants. Recently, the researcher received additional funding to enable an increase in sample size to 2,000 participants. Assuming that all other study conditions are held constant, which of the following is most likely to occur as a result of this additional funding?
- A. Increase in risk of systematic error
- B. Increase in range of the confidence interval
- C. Decrease in standard deviation
- D. Increase in probability of type II error
- E. Decrease in standard error of the mean (Correct Answer)
Sample size determination Explanation: ***Decrease in standard error of the mean***
- **Increasing the sample size** (n) leads to a **decrease in the standard error of the mean** (SEM), which is calculated as σ/√n.
- A smaller SEM indicates that our sample mean is a more **precise estimate** of the true population mean.
*Increase in risk of systematic error*
- **Systematic error** is related to flaws in study design or implementation and is not directly affected by an increase in sample size.
- A larger sample size generally helps in detecting a true effect if one exists, but does not inherently introduce or correct systematic bias.
*Increase in range of the confidence interval*
- An **increase in sample size** typically leads to a **narrower confidence interval**, not a wider one, because the standard error of the mean decreases.
- A narrower confidence interval implies greater precision in estimating the population parameter.
*Decrease in standard deviation*
- The **standard deviation** is a measure of the data's spread within a sample or population and is an intrinsic characteristic of the data itself.
- Increasing the sample size typically does not change the true standard deviation of the population; it only provides a **more accurate estimate** of it.
*Increase in probability of type II error*
- An **increase in sample size** generally leads to an **increase in statistical power**, which in turn **decreases the probability of a Type II error** (failing to reject a false null hypothesis).
- A larger sample makes it easier to detect a true difference or effect if one exists.
Sample size determination US Medical PG Question 3: A study is being conducted on depression using the Patient Health questionnaire (PHQ-9) survey data embedded within a popular social media network with a response size of 500,000 participants. The sample population of this study is approximately normal. The mean PHQ-9 score is 14, and the standard deviation is 4. How many participants have scores greater than 22?
- A. 175,000
- B. 17,500
- C. 160,000
- D. 12,500 (Correct Answer)
- E. 25,000
Sample size determination Explanation: ***12,500***
- To find the number of participants with scores greater than 22, first calculate the **z-score** for a score of 22: $Z = \frac{(X - \mu)}{\sigma} = \frac{(22 - 14)}{4} = 2$.
- A z-score of 2 means the score is **2 standard deviations above the mean**. Using the **empirical rule** for a normal distribution, approximately **2.5%** of the data falls beyond 2 standard deviations above the mean (5% total in both tails, so 2.5% in each tail).
- Therefore, $2.5\%$ of the total 500,000 participants is $0.025 \times 500,000 = 12,500$.
*175,000*
- This option would imply a much larger proportion of the population scoring above 22, inconsistent with the **normal distribution's properties** and the calculated z-score.
- It would correspond to a z-score closer to 0, indicating a score closer to the mean, not two standard deviations above it.
*17,500*
- This value represents **3.5%** of the total population ($17,500 / 500,000 = 0.035$).
- A proportion of 3.5% above the mean corresponds to a z-score that is not exactly 2, indicating an incorrect calculation or interpretation of the **normal distribution table**.
*160,000*
- This option represents a very large portion of the participants, roughly **32%** of the total population.
- This percentage would correspond to scores within one standard deviation of the mean, not scores 2 standard deviations above the mean as calculated.
*25,000*
- This value represents **5%** of the total population ($25,000 / 500,000 = 0.05$).
- A z-score greater than 2 corresponds to the far tail of the normal distribution, where only 2.5% of the data lies, not 5%. This would correspond to a z-score of approximately 1.65.
Sample size determination US Medical PG Question 4: You are currently employed as a clinical researcher working on clinical trials of a new drug to be used for the treatment of Parkinson's disease. Currently, you have already determined the safe clinical dose of the drug in a healthy patient. You are in the phase of drug development where the drug is studied in patients with the target disease to determine its efficacy. Which of the following phases is this new drug currently in?
- A. Phase 4
- B. Phase 1
- C. Phase 2 (Correct Answer)
- D. Phase 0
- E. Phase 3
Sample size determination Explanation: ***Phase 2***
- **Phase 2 trials** involve studying the drug in patients with the target disease to assess its **efficacy** and further evaluate safety, typically involving a few hundred patients.
- The question describes a stage after safe dosing in healthy patients (Phase 1) and before large-scale efficacy confirmation (Phase 3), focusing on efficacy in the target population.
*Phase 4*
- **Phase 4 trials** occur **after a drug has been approved** and marketed, monitoring long-term effects, optimal use, and rare side effects in a diverse patient population.
- This phase is conducted post-market approval, whereas the question describes a drug still in development prior to approval.
*Phase 1*
- **Phase 1 trials** primarily focus on determining the **safety and dosage** of a new drug in a **small group of healthy volunteers** (or sometimes patients with advanced disease if the drug is highly toxic).
- The question states that the safe clinical dose in a healthy patient has already been determined, indicating that Phase 1 has been completed.
*Phase 0*
- **Phase 0 trials** are exploratory, very early-stage studies designed to confirm that the drug reaches the target and acts as intended, typically involving a very small number of doses and participants.
- These trials are conducted much earlier in the development process, preceding the determination of safe clinical doses and large-scale efficacy studies.
*Phase 3*
- **Phase 3 trials** are large-scale studies involving hundreds to thousands of patients to confirm **efficacy**, monitor side effects, compare it to commonly used treatments, and collect information that will allow the drug to be used safely.
- While Phase 3 does assess efficacy, it follows Phase 2 and is typically conducted on a much larger scale before submitting for regulatory approval.
Sample size determination US Medical PG Question 5: In a randomized controlled trial studying a new treatment, the primary endpoint (mortality) occurred in 14.4% of the treatment group and 16.7% of the control group. Which of the following represents the number of patients needed to treat to save one life, based on the primary endpoint?
- A. 1/(0.144 - 0.167)
- B. 1/(0.167 - 0.144) (Correct Answer)
- C. 1/(0.300 - 0.267)
- D. 1/(0.267 - 0.300)
- E. 1/(0.136 - 0.118)
Sample size determination Explanation: ***1/(0.167 - 0.144)***
- The **Number Needed to Treat (NNT)** is calculated as **1 / Absolute Risk Reduction (ARR)**.
- The **Absolute Risk Reduction (ARR)** is the difference between the event rate in the control group (16.7%) and the event rate in the treatment group (14.4%), which is **0.167 - 0.144**.
*1/(0.144 - 0.167)*
- This calculation represents 1 divided by the **Absolute Risk Increase**, which would be relevant if the treatment increased mortality.
- The **NNT should always be a positive value**, indicating the number of patients to treat to prevent one adverse event.
*1/(0.300 - 0.267)*
- This option uses arbitrary numbers (0.300 and 0.267) that do not correspond to the given **mortality rates** in the problem.
- It does not reflect the correct calculation for **absolute risk reduction** based on the provided data.
*1/(0.267 - 0.300)*
- This option also uses arbitrary numbers not derived from the problem's data, and it would result in a **negative value** for the denominator.
- The difference between event rates of 0.267 and 0.300 is not present in the given information for this study.
*1/(0.136 - 0.118)*
- This calculation uses arbitrary numbers (0.136 and 0.118) that are not consistent with the reported **mortality rates** of 14.4% and 16.7%.
- These values do not represent the **Absolute Risk Reduction** required for calculating NNT in this specific scenario.
Sample size determination US Medical PG Question 6: A first-year medical student is conducting a summer project with his medical school's pediatrics department using adolescent IQ data from a database of 1,252 patients. He observes that the mean IQ of the dataset is 100. The standard deviation was calculated to be 10. Assuming that the values are normally distributed, approximately 87% of the measurements will fall in between which of the following limits?
- A. 85–115 (Correct Answer)
- B. 95–105
- C. 65–135
- D. 80–120
- E. 70–130
Sample size determination Explanation: ***85–115***
- For a **normal distribution**, approximately 87% of data falls within **±1.5 standard deviations** from the mean.
- With a mean of 100 and a standard deviation of 10, the range is 100 ± (1.5 * 10) = 100 ± 15, which gives **85–115**.
*95–105*
- This range represents **±0.5 standard deviations** from the mean (100 ± 5), which covers only about 38% of the data.
- This is a much narrower range and does not encompass 87% of the observations as required.
*65–135*
- This range represents **±3.5 standard deviations** from the mean (100 ± 35), which would cover over 99.9% of the data.
- Thus, this interval is too wide for 87% of the measurements.
*80–120*
- This range represents **±2 standard deviations** from the mean (100 ± 20), which covers approximately 95% of the data.
- While a common interval, it is wider than necessary for 87% of the data.
*70–130*
- This range represents **±3 standard deviations** from the mean (100 ± 30), which covers approximately 99.7% of the data.
- This interval is significantly wider than required to capture 87% of the data.
Sample size determination US Medical PG Question 7: A study seeks to investigate the therapeutic efficacy of treating asymptomatic subclinical hypothyroidism in preventing symptoms of hypothyroidism. The investigators found 300 asymptomatic patients with subclinical hypothyroidism, defined as serum thyroid-stimulating hormone (TSH) of 5 to 10 μU/mL with normal serum thyroxine (T4) levels. The patients were randomized to either thyroxine 75 μg daily or placebo. Both investigators and study subjects were blinded. Baseline patient characteristics were distributed similarly in the treatment and control group (p > 0.05). Participants' serum T4 and TSH levels and subjective quality of life were evaluated at a 3-week follow-up. No difference was found between the treatment and placebo groups. Which of the following is the most likely explanation for the results of this study?
- A. Observer effect
- B. Berkson bias
- C. Latency period (Correct Answer)
- D. Confounding bias
- E. Lead-time bias
Sample size determination Explanation: ***Latency period***
- A **latency period** refers to the time between exposure to a cause (e.g., treatment) and the manifestation of its effects (e.g., symptom improvement). The study's **3-week follow-up is too short** to observe the therapeutic benefits of thyroxine in subclinical hypothyroidism.
- Levothyroxine (T4) has a **half-life of approximately 7 days**, and it typically takes **6-8 weeks or longer** for steady-state levels to be achieved and for clinical symptoms to improve. The slow onset of action for thyroid hormone replacement and the gradual nature of symptom resolution mean a longer observation period (typically 3-6 months) is needed to assess efficacy in hypothyroidism.
- The null results likely reflect insufficient follow-up time rather than lack of treatment effect.
*Observer effect*
- The **observer effect**, or Hawthorne effect, occurs when subjects change their behavior because they know they are being observed. This study used **double-blinding** (both investigators and subjects), which effectively minimizes the observer effect.
- The primary issue here is the lack of observed therapeutic effect due to timing, not a change in behavior due to observation.
*Berkson bias*
- **Berkson bias** is a form of selection bias that arises in case-control studies conducted in hospitals, where the probability of being admitted to the hospital can be affected by both exposure and disease.
- This study is a **randomized controlled trial**, not a case-control study, and the selection of participants does not illustrate this specific bias.
*Confounding bias*
- **Confounding bias** occurs when an extraneous variable is associated with both the exposure and the outcome, distorting the observed relationship. The study states that **baseline patient characteristics were similarly distributed (p > 0.05)**, indicating successful randomization and minimization of confounding.
- While confounding is a common concern in observational studies, the RCT design and reported baseline similarities make it unlikely to be the primary explanation for the null results compared to an insufficient follow-up period.
*Lead-time bias*
- **Lead-time bias** is a form of detection bias where early detection of a disease through screening appears to prolong survival, even if the treatment does not change the course of the disease.
- This study is evaluating the **efficacy of treatment** in asymptomatic individuals with subclinical hypothyroidism, not the effect of screening on survival, making lead-time bias irrelevant to these results.
Sample size determination US Medical PG Question 8: In the study, all participants who were enrolled and randomly assigned to treatment with pulmharkimab were analyzed in the pulmharkimab group regardless of medication nonadherence or refusal of allocated treatment. A medical student reading the abstract is confused about why some participants assigned to pulmharkimab who did not adhere to the regimen were still analyzed as part of the pulmharkimab group. Which of the following best reflects the purpose of such an analysis strategy?
- A. To minimize type 2 errors
- B. To assess treatment efficacy more accurately
- C. To reduce selection bias (Correct Answer)
- D. To increase internal validity of study
- E. To increase sample size
Sample size determination Explanation: ***To reduce selection bias***
- Analyzing participants in their originally assigned groups, regardless of adherence, is known as **intention-to-treat (ITT) analysis**.
- This method helps **preserve randomization** and minimizes **selection bias** that could arise if participants who did not adhere to treatment were excluded or re-assigned.
- **This is the most direct and specific purpose** of ITT analysis - preventing systematic differences between groups caused by post-randomization exclusions.
*To minimize type 2 errors*
- While ITT analysis affects statistical power, its primary purpose is not specifically to minimize **type 2 errors** (false negatives).
- ITT analysis may sometimes *increase* the likelihood of a type 2 error by diluting the treatment effect due to non-adherence.
*To assess treatment efficacy more accurately*
- ITT analysis assesses the **effectiveness** of *assigning* a treatment in a real-world setting, rather than the pure biological **efficacy** of the treatment itself.
- Efficacy is better assessed by a **per-protocol analysis**, which only includes compliant participants.
- ITT provides a more **conservative** and **pragmatic** estimate of treatment effect.
*To increase internal validity of study*
- While ITT analysis does contribute to **internal validity** by maintaining randomization, this is a **broader, secondary benefit** rather than the primary purpose.
- Internal validity encompasses many aspects of study design; ITT specifically addresses **post-randomization bias prevention**.
- The more precise answer is that ITT reduces **selection bias**, which is one specific threat to internal validity.
- Many other design features also contribute to internal validity (blinding, standardized protocols, etc.), making this option less specific.
*To increase sample size*
- ITT analysis includes all randomized participants, so it maintains the initial **sample size** that was randomized.
- However, the primary purpose is to preserve the integrity of randomization and prevent bias, not simply to increase the number of participants in the final analysis.
Sample size determination US Medical PG Question 9: A randomized control double-blind study is conducted on the efficacy of 2 sulfonylureas. The study concluded that medication 1 was more efficacious in lowering fasting blood glucose than medication 2 (p ≤ 0.05; 95% CI: 14 [10-21]). Which of the following is true regarding a 95% confidence interval (CI)?
- A. If the same study were repeated multiple times, approximately 95% of the calculated confidence intervals would contain the true population parameter. (Correct Answer)
- B. The 95% confidence interval is the probability chosen by the researcher to be the threshold of statistical significance.
- C. When a 95% CI for the estimated difference between groups contains the value ‘0’, the results are significant.
- D. It represents the probability that chance would not produce the difference shown, 95% of the time.
- E. The study is adequately powered at the 95% confidence interval.
Sample size determination Explanation: ***If the same study were repeated multiple times, approximately 95% of the calculated confidence intervals would contain the true population parameter.***
- This statement accurately defines the **frequentist interpretation** of a confidence interval (CI). It reflects the long-run behavior of the CI over hypothetical repetitions of the study.
- A 95% CI means that if you were to repeat the experiment many times, 95% of the CIs calculated from those experiments would capture the **true underlying population parameter**.
*The 95% confidence interval is the probability chosen by the researcher to be the threshold of statistical significance.*
- The **alpha level (α)**, typically set at 0.05 (or 5%), is the threshold for statistical significance (p ≤ 0.05), representing the probability of a Type I error.
- The 95% confidence level (1-α) is related to statistical significance, but it is not the *threshold* itself; rather, it indicates the **reliability** of the interval estimate.
*When a 95% CI for the estimated difference between groups contains the value ‘0’, the results are significant.*
- If a 95% CI for the difference between groups **contains 0**, it implies that there is **no statistically significant difference** between the groups at the 0.05 alpha level.
- A statistically significant difference (p ≤ 0.05) would be indicated if the 95% CI **does NOT contain 0**, suggesting that the intervention had a real effect.
*It represents the probability that chance would not produce the difference shown, 95% of the time.*
- This statement misinterprets the meaning of a CI and probability. The chance of not producing the observed difference is typically addressed by the **p-value**, not directly by the CI in this manner.
- A CI provides a **range of plausible values** for the population parameter, not a probability about the role of chance in producing the observed difference.
*The study is adequately powered at the 95% confidence interval.*
- **Statistical power** is the probability of correctly rejecting a false null hypothesis, typically set at 80% or 90%. It is primarily determined by sample size, effect size, and alpha level.
- A 95% CI is a measure of the **precision** of an estimate, while power refers to the **ability of a study to detect an effect** if one exists. They are related but distinct concepts.
Sample size determination US Medical PG Question 10: A randomized controlled trial is conducted investigating the effects of different diagnostic imaging modalities on breast cancer mortality. 8,000 women are randomized to receive either conventional mammography or conventional mammography with breast MRI. The primary outcome is survival from the time of breast cancer diagnosis. The conventional mammography group has a median survival after diagnosis of 17.0 years. The MRI plus conventional mammography group has a median survival of 19.5 years. If this difference is statistically significant, which form of bias may be affecting the results?
- A. Recall bias
- B. Selection bias
- C. Misclassification bias
- D. Because this study is a randomized controlled trial, it is free of bias
- E. Lead-time bias (Correct Answer)
Sample size determination Explanation: ***Lead-time bias***
- This bias occurs when a screening test diagnoses a disease earlier, making **survival appear longer** even if the actual time of death is unchanged.
- In this scenario, adding **MRI** may detect breast cancer at an earlier, asymptomatic stage, artificially extending the apparent survival duration from diagnosis without necessarily changing the ultimate prognosis.
*Recall bias*
- **Recall bias** applies to retrospective studies where subjects are asked to recall past exposures, and those with the outcome are more likely to remember potential exposures.
- It's irrelevant here as this is a **prospective randomized controlled trial** studying objective survival outcomes, not subjective past recollections.
*Selection bias*
- **Selection bias** occurs when participants are not randomly assigned to groups, leading to systematic differences between the groups influencing the outcome.
- This study is a **randomized controlled trial**, which is designed to minimize selection bias by ensuring participants have an equal chance of being assigned to either treatment arm.
*Misclassification bias*
- **Misclassification bias** happens when either the exposure or the outcome is incorrectly categorized, leading to erroneous associations.
- This study uses objective diagnostic imaging and survival data, thus reducing the likelihood of **misclassification of diagnosis or survival status**.
*Because this study is a randomized controlled trial, it is free of bias*
- While **randomized controlled trials (RCTs)** are considered the **gold standard** for minimizing bias, they are not entirely immune to all forms of bias.
- **Lead-time bias**, for instance, can still occur in RCTs involving screening or early diagnosis, as seen in this example, and other biases like **information bias** or **reporting bias** can also arise.
More Sample size determination US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.