Primary vs secondary outcomes US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Primary vs secondary outcomes. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Primary vs secondary outcomes US Medical PG Question 1: A researcher is conducting a study to compare fracture risk in male patients above the age of 65 who received annual DEXA screening to peers who did not receive screening. He conducts a randomized controlled trial in 900 patients, with half of participants assigned to each experimental group. The researcher ultimately finds similar rates of fractures in the two groups. He then notices that he had forgotten to include 400 patients in his analysis. Including the additional participants in his analysis would most likely affect the study's results in which of the following ways?
- A. Wider confidence intervals of results
- B. Increased probability of committing a type II error
- C. Decreased significance level of results
- D. Increased external validity of results
- E. Increased probability of rejecting the null hypothesis when it is truly false (Correct Answer)
Primary vs secondary outcomes Explanation: ***Increased probability of rejecting the null hypothesis when it is truly false***
- Including more participants increases the **statistical power** of the study, making it more likely to detect a true effect if one exists.
- A higher sample size provides a more precise estimate of the population parameters, leading to a greater ability to **reject a false null hypothesis**.
*Wider confidence intervals of results*
- A larger sample size generally leads to **narrower confidence intervals**, as it reduces the standard error of the estimate.
- Narrower confidence intervals indicate **greater precision** in the estimation of the true population parameter.
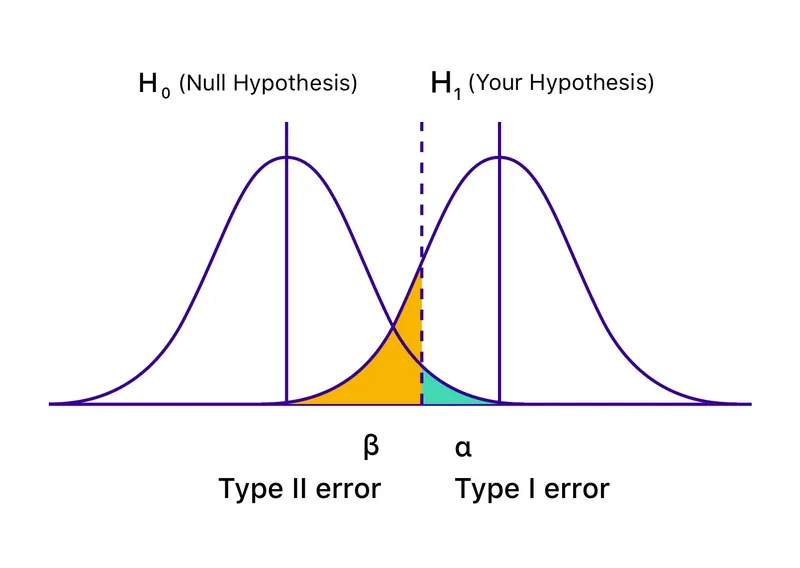
*Increased probability of committing a type II error*
- A **Type II error** (false negative) occurs when a study fails to reject a false null hypothesis.
- Increasing the sample size typically **reduces the probability of a Type II error** because it increases statistical power.
*Decreased significance level of results*
- The **significance level (alpha)** is a pre-determined threshold set by the researcher before the study begins, typically 0.05.
- It is independent of sample size and represents the **acceptable probability of committing a Type I error** (false positive).
*Increased external validity of results*
- **External validity** refers to the generalizability of findings to other populations, settings, or times.
- While a larger sample size can enhance the representativeness of the study population, external validity is primarily determined by the **sampling method** and the study's design context, not just sample size alone.
Primary vs secondary outcomes US Medical PG Question 2: A researcher is trying to determine whether a newly discovered substance X can be useful in promoting wound healing after surgery. She conducts this study by enrolling the next 100 patients that will be undergoing this surgery and separating them into 2 groups. She decides which patient will be in which group by using a random number generator. Subsequently, she prepares 1 set of syringes with the novel substance X and 1 set of syringes with a saline control. Both of these sets of syringes are unlabeled and the substances inside cannot be distinguished. She gives the surgeon performing the surgery 1 of the syringes and does not inform him nor the patient which syringe was used. After the study is complete, she analyzes all the data that was collected and performs statistical analysis. This study most likely provides which level of evidence for use of substance X?
- A. Level 3
- B. Level 1 (Correct Answer)
- C. Level 4
- D. Level 5
- E. Level 2
Primary vs secondary outcomes Explanation: ***Level 1***
- The study design described is a **randomized controlled trial (RCT)**, which is considered the **highest level of evidence (Level 1)** in the hierarchy of medical evidence.
- Key features like **randomization**, **control group**, and **blinding (double-blind)** help minimize bias and strengthen the validity of the findings.
*Level 2*
- Level 2 evidence typically comprises **well-designed controlled trials without randomization** (non-randomized controlled trials) or **high-quality cohort studies**.
- While strong, they do not possess the same level of internal validity as randomized controlled trials.
*Level 3*
- Level 3 evidence typically includes **case-control studies** or **cohort studies**, which are observational designs and carry a higher risk of bias compared to RCTs.
- These studies generally do not involve randomization or intervention assignment by the researchers.
*Level 4*
- Level 4 evidence is usually derived from **case series** or **poor quality cohort and case-control studies**.
- These studies provide descriptive information or investigate associations without strong control for confounding factors.
*Level 5*
- Level 5 evidence is the **lowest level of evidence**, consisting of **expert opinion** or **animal research/bench research**.
- This level lacks human clinical data or systematic investigative rigor needed for higher evidence levels.
Primary vs secondary outcomes US Medical PG Question 3: A pharmaceutical company conducts a randomized clinical trial to demonstrate that their new anticoagulant drug, Aclotsaban, prevents more thrombotic events following total knee arthroplasty than the current standard of care. A significant number of patients are lost to follow-up, and many fail to complete treatment according to the study arm to which they were assigned. Despite these protocol deviations, the results for the patients who completed the course of Aclotsaban are encouraging. Which of the following analytical approaches is most appropriate for the primary analysis to establish the efficacy of Aclotsaban?
- A. Intention-to-treat analysis (Correct Answer)
- B. Sub-group analysis
- C. Per-protocol analysis
- D. As-treated analysis
- E. Non-inferiority analysis
Primary vs secondary outcomes Explanation: ***Intention-to-treat analysis***
- **Intention-to-treat (ITT) analysis** is the gold standard for the **primary analysis in superiority trials** and includes all patients in the groups to which they were originally randomized, regardless of protocol deviations, loss to follow-up, or treatment discontinuation.
- ITT preserves **randomization balance**, prevents bias from selective dropout (patients may drop out due to adverse effects or lack of efficacy), and provides a **conservative, realistic estimate** of treatment effect in actual clinical practice.
- For **regulatory approval and establishing efficacy**, ITT is the most appropriate primary analysis method even when dropout rates are high, as it maintains the integrity of the randomized comparison.
*Per-protocol analysis*
- **Per-protocol analysis** includes only patients who completed the study exactly as planned without protocol deviations.
- While the encouraging results in completers are noted, per-protocol analysis can **introduce significant bias** by excluding patients who dropped out due to adverse events or lack of efficacy, potentially **overestimating treatment benefit**.
- Per-protocol is typically used as a **secondary/supportive analysis**, not the primary method for establishing superiority.
*As-treated analysis*
- **As-treated analysis** categorizes patients according to the treatment they actually received rather than their randomized assignment.
- This violates the principle of randomization and can introduce **confounding bias**, as actual treatment received may be influenced by prognostic factors.
*Sub-group analysis*
- **Sub-group analysis** evaluates treatment effects within specific patient subsets.
- This is **hypothesis-generating** rather than confirmatory and increases the risk of false-positive findings (multiple comparisons problem) unless pre-specified in the protocol.
*Non-inferiority analysis*
- **Non-inferiority analysis** tests whether a new treatment is not worse than control by more than a pre-specified margin.
- The goal here is to demonstrate **superiority** (better than standard care), not non-inferiority, making this approach inappropriate.
Primary vs secondary outcomes US Medical PG Question 4: An investigator is measuring the blood calcium level in a sample of female cross country runners and a control group of sedentary females. If she would like to compare the means of the two groups, which statistical test should she use?
- A. Chi-square test
- B. Linear regression
- C. t-test (Correct Answer)
- D. ANOVA (Analysis of Variance)
- E. F-test
Primary vs secondary outcomes Explanation: ***t-test***
- A **t-test** is appropriate for comparing the means of two independent groups, such as the blood calcium levels between runners and sedentary females.
- It assesses whether the observed difference between the two sample means is statistically significant or occurred by chance.
*Chi-square test*
- The **chi-square test** is used to analyze categorical data to determine if there is a significant association between two variables.
- It is not suitable for comparing continuous variables like blood calcium levels.
*Linear regression*
- **Linear regression** is used to model the relationship between a dependent variable (outcome) and one or more independent variables (predictors).
- It aims to predict the value of a variable based on the value of another, rather than comparing means between groups.
*ANOVA (Analysis of Variance)*
- **ANOVA** is used to compare the means of **three or more independent groups**.
- Since there are only two groups being compared in this scenario, a t-test is more specific and appropriate.
*F-test*
- The **F-test** is primarily used to compare the variances of two populations or to assess the overall significance of a regression model.
- While it is the basis for ANOVA, it is not the direct test for comparing the means of two groups.
Primary vs secondary outcomes US Medical PG Question 5: You conduct a medical research study to determine the screening efficacy of a novel serum marker for colon cancer. The study is divided into 2 subsets. In the first, there are 500 patients with colon cancer, of which 450 are found positive for the novel serum marker. In the second arm, there are 500 patients who do not have colon cancer, and only 10 are found positive for the novel serum marker. What is the overall sensitivity of this novel test?
- A. 450 / (450 + 10)
- B. 490 / (10 + 490)
- C. 490 / (50 + 490)
- D. 450 / (450 + 50) (Correct Answer)
- E. 490 / (450 + 490)
Primary vs secondary outcomes Explanation: ***450 / (450 + 50)***
- **Sensitivity** is defined as the proportion of actual positive cases that are correctly identified by the test.
- In this study, there are **500 patients with colon cancer** (actual positives), and **450 of them tested positive** for the marker, while **50 tested negative** (500 - 450 = 50). Therefore, sensitivity = 450 / (450 + 50) = 450/500 = 0.9 or 90%.
*450 / (450 + 10)*
- This formula represents **Positive Predictive Value (PPV)**, which is the probability that a person with a positive test result actually has the disease.
- It incorrectly uses the total number of **test positives** in the denominator (450 true positives + 10 false positives) instead of the total number of diseased individuals, which is needed for sensitivity.
*490 / (10 + 490)*
- This is actually the correct formula for **specificity**, not sensitivity.
- Specificity = TN / (FP + TN) = 490 / (10 + 490) = 490/500 = 0.98 or 98%, which measures the proportion of actual negative cases correctly identified.
- The question asks for sensitivity, not specificity.
*490 / (50 + 490)*
- This formula incorrectly mixes **true negatives (490)** with **false negatives (50)** in an attempt to calculate specificity.
- The correct specificity formula should use false positives (10), not false negatives (50), in the denominator: 490 / (10 + 490).
*490 / (450 + 490)*
- This calculation incorrectly combines **true negatives (490)** and **true positives (450)** in the denominator, which does not correspond to any standard epidemiological measure.
- Neither sensitivity nor specificity uses both true positives and true negatives in the denominator.
Primary vs secondary outcomes US Medical PG Question 6: A medical research study is beginning to evaluate the positive predictive value of a novel blood test for non-Hodgkin’s lymphoma. The diagnostic arm contains 700 patients with NHL, of which 400 tested positive for the novel blood test. In the control arm, 700 age-matched control patients are enrolled and 0 are found positive for the novel test. What is the PPV of this test?
- A. 400 / (400 + 0) (Correct Answer)
- B. 700 / (700 + 300)
- C. 400 / (400 + 300)
- D. 700 / (700 + 0)
- E. 700 / (400 + 400)
Primary vs secondary outcomes Explanation: ***400 / (400 + 0) = 1.0 or 100%***
- The **positive predictive value (PPV)** is calculated as **True Positives / (True Positives + False Positives)**.
- In this scenario, **True Positives (TP)** are the 400 patients with NHL who tested positive, and **False Positives (FP)** are 0, as no control patients tested positive.
- This gives a PPV of 400/400 = **1.0 or 100%**, indicating that all patients who tested positive actually had the disease.
*700 / (700 + 300)*
- This calculation does not align with the formula for PPV based on the given data.
- The denominator `(700+300)` suggests an incorrect combination of various patient groups.
*400 / (400 + 300)*
- The denominator `(400+300)` incorrectly includes 300, which is the number of **False Negatives** (patients with NHL who tested negative), not False Positives.
- PPV focuses on the proportion of true positives among all positive tests, not all diseased individuals.
*700 / (700 + 0)*
- This calculation incorrectly uses the total number of patients with NHL (700) as the numerator, rather than the number of positive test results in that group.
- The numerator should be the **True Positives** (400), not the total number of diseased individuals.
*700 / (400 + 400)*
- This calculation uses incorrect values for both the numerator and denominator, not corresponding to the PPV formula.
- The numerator 700 represents the total number of patients with the disease, not those who tested positive, and the denominator incorrectly sums up values that don't represent the proper PPV calculation.
Primary vs secondary outcomes US Medical PG Question 7: An academic medical center in the United States is approached by a pharmaceutical company to run a small clinical trial to test the effectiveness of its new drug, compound X. The company wants to know if the measured hemoglobin a1c (Hba1c) of patients with type 2 diabetes receiving metformin and compound X would be lower than that of control subjects receiving only metformin. After a year of study and data analysis, researchers conclude that the control and treatment groups did not differ significantly in their Hba1c levels.
However, parallel clinical trials in several other countries found that compound X led to a significant decrease in Hba1c. Interested in the discrepancy between these findings, the company funded a larger study in the United States, which confirmed that compound X decreased Hba1c levels. After compound X was approved by the FDA, and after several years of use in the general population, outcomes data confirmed that it effectively lowered Hba1c levels and increased overall survival. What term best describes the discrepant findings in the initial clinical trial run by institution A?
- A. Type I error
- B. Hawthorne effect
- C. Type II error (Correct Answer)
- D. Publication bias
- E. Confirmation bias
Primary vs secondary outcomes Explanation: ***Type II error***
- A **Type II error** occurs when a study fails to **reject a false null hypothesis**, meaning it concludes there is no significant difference or effect when one actually exists.
- In this case, the initial US trial incorrectly concluded that Compound X had no significant effect on HbA1c, while subsequent larger studies and real-world data proved it did.
*Type I error*
- A **Type I error** (alpha error) occurs when a study incorrectly **rejects a true null hypothesis**, concluding there is a significant difference or effect when there isn't.
- This scenario describes the opposite: the initial study failed to find an effect that genuinely existed, indicating a Type II error, not a Type I error.
*Hawthorne effect*
- The **Hawthorne effect** is a type of reactivity in which individuals modify an aspect of their behavior in response to their awareness of being observed.
- This effect does not explain the initial trial's failure to detect a real drug effect; rather, it relates to participants changing behavior due to study participation itself.
*Publication bias*
- **Publication bias** occurs when studies with positive or statistically significant results are more likely to be published than those with negative or non-significant results.
- While relevant to the literature as a whole, it doesn't explain the discrepancy in findings within a single drug's development where a real effect was initially missed.
*Confirmation bias*
- **Confirmation bias** is the tendency to search for, interpret, favor, and recall information in a way that confirms one's preexisting beliefs or hypotheses.
- This bias would likely lead researchers to *find* an effect if they expected one, or to disregard data that contradicts their beliefs, which is not what happened in the initial trial.
Primary vs secondary outcomes US Medical PG Question 8: In a randomized controlled trial studying a new treatment, the primary endpoint (mortality) occurred in 14.4% of the treatment group and 16.7% of the control group. Which of the following represents the number of patients needed to treat to save one life, based on the primary endpoint?
- A. 1/(0.144 - 0.167)
- B. 1/(0.167 - 0.144) (Correct Answer)
- C. 1/(0.300 - 0.267)
- D. 1/(0.267 - 0.300)
- E. 1/(0.136 - 0.118)
Primary vs secondary outcomes Explanation: ***1/(0.167 - 0.144)***
- The **Number Needed to Treat (NNT)** is calculated as **1 / Absolute Risk Reduction (ARR)**.
- The **Absolute Risk Reduction (ARR)** is the difference between the event rate in the control group (16.7%) and the event rate in the treatment group (14.4%), which is **0.167 - 0.144**.
*1/(0.144 - 0.167)*
- This calculation represents 1 divided by the **Absolute Risk Increase**, which would be relevant if the treatment increased mortality.
- The **NNT should always be a positive value**, indicating the number of patients to treat to prevent one adverse event.
*1/(0.300 - 0.267)*
- This option uses arbitrary numbers (0.300 and 0.267) that do not correspond to the given **mortality rates** in the problem.
- It does not reflect the correct calculation for **absolute risk reduction** based on the provided data.
*1/(0.267 - 0.300)*
- This option also uses arbitrary numbers not derived from the problem's data, and it would result in a **negative value** for the denominator.
- The difference between event rates of 0.267 and 0.300 is not present in the given information for this study.
*1/(0.136 - 0.118)*
- This calculation uses arbitrary numbers (0.136 and 0.118) that are not consistent with the reported **mortality rates** of 14.4% and 16.7%.
- These values do not represent the **Absolute Risk Reduction** required for calculating NNT in this specific scenario.
Primary vs secondary outcomes US Medical PG Question 9: You are reviewing raw data from a research study performed at your medical center examining the effectiveness of a novel AIDS screening examination. The study enrolled 250 patients with confirmed AIDS, and 240 of these patients demonstrated a positive screening examination. The control arm of the study enrolled 250 patients who do not have AIDS, and only 5 of these patients tested positive on the novel screening examination. What is the NPV of this novel test?
- A. 240 / (240 + 15)
- B. 240 / (240 + 5)
- C. 240 / (240 + 10)
- D. 245 / (245 + 10) (Correct Answer)
- E. 245 / (245 + 5)
Primary vs secondary outcomes Explanation: ***245 / (245 + 10)***
- The **negative predictive value (NPV)** is calculated as **true negatives (TN)** divided by the sum of **true negatives (TN)** and **false negatives (FN)**.
- In this study, there are 250 patients with AIDS; 240 tested positive (true positives, TP), meaning 10 tested negative (false negatives, FN = 250 - 240). There are 250 patients without AIDS; 5 tested positive (false positives, FP), meaning 245 tested negative (true negatives, TN = 250 - 5). Therefore, NPV = 245 / (245 + 10).
*240 / (240 + 15)*
- This calculation incorrectly uses the number of **true positives** (240) in the numerator and denominator, which is relevant for **positive predictive value (PPV)**, not NPV.
- The denominator `(240 + 15)` does not correspond to a valid sum for calculating NPV from the given data.
*240 / (240 + 5)*
- This calculation incorrectly uses **true positives** (240) in the numerator, which is not part of the NPV formula.
- The denominator `(240 + 5)` mixes true positives and false positives, which is incorrect for NPV.
*240 / (240 + 10)*
- This incorrectly places **true positives** (240) in the numerator instead of **true negatives**.
- The denominator `(240+10)` represents **true positives + false negatives**, which is related to sensitivity, not NPV.
*245 / (245 + 5)*
- This calculation correctly identifies **true negatives** (245) in the numerator but incorrectly uses **false positives** (5) in the denominator instead of **false negatives**.
- The denominator for NPV should be **true negatives + false negatives**, which is 245 + 10.
Primary vs secondary outcomes US Medical PG Question 10: You are reading through a recent article that reports significant decreases in all-cause mortality for patients with malignant melanoma following treatment with a novel biological infusion. Which of the following choices refers to the probability that a study will find a statistically significant difference when one truly does exist?
- A. Type II error
- B. Type I error
- C. Confidence interval
- D. p-value
- E. Power (Correct Answer)
Primary vs secondary outcomes Explanation: ***Power***
- **Power** is the probability that a study will correctly reject the null hypothesis when it is, in fact, false (i.e., will find a statistically significant difference when one truly exists).
- A study with high power minimizes the risk of a **Type II error** (failing to detect a real effect).
*Type II error*
- A **Type II error** (or **beta error**) occurs when a study fails to reject a false null hypothesis, meaning it concludes there is no significant difference when one actually exists.
- This is the **opposite** of what the question describes, which asks for the probability of *finding* a difference.
*Type I error*
- A **Type I error** (or **alpha error**) occurs when a study incorrectly rejects a true null hypothesis, concluding there is a significant difference when one does not actually exist.
- This relates to the **p-value** and the level of statistical significance (e.g., p < 0.05).
*Confidence interval*
- A **confidence interval** provides a range of values within which the true population parameter is likely to lie with a certain degree of confidence (e.g., 95%).
- It does not directly represent the probability of finding a statistically significant difference when one truly exists.
*p-value*
- The **p-value** is the probability of observing data as extreme as, or more extreme than, that obtained in the study, assuming the null hypothesis is true.
- It is used to determine statistical significance, but it is not the probability of detecting a true effect.
More Primary vs secondary outcomes US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.