Type I and Type II errors US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Type I and Type II errors. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Type I and Type II errors US Medical PG Question 1: A researcher is trying to determine whether a newly discovered substance X can be useful in promoting wound healing after surgery. She conducts this study by enrolling the next 100 patients that will be undergoing this surgery and separating them into 2 groups. She decides which patient will be in which group by using a random number generator. Subsequently, she prepares 1 set of syringes with the novel substance X and 1 set of syringes with a saline control. Both of these sets of syringes are unlabeled and the substances inside cannot be distinguished. She gives the surgeon performing the surgery 1 of the syringes and does not inform him nor the patient which syringe was used. After the study is complete, she analyzes all the data that was collected and performs statistical analysis. This study most likely provides which level of evidence for use of substance X?
- A. Level 3
- B. Level 1 (Correct Answer)
- C. Level 4
- D. Level 5
- E. Level 2
Type I and Type II errors Explanation: ***Level 1***
- The study design described is a **randomized controlled trial (RCT)**, which is considered the **highest level of evidence (Level 1)** in the hierarchy of medical evidence.
- Key features like **randomization**, **control group**, and **blinding (double-blind)** help minimize bias and strengthen the validity of the findings.
*Level 2*
- Level 2 evidence typically comprises **well-designed controlled trials without randomization** (non-randomized controlled trials) or **high-quality cohort studies**.
- While strong, they do not possess the same level of internal validity as randomized controlled trials.
*Level 3*
- Level 3 evidence typically includes **case-control studies** or **cohort studies**, which are observational designs and carry a higher risk of bias compared to RCTs.
- These studies generally do not involve randomization or intervention assignment by the researchers.
*Level 4*
- Level 4 evidence is usually derived from **case series** or **poor quality cohort and case-control studies**.
- These studies provide descriptive information or investigate associations without strong control for confounding factors.
*Level 5*
- Level 5 evidence is the **lowest level of evidence**, consisting of **expert opinion** or **animal research/bench research**.
- This level lacks human clinical data or systematic investigative rigor needed for higher evidence levels.
Type I and Type II errors US Medical PG Question 2: You are reading through a recent article that reports significant decreases in all-cause mortality for patients with malignant melanoma following treatment with a novel biological infusion. Which of the following choices refers to the probability that a study will find a statistically significant difference when one truly does exist?
- A. Type II error
- B. Type I error
- C. Confidence interval
- D. p-value
- E. Power (Correct Answer)
Type I and Type II errors Explanation: ***Power***
- **Power** is the probability that a study will correctly reject the null hypothesis when it is, in fact, false (i.e., will find a statistically significant difference when one truly exists).
- A study with high power minimizes the risk of a **Type II error** (failing to detect a real effect).
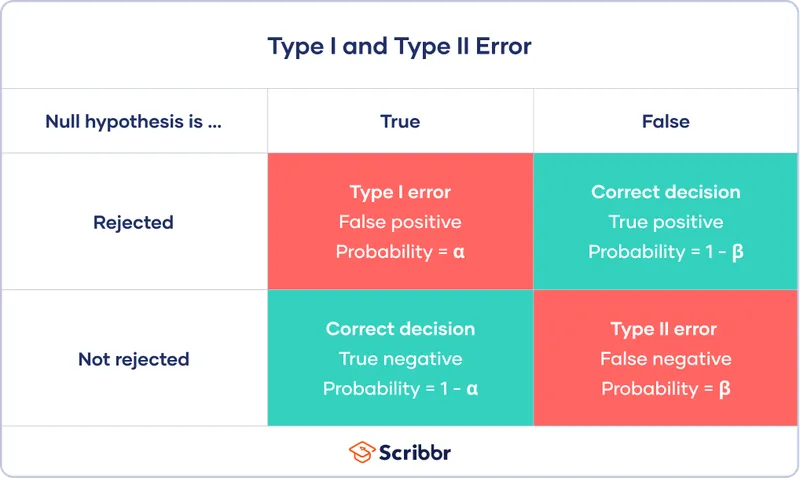
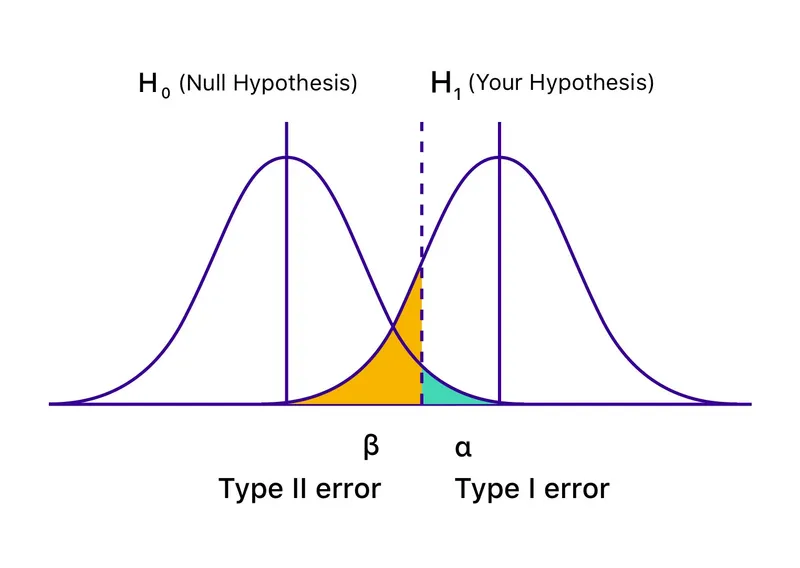
*Type II error*
- A **Type II error** (or **beta error**) occurs when a study fails to reject a false null hypothesis, meaning it concludes there is no significant difference when one actually exists.
- This is the **opposite** of what the question describes, which asks for the probability of *finding* a difference.
*Type I error*
- A **Type I error** (or **alpha error**) occurs when a study incorrectly rejects a true null hypothesis, concluding there is a significant difference when one does not actually exist.
- This relates to the **p-value** and the level of statistical significance (e.g., p < 0.05).
*Confidence interval*
- A **confidence interval** provides a range of values within which the true population parameter is likely to lie with a certain degree of confidence (e.g., 95%).
- It does not directly represent the probability of finding a statistically significant difference when one truly exists.
*p-value*
- The **p-value** is the probability of observing data as extreme as, or more extreme than, that obtained in the study, assuming the null hypothesis is true.
- It is used to determine statistical significance, but it is not the probability of detecting a true effect.
Type I and Type II errors US Medical PG Question 3: An 18-year-old male reports to his physician that he is having repeated episodes of a "racing heart beat". He believes these episodes are occurring completely at random. He is experiencing approximately 2 episodes each week, each lasting for only a few minutes. During the episodes he feels palpitations and shortness of breath, then nervous and uncomfortable, but these feelings resolve in a matter of minutes. He is otherwise well. Vital signs are as follows: T 98.8F, HR 60 bpm, BP 110/80 mmHg, RR 12. His resting EKG shows a short PR interval and a delta wave. What is the likely diagnosis?
- A. Atrioventricular reentrant tachycardia (Correct Answer)
- B. Paroxysmal atrial fibrillation
- C. Ventricular tachycardia
- D. Panic attacks
- E. Atrioventricular block, Mobitz Type II
Type I and Type II errors Explanation: ***Atrioventricular reentrant tachycardia***
- The patient's presentation with sudden onset, paroxysmal episodes of "racing heartbeat," shortness of breath, and nervousness in an otherwise healthy young male is highly suggestive of **supraventricular tachycardia (SVT)**.
- The **short PR interval and delta wave** on resting EKG are pathognomonic for **Wolff-Parkinson-White (WPW) syndrome**, which involves an accessory pathway (bundle of Kent) between the atria and ventricles.
- **Atrioventricular reentrant tachycardia (AVRT)** is the most common arrhythmia associated with WPW syndrome, where the reentrant circuit involves the accessory pathway, causing paroxysmal tachycardia episodes.
*Paroxysmal atrial fibrillation*
- While paroxysmal atrial fibrillation can cause a "racing heartbeat," it typically presents with an **irregularly irregular rhythm**, which is not suggested by the consistent episodes described.
- The presence of **delta waves on EKG** points specifically to an accessory pathway (WPW), not atrial fibrillation as the primary diagnosis.
- Note: Patients with WPW can develop atrial fibrillation, but it would conduct irregularly, not as the regular paroxysmal episodes described.
*Ventricular tachycardia*
- **Ventricular tachycardia (VT)** is a more serious arrhythmia, generally associated with structural heart disease or channelopathies, and typically presents with more severe symptoms like syncope or hemodynamic compromise.
- The **delta wave and short PR interval** indicate a supraventricular accessory pathway, not a ventricular origin of the arrhythmia.
- In a young, otherwise healthy individual with normal vital signs between episodes, VT is much less likely than AVRT.
*Panic attacks*
- While panic attacks can cause symptoms like palpitations and shortness of breath, they would not produce **EKG findings of delta waves and short PR interval**.
- The specific EKG findings indicate a **structural cardiac accessory pathway** rather than a purely psychological etiology.
- The description of consistent "racing heart beat" episodes with characteristic EKG changes confirms a primary cardiac arrhythmia (AVRT) rather than panic disorder.
*Atrioventricular block, Mobitz Type II*
- **Mobitz Type II AV block** is a bradyarrhythmia characterized by intermittent dropped QRS complexes following P waves, leading to a slow heart rate.
- This condition would cause **bradycardia and possible syncope**, not a "racing heart beat" or palpitations associated with tachycardia.
- The EKG findings of **short PR interval (not prolonged) and delta wave** are completely inconsistent with AV block.
Type I and Type II errors US Medical PG Question 4: A 55-year-old man with recurrent pneumonia comes to the physician for a follow-up examination one week after hospitalization for pneumonia. He feels well but still has a productive cough. He has smoked 1 pack of cigarettes daily for 5 years. His temperature is 36.9°C (98.4°F) and respirations are 20/min. Cardiopulmonary examination shows coarse crackles at the right lung base. Microscopic examination of a biopsy specimen of the right lower lung parenchyma shows proliferation of clustered, cuboidal, foamy-appearing cells. These cells are responsible for which of the following functions?
- A. Mucus secretion
- B. Cytokine release
- C. Lecithin production (Correct Answer)
- D. Toxin degradation
- E. Gas diffusion
Type I and Type II errors Explanation: ***Lecithin production***
- The description of **clustered, cuboidal, foamy-appearing cells** in the lung parenchyma strongly suggests **Type II pneumocytes**.
- **Type II pneumocytes** are primarily responsible for producing and secreting **pulmonary surfactant**, which is rich in **lecithin (phosphatidylcholine)**, to reduce surface tension in the alveoli.
*Mucus secretion*
- **Goblet cells** and **submucosal glands** in the airways are responsible for mucus secretion, not the alveolar cells described.
- Mucus functions to trap particles and pathogens, preventing them from reaching the alveoli.
*Cytokine release*
- While various lung cells, including macrophages and epithelial cells, can release cytokines in response to inflammation or infection, it is not the primary defining function of Type II pneumocytes.
- **Cytokine release** is a broad immune response, not specific to the unique morphology and function described.
*Toxin degradation*
- The liver and kidneys are the primary organs for **toxin degradation** and excretion, though some detoxification can occur in the lungs.
- This function is not characteristic of **Type II pneumocytes**, which are focused on surfactant production and alveolar repair.
*Gas diffusion*
- **Gas diffusion** primarily occurs across the **Type I pneumocytes** (squamous alveolar cells) and the capillary endothelial cells due to their thinness and large surface area.
- **Type II pneumocytes** are thicker and less involved in direct gas exchange.
Type I and Type II errors US Medical PG Question 5: An 18-month-old girl is brought to the pediatrician’s office for failure to thrive and developmental delay. The patient’s mother says she has not started speaking and is just now starting to pull herself up to standing position. Furthermore, her movement appears to be restricted. Physical examination reveals coarse facial features and restricted joint mobility. Laboratory studies show increased plasma levels of several enzymes. Which of the following is the underlying biochemical defect in this patient?
- A. Congenital lack of lysosomal formation
- B. Inappropriate protein targeting to endoplasmic reticulum
- C. Failure of mannose phosphorylation (Correct Answer)
- D. Inappropriate degradation of lysosomal enzymes
- E. Misfolding of nuclear proteins
Type I and Type II errors Explanation: ***Failure of mannose phosphorylation***
- The constellation of **failure to thrive**, **developmental delay**, **coarse facial features**, restricted joint mobility, and elevated plasma enzymes in an 18-month-old girl is highly suggestive of **I-cell disease** (mucolipidosis type II).
- **I-cell disease** is caused by the deficiency of **N-acetylglucosaminyl-1-phosphotransferase**, an enzyme responsible for phosphorylating mannose residues on lysosomal enzymes, which is crucial for proper targeting to the lysosome.
*Congenital lack of lysosomal formation*
- **Lysosomes** are present in this condition, but their enzymes are misdirected.
- A congenital lack of lysosomal formation would present with even more severe and widespread cellular dysfunction, possibly incompatible with life beyond early embryonic stages.
*Inappropriate protein targeting to endoplasmic reticulum*
- Proteins destined for the endoplasmic reticulum (ER) are typically targeted by an N-terminal signal peptide and then processed within the ER.
- While ER dysfunction can cause various disorders, the specific symptoms and enzyme elevations point away from a primary ER targeting defect related to lysosomal enzymes.
*Inappropriate degradation of lysosomal enzymes*
- In I-cell disease, lysosomal enzymes are synthesized but are **not properly targeted to the lysosomes**; instead, they are secreted into the bloodstream, leading to their elevated plasma levels.
- While some degradation might occur, the primary issue is mis-packaging and secretion, not increased degradation within the cell.
*Misfolding of nuclear proteins*
- Misfolding of nuclear proteins can lead to a variety of genetic disorders and cellular stress responses, but the clinical presentation, particularly the accumulation of undegraded material and elevated plasma lysosomal enzymes, is not characteristic of primary nuclear protein misfolding.
- The pathology in I-cell disease centers on lysosomal dysfunction rather than nuclear protein abnormalities.
Type I and Type II errors US Medical PG Question 6: A 40-year-old woman who works as a secretary presents to your office complaining of new pain and numbness in both of her hands. For the past few weeks, the sensation has occurred after long days of typing, but it now occasionally wakes her up from sleep. You do not note any deformities of her wrists or hands, but you are able to reproduce pain and numbness in the first three and a half digits by tapping the wrist. What is the best initial treatment for this patient's complaint?
- A. Local steroid injections
- B. Carpal tunnel release surgery
- C. Splinting (Correct Answer)
- D. A trial of gabapentin
- E. Short-acting benzodiazepines
Type I and Type II errors Explanation: ***Splinting***
- This patient's symptoms are highly suggestive of **carpal tunnel syndrome (CTS)**, given the **pain and numbness** in the distribution of the **median nerve** (first three and a half digits) that is exacerbated by repetitive wrist movements (typing) and reproduced by **Tinel's sign** (tapping the wrist).
- **Splinting** the wrist, especially at night, is the **first-line conservative treatment** for CTS, as it keeps the wrist in a neutral position, reducing pressure on the median nerve.
*Local steroid injections*
- While local steroid injections can provide **temporary relief** for CTS, they are typically considered if splinting and activity modification are unsuccessful.
- They are not the **initial treatment** of choice due to potential side effects and the less invasive nature of splinting.
*Carpal tunnel release surgery*
- **Carpal tunnel release surgery** is a definitive treatment for CTS but is reserved for cases that fail conservative management, show signs of **thenar atrophy**, or have objective evidence of severe nerve compression on **electromyography/nerve conduction studies**.
- It is an **invasive procedure** and not appropriate as a first-line intervention.
*A trial of gabapentin*
- **Gabapentin** is an anticonvulsant often used to treat **neuropathic pain**, but it is generally reserved for more generalized or refractory neuropathic conditions.
- It is not the primary treatment for localized nerve compression like CTS when less invasive and more targeted options are available.
*Short-acting benzodiazepines*
- **Benzodiazepines** are primarily used for anxiety, insomnia, or muscle spasms and have **no direct role** in treating the underlying nerve compression or symptoms of carpal tunnel syndrome.
- They do not address the pathology and carry risks of dependency.
Type I and Type II errors US Medical PG Question 7: A 63-year-old man with alpha-1-antitrypsin deficiency is brought to the emergency department 1 hour after his daughter found him unresponsive. Despite appropriate care, the patient dies. At autopsy, examination of the lungs shows enlargement of the airspaces in the respiratory bronchioles and alveoli. Enzymatic activity of which of the following cells is the most likely cause of these findings?
- A. Alveolar macrophages (Correct Answer)
- B. Ciliated bronchiolar epithelial cells
- C. Elastic fibers in alveolar septa
- D. Type I pneumocytes
- E. Alveolar septal cells
Type I and Type II errors Explanation: ***Alveolar macrophages***
- In **alpha-1-antitrypsin deficiency**, alveolar macrophages (and neutrophils) release **elastase**, which is normally inhibited by alpha-1-antitrypsin.
- Unchecked elastase activity from alveolar macrophages leads to the **destruction of elastic fibers** in the alveolar walls, causing emphysema with characteristic **panacinar** distribution (worse in lower lobes).
- This results in enlargement of airspaces distal to terminal bronchioles.
*Ciliated bronchiolar epithelial cells*
- These cells are primarily involved in **mucociliary clearance** and do not produce proteolytic enzymes that degrade elastic tissue.
- Their dysfunction would lead to impaired mucus clearance and increased susceptibility to infections, but not emphysema.
*Elastic fibers in alveolar septa*
- Elastic fibers are **extracellular matrix components**, not cells.
- While their destruction is the pathological mechanism of emphysema, they do not have enzymatic activity.
*Type I pneumocytes*
- **Type I pneumocytes** form the structural lining of the alveoli and are primarily involved in gas exchange.
- They do not produce elastase or other proteolytic enzymes responsible for tissue destruction in emphysema.
*Alveolar septal cells*
- This term broadly refers to structural cells including Type I and Type II pneumocytes.
- While these cells may be damaged secondarily in emphysema, they do not produce the elastase responsible for elastic fiber destruction.
Type I and Type II errors US Medical PG Question 8: A 55-year-old woman presents with pain in both hands and wrists for several years. It is associated with morning stiffness that lasts for almost an hour. She has a blood pressure of 124/76 mm Hg, heart rate of 71/min, and respiratory rate of 14/min. Physical examination reveals tenderness and swelling in both hands and wrists. Laboratory investigations reveal the presence of anti-cyclic citrullinated peptide. Which of the following immune-mediated processes is responsible for this patient’s condition?
- A. Self-tolerance
- B. Type IV hypersensitivity
- C. IgE-mediated immune responses only
- D. Both type II and III hypersensitivities
- E. Type III hypersensitivity (Correct Answer)
Type I and Type II errors Explanation: ***Type III hypersensitivity***
- Rheumatoid arthritis (RA), suggested by **symmetric joint pain**, **morning stiffness >1 hour**, and **positive anti-CCP antibodies**, is primarily mediated by **Type III hypersensitivity** (immune complex-mediated).
- **Immune complexes** (rheumatoid factor-IgG complexes, anti-CCP complexes) deposit in the **synovium**, activate **complement**, and recruit inflammatory cells causing **chronic synovitis** and joint destruction.
- Note: Type IV hypersensitivity (T cell-mediated) also contributes significantly to RA pathogenesis, though this option is not provided.
*Self-tolerance*
- **Self-tolerance** is the immune system's ability to recognize and not attack self-antigens.
- RA represents a **breakdown of self-tolerance** (an autoimmune disease), not a mechanism of tissue damage itself.
*Type IV hypersensitivity*
- **Type IV hypersensitivity** (delayed-type, T cell-mediated) does play an important role in RA pathogenesis, with CD4+ T cells driving chronic inflammation.
- However, the **primary mechanism** involves immune complex deposition (Type III), making Type III the more complete answer when Type IV is not combined with it.
*IgE-mediated immune responses only*
- **IgE-mediated responses** (Type I hypersensitivity) cause **allergic reactions** like anaphylaxis, asthma, and hay fever.
- This involves IgE binding to mast cells/basophils with histamine release, which is **not characteristic of RA**.
*Both type II and III hypersensitivities*
- While **Type III hypersensitivity** is central to RA, **Type II hypersensitivity** (antibody-mediated cytotoxicity against cell surface antigens) is **not a primary mechanism** in RA.
- Type II occurs in diseases like Goodpasture syndrome, Graves' disease, and myasthenia gravis, where antibodies directly target cell surface receptors or tissue antigens.
- In RA, autoantibodies (RF, anti-CCP) primarily form **immune complexes** (Type III), not direct cell targeting (Type II).
Type I and Type II errors US Medical PG Question 9: A 33-year-old man presents with yellowing of the eyes. He says symptoms onset acutely 3 days ago and have not improved. He says he has had similar episodes for the past 10 years. Each episode is self-limited, lasting no more than 3–5 days. The patient denies any recent history of nausea, weight loss, abdominal pain, light-colored stools, dark urine, or pruritus. Current medications are herbal supplements and a multivitamin. The patient is afebrile and vital signs are within normal limits. His BMI is 32 kg/m2. Physical exam is unremarkable. Laboratory findings are significant for the following:
Total bilirubin 3 mg/dL
Direct bilirubin 0.2 mg/dL
AST/ALT/Alkaline phosphatase Normal
Hematocrit/lactate dehydrogenase (LDH)/haptoglobin Normal
Which of the following is the most likely diagnosis in this patient?
- A. Cholelithiasis
- B. Gilbert’s syndrome (Correct Answer)
- C. Medication-induced hemolysis
- D. Crigler-Najjar syndrome type 1
- E. Dubin-Johnson syndrome
Type I and Type II errors Explanation: ***Gilbert’s syndrome***
- The patient's history of **recurrent, self-limited episodes of jaundice** (yellowing of the eyes) with normal liver enzymes and a predominance of **unconjugated (indirect) bilirubin** (3 mg/dL total, 0.2 mg/dL direct) is characteristic of Gilbert's syndrome.
- This benign genetic condition is caused by a partial deficiency of **UGT1A1 enzyme**, leading to impaired bilirubin conjugation, especially during stress, fasting, or illness.
*Cholelithiasis*
- **Cholelithiasis** typically presents with biliary colic or complications like **obstructive jaundice**, characterized by elevated direct bilirubin, alkaline phosphatase, and often abdominal pain, which are absent here.
- The absence of dark urine, light-colored stools, and pruritus further argues against biliary obstruction.
*Medication-induced hemolysis*
- **Hemolysis** would lead to elevated indirect bilirubin, but also an increase in **LDH** and a decrease in **haptoglobin**, along with anemia, none of which are present in this patient.
- The patient denies current medications that are known to cause hemolysis (only herbal supplements and multivitamins).
*Crigler-Najjar syndrome type 1*
- **Crigler-Najjar syndrome type 1** is a much more severe condition with a complete absence of UGT1A1 activity, resulting in **profoundly elevated indirect bilirubin** (often >20 mg/dL) and neurological complications (kernicterus) typically manifesting in infancy.
- The patient's milder, intermittent symptoms and normal neurological status rule out this diagnosis.
*Dubin-Johnson syndrome*
- **Dubin-Johnson syndrome** is characterized by **impaired excretion of conjugated (direct) bilirubin** into the bile, leading to predominantly elevated direct bilirubin and dark urine, which are not seen in this patient.
- The liver may appear dark on biopsy due to impaired excretion of epinephrine metabolites.
Type I and Type II errors US Medical PG Question 10: A 52-year-old man is seen by his endocrinologist for routine followup of his type 2 diabetes. Although he has previously been on a number of medication regimens, his A1C has remained significantly elevated. In order to try to better control his glucose level, the endocrinologist prescribes a new medication. He explains that this new medication works by blocking the ability of his kidneys to reabsorb glucose and therefore causes glucose wasting in the urine. Which of the following medications has this mechanism of action?
- A. Canagliflozin (Correct Answer)
- B. Acarbose
- C. Metformin
- D. Glyburide
- E. Exenatide
Type I and Type II errors Explanation: ***Canagliflozin***
- **Canagliflozin** is an **SGLT2 inhibitor** that works by blocking the reabsorption of glucose in the renal tubules, leading to glucose excretion in the urine.
- This mechanism of action directly matches the description provided: "blocking the ability of his kidneys to reabsorb glucose and therefore causes glucose wasting in the urine."
*Acarbose*
- **Acarbose** is an **alpha-glucosidase inhibitor** that delays the digestion and absorption of carbohydrates in the small intestine.
- Its primary action is in the gastrointestinal tract, not by directly affecting renal glucose reabsorption.
*Metformin*
- **Metformin** is a **biguanide** that primarily works by decreasing hepatic glucose production and improving insulin sensitivity.
- It does not directly affect the kidney's ability to reabsorb glucose.
*Glyburide*
- **Glyburide** is a **sulfonylurea** that stimulates insulin secretion from pancreatic beta cells.
- Its mechanism involves increasing insulin release, independent of renal glucose handling.
*Exenatide*
- **Exenatide** is a **GLP-1 receptor agonist** that enhances glucose-dependent insulin secretion, suppresses glucagon secretion, slows gastric emptying, and promotes satiety.
- Its actions are mainly related to insulin and glucagon regulation, not direct renal glucose filtration.
More Type I and Type II errors US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.