Statistical power definition US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Statistical power definition. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Statistical power definition US Medical PG Question 1: A research team develops a new monoclonal antibody checkpoint inhibitor for advanced melanoma that has shown promise in animal studies as well as high efficacy and low toxicity in early phase human clinical trials. The research team would now like to compare this drug to existing standard of care immunotherapy for advanced melanoma. The research team decides to conduct a non-randomized study where the novel drug will be offered to patients who are deemed to be at risk for toxicity with the current standard of care immunotherapy, while patients without such risk factors will receive the standard treatment. Which of the following best describes the level of evidence that this study can offer?
- A. Level 1
- B. Level 3 (Correct Answer)
- C. Level 5
- D. Level 4
- E. Level 2
Statistical power definition Explanation: ***Level 3***
- A **non-randomized controlled trial** like the one described, where patient assignment to treatment groups is based on specific characteristics (risk of toxicity), falls into Level 3 evidence.
- This level typically includes **non-randomized controlled trials** and **well-designed cohort studies** with comparison groups, which are prone to selection bias and confounding.
- The study compares two treatments but lacks randomization, making it Level 3 evidence.
*Level 1*
- Level 1 evidence is the **highest level of evidence**, derived from **systematic reviews and meta-analyses** of multiple well-designed randomized controlled trials or large, high-quality randomized controlled trials.
- The described study is explicitly stated as non-randomized, ruling out Level 1.
*Level 2*
- Level 2 evidence involves at least one **well-designed randomized controlled trial** (RCT) or **systematic reviews** of randomized trials.
- The current study is *non-randomized*, which means it cannot be classified as Level 2 evidence, as randomization is a key criterion for this level.
*Level 4*
- Level 4 evidence includes **case series**, **case-control studies**, and **poorly designed cohort or case-control studies**.
- While the study is non-randomized, it is a controlled comparative trial rather than a case series or retrospective case-control study, placing it at Level 3.
*Level 5*
- Level 5 evidence is the **lowest level of evidence**, typically consisting of **expert opinion** without explicit critical appraisal, or based on physiology, bench research, or animal studies.
- While the drug was initially tested in animal studies, the current human comparative study offers a higher level of evidence than expert opinion or preclinical data.
Statistical power definition US Medical PG Question 2: A researcher is trying to determine whether a newly discovered substance X can be useful in promoting wound healing after surgery. She conducts this study by enrolling the next 100 patients that will be undergoing this surgery and separating them into 2 groups. She decides which patient will be in which group by using a random number generator. Subsequently, she prepares 1 set of syringes with the novel substance X and 1 set of syringes with a saline control. Both of these sets of syringes are unlabeled and the substances inside cannot be distinguished. She gives the surgeon performing the surgery 1 of the syringes and does not inform him nor the patient which syringe was used. After the study is complete, she analyzes all the data that was collected and performs statistical analysis. This study most likely provides which level of evidence for use of substance X?
- A. Level 3
- B. Level 1 (Correct Answer)
- C. Level 4
- D. Level 5
- E. Level 2
Statistical power definition Explanation: ***Level 1***
- The study design described is a **randomized controlled trial (RCT)**, which is considered the **highest level of evidence (Level 1)** in the hierarchy of medical evidence.
- Key features like **randomization**, **control group**, and **blinding (double-blind)** help minimize bias and strengthen the validity of the findings.
*Level 2*
- Level 2 evidence typically comprises **well-designed controlled trials without randomization** (non-randomized controlled trials) or **high-quality cohort studies**.
- While strong, they do not possess the same level of internal validity as randomized controlled trials.
*Level 3*
- Level 3 evidence typically includes **case-control studies** or **cohort studies**, which are observational designs and carry a higher risk of bias compared to RCTs.
- These studies generally do not involve randomization or intervention assignment by the researchers.
*Level 4*
- Level 4 evidence is usually derived from **case series** or **poor quality cohort and case-control studies**.
- These studies provide descriptive information or investigate associations without strong control for confounding factors.
*Level 5*
- Level 5 evidence is the **lowest level of evidence**, consisting of **expert opinion** or **animal research/bench research**.
- This level lacks human clinical data or systematic investigative rigor needed for higher evidence levels.
Statistical power definition US Medical PG Question 3: An investigator is measuring the blood calcium level in a sample of female cross country runners and a control group of sedentary females. If she would like to compare the means of the two groups, which statistical test should she use?
- A. Chi-square test
- B. Linear regression
- C. t-test (Correct Answer)
- D. ANOVA (Analysis of Variance)
- E. F-test
Statistical power definition Explanation: ***t-test***
- A **t-test** is appropriate for comparing the means of two independent groups, such as the blood calcium levels between runners and sedentary females.
- It assesses whether the observed difference between the two sample means is statistically significant or occurred by chance.
*Chi-square test*
- The **chi-square test** is used to analyze categorical data to determine if there is a significant association between two variables.
- It is not suitable for comparing continuous variables like blood calcium levels.
*Linear regression*
- **Linear regression** is used to model the relationship between a dependent variable (outcome) and one or more independent variables (predictors).
- It aims to predict the value of a variable based on the value of another, rather than comparing means between groups.
*ANOVA (Analysis of Variance)*
- **ANOVA** is used to compare the means of **three or more independent groups**.
- Since there are only two groups being compared in this scenario, a t-test is more specific and appropriate.
*F-test*
- The **F-test** is primarily used to compare the variances of two populations or to assess the overall significance of a regression model.
- While it is the basis for ANOVA, it is not the direct test for comparing the means of two groups.
Statistical power definition US Medical PG Question 4: A researcher is examining the relationship between socioeconomic status and IQ scores. The IQ scores of young American adults have historically been reported to be distributed normally with a mean of 100 and a standard deviation of 15. Initially, the researcher obtains a random sampling of 300 high school students from public schools nationwide and conducts IQ tests on all participants. Recently, the researcher received additional funding to enable an increase in sample size to 2,000 participants. Assuming that all other study conditions are held constant, which of the following is most likely to occur as a result of this additional funding?
- A. Increase in risk of systematic error
- B. Increase in range of the confidence interval
- C. Decrease in standard deviation
- D. Increase in probability of type II error
- E. Decrease in standard error of the mean (Correct Answer)
Statistical power definition Explanation: ***Decrease in standard error of the mean***
- **Increasing the sample size** (n) leads to a **decrease in the standard error of the mean** (SEM), which is calculated as σ/√n.
- A smaller SEM indicates that our sample mean is a more **precise estimate** of the true population mean.
*Increase in risk of systematic error*
- **Systematic error** is related to flaws in study design or implementation and is not directly affected by an increase in sample size.
- A larger sample size generally helps in detecting a true effect if one exists, but does not inherently introduce or correct systematic bias.
*Increase in range of the confidence interval*
- An **increase in sample size** typically leads to a **narrower confidence interval**, not a wider one, because the standard error of the mean decreases.
- A narrower confidence interval implies greater precision in estimating the population parameter.
*Decrease in standard deviation*
- The **standard deviation** is a measure of the data's spread within a sample or population and is an intrinsic characteristic of the data itself.
- Increasing the sample size typically does not change the true standard deviation of the population; it only provides a **more accurate estimate** of it.
*Increase in probability of type II error*
- An **increase in sample size** generally leads to an **increase in statistical power**, which in turn **decreases the probability of a Type II error** (failing to reject a false null hypothesis).
- A larger sample makes it easier to detect a true difference or effect if one exists.
Statistical power definition US Medical PG Question 5: A pharmaceutical corporation is developing a research study to evaluate a novel blood test to screen for breast cancer. They enrolled 800 patients in the study, half of which have breast cancer. The remaining enrolled patients are age-matched controls who do not have the disease. Of those in the diseased arm, 330 are found positive for the test. Of the patients in the control arm, only 30 are found positive. What is this test’s sensitivity?
- A. 330 / (330 + 30)
- B. 330 / (330 + 70) (Correct Answer)
- C. 370 / (30 + 370)
- D. 370 / (70 + 370)
- E. 330 / (400 + 400)
Statistical power definition Explanation: ***330 / (330 + 70)***
- **Sensitivity** measures the proportion of actual **positives** that are correctly identified as such.
- In this study, there are **400 diseased patients** (half of 800). Of these, 330 tested positive (true positives), meaning 70 tested negative (false negatives). So sensitivity is **330 / (330 + 70)**.
*330 / (330 + 30)*
- This calculation represents the **positive predictive value**, which is the probability that subjects with a positive screening test truly have the disease. It uses **true positives / (true positives + false positives)**.
- It does not correctly calculate **sensitivity**, which requires knowing the total number of diseased individuals.
*370 / (30 + 370)*
- This expression is attempting to calculate **specificity**, which is the proportion of actual negatives that are correctly identified. It would be **true negatives / (true negatives + false positives)**.
- However, the numbers used are incorrect for specificity in this context given the data provided.
*370 / (70 + 370)*
- This formula is an incorrect combination of values and does not represent any standard epidemiological measure like **sensitivity** or **specificity**.
- It is attempting to combine false negatives (70) and true negatives (370 from control arm) in a non-standard way.
*330 / (400 + 400)*
- This calculation attempts to divide true positives by the total study population (800 patients).
- This metric represents the **prevalence of true positives within the entire study cohort**, not the test's **sensitivity**.
Statistical power definition US Medical PG Question 6: You are currently employed as a clinical researcher working on clinical trials of a new drug to be used for the treatment of Parkinson's disease. Currently, you have already determined the safe clinical dose of the drug in a healthy patient. You are in the phase of drug development where the drug is studied in patients with the target disease to determine its efficacy. Which of the following phases is this new drug currently in?
- A. Phase 4
- B. Phase 1
- C. Phase 2 (Correct Answer)
- D. Phase 0
- E. Phase 3
Statistical power definition Explanation: ***Phase 2***
- **Phase 2 trials** involve studying the drug in patients with the target disease to assess its **efficacy** and further evaluate safety, typically involving a few hundred patients.
- The question describes a stage after safe dosing in healthy patients (Phase 1) and before large-scale efficacy confirmation (Phase 3), focusing on efficacy in the target population.
*Phase 4*
- **Phase 4 trials** occur **after a drug has been approved** and marketed, monitoring long-term effects, optimal use, and rare side effects in a diverse patient population.
- This phase is conducted post-market approval, whereas the question describes a drug still in development prior to approval.
*Phase 1*
- **Phase 1 trials** primarily focus on determining the **safety and dosage** of a new drug in a **small group of healthy volunteers** (or sometimes patients with advanced disease if the drug is highly toxic).
- The question states that the safe clinical dose in a healthy patient has already been determined, indicating that Phase 1 has been completed.
*Phase 0*
- **Phase 0 trials** are exploratory, very early-stage studies designed to confirm that the drug reaches the target and acts as intended, typically involving a very small number of doses and participants.
- These trials are conducted much earlier in the development process, preceding the determination of safe clinical doses and large-scale efficacy studies.
*Phase 3*
- **Phase 3 trials** are large-scale studies involving hundreds to thousands of patients to confirm **efficacy**, monitor side effects, compare it to commonly used treatments, and collect information that will allow the drug to be used safely.
- While Phase 3 does assess efficacy, it follows Phase 2 and is typically conducted on a much larger scale before submitting for regulatory approval.
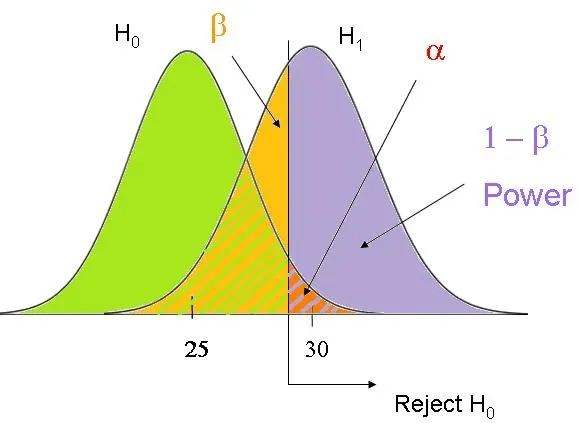
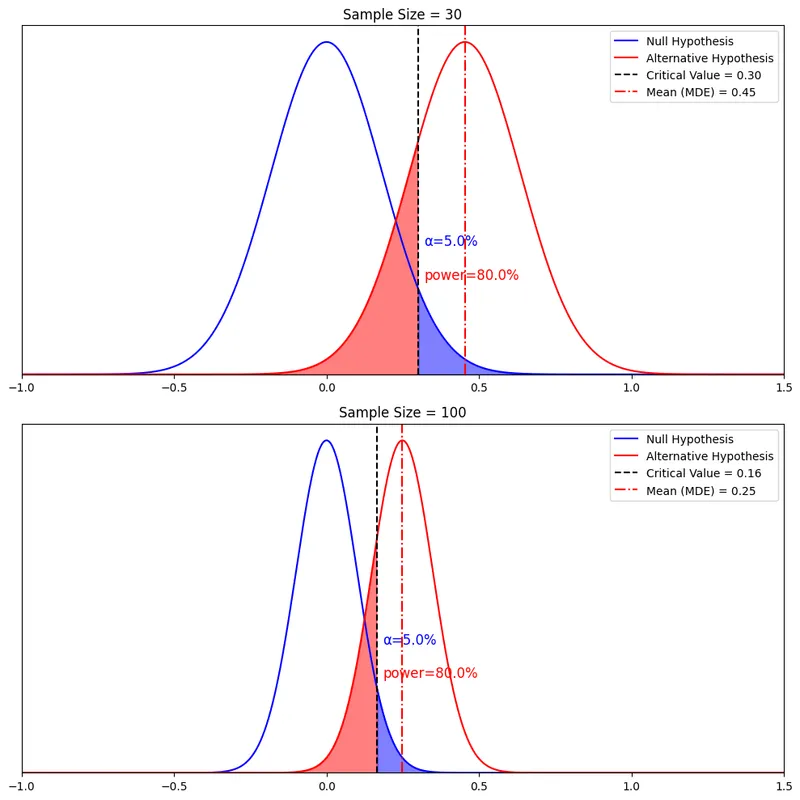
Statistical power definition US Medical PG Question 7: You are reading through a recent article that reports significant decreases in all-cause mortality for patients with malignant melanoma following treatment with a novel biological infusion. Which of the following choices refers to the probability that a study will find a statistically significant difference when one truly does exist?
- A. Type II error
- B. Type I error
- C. Confidence interval
- D. p-value
- E. Power (Correct Answer)
Statistical power definition Explanation: ***Power***
- **Power** is the probability that a study will correctly reject the null hypothesis when it is, in fact, false (i.e., will find a statistically significant difference when one truly exists).
- A study with high power minimizes the risk of a **Type II error** (failing to detect a real effect).
*Type II error*
- A **Type II error** (or **beta error**) occurs when a study fails to reject a false null hypothesis, meaning it concludes there is no significant difference when one actually exists.
- This is the **opposite** of what the question describes, which asks for the probability of *finding* a difference.
*Type I error*
- A **Type I error** (or **alpha error**) occurs when a study incorrectly rejects a true null hypothesis, concluding there is a significant difference when one does not actually exist.
- This relates to the **p-value** and the level of statistical significance (e.g., p < 0.05).
*Confidence interval*
- A **confidence interval** provides a range of values within which the true population parameter is likely to lie with a certain degree of confidence (e.g., 95%).
- It does not directly represent the probability of finding a statistically significant difference when one truly exists.
*p-value*
- The **p-value** is the probability of observing data as extreme as, or more extreme than, that obtained in the study, assuming the null hypothesis is true.
- It is used to determine statistical significance, but it is not the probability of detecting a true effect.
Statistical power definition US Medical PG Question 8: A health system implements a new sepsis protocol across 20 hospitals. A researcher plans to evaluate effectiveness using a stepped-wedge cluster randomized design where hospitals sequentially adopt the protocol every 3 months. She calculates sample size based on individual patient outcomes (mortality) needing 2,000 patients total. The biostatistician identifies a critical error. Evaluate what modification is needed.
- A. Adjust for multiple time periods using Bonferroni correction
- B. Use hospital-level outcomes instead of patient-level outcomes as unit of analysis
- C. Increase alpha to 0.10 to account for cluster randomization reducing power
- D. Include random effects for both hospital and time period in power calculation
- E. Account for intra-cluster correlation coefficient (ICC) requiring substantial sample size inflation (Correct Answer)
Statistical power definition Explanation: ***Account for intra-cluster correlation coefficient (ICC) requiring substantial sample size inflation***
- In cluster-randomized designs, observations within the same cluster (hospital) are not independent; the **Intra-cluster Correlation Coefficient (ICC)** quantifies this correlation and must be used to calculate a **design effect**.
- Neglecting the ICC leads to an **underpowered study** because the effective sample size is smaller than the total number of individual patients measured.
*Adjust for multiple time periods using Bonferroni correction*
- **Bonferroni correction** is used to control for **Type I error** when performing multiple independent hypothesis tests, not for determining sample size in nested longitudinal designs.
- While the stepped-wedge design involves multiple time points, the primary analysis typically uses a **single model** (e.g., GEE or GLMM) that accounts for time as a fixed effect.
*Use hospital-level outcomes instead of patient-level outcomes as unit of analysis*
- While the hospital is the **unit of randomization**, using hospital-level means as the unit of analysis simplifies the data and causes a significant loss of **statistical information** and precision.
- Modern biostatistical methods utilize **multilevel modeling** to maintain the richness of patient-level data while adjusting for the cluster-level randomization.
*Include random effects for both hospital and time period in power calculation*
- While random effects are important for the **analysis phase**, the "critical error" identified in the prompt refers to the initial failure to inflate the sample size based on **clustering (ICC)**.
- Power calculations for stepped-wedge designs are complex and certainly involve time parameters, but **ICC-based inflation** is the most fundamental adjustment required when moving from individual to cluster randomization.
*Increase alpha to 0.10 to account for cluster randomization reducing power*
- Increasing the **alpha level** (significance threshold) is not a standard or scientifically acceptable method to compensate for the loss of power due to **clustering**.
- Standard practice mandates maintaining an **alpha of 0.05** while appropriately increasing the **sample size** or number of clusters to reach the desired power (usually 80-90%).
Statistical power definition US Medical PG Question 9: A 41-year-old research fellow designs a non-inferiority trial comparing oral to IV antibiotics for osteomyelitis. She sets the non-inferiority margin at 10% (cure rate difference), expects 85% cure in both groups, and calculates 300 patients per arm for 80% power with α=0.025 (one-sided). Her mentor suggests this underestimates required sample size. Evaluate the mentor's concern.
- A. Correct; non-inferiority trials require larger samples than superiority trials for equivalent power (Correct Answer)
- B. Incorrect; non-inferiority trials actually require smaller samples due to less stringent hypotheses
- C. Correct; dropout rates in antibiotic trials necessitate 20% inflation of calculated sample size
- D. Incorrect; the calculation appropriately uses one-sided alpha for non-inferiority testing
- E. Correct; the margin should be set at 5% requiring doubling of sample size
Statistical power definition Explanation: ***Correct; non-inferiority trials require larger samples than superiority trials for equivalent power***
- **Non-inferiority trials** are designed to exclude a difference greater than a pre-specified margin, which typically requires a **larger sample size** than superiority trials investigating the same outcome.
- Because we are proving that the new treatment is "not much worse" (rather than "better"), the **statistical threshold** often necessitates higher enrollment to achieve adequate **power**.
*Incorrect; the calculation appropriately uses one-sided alpha for non-inferiority testing*
- While it is true that **non-inferiority testing** uses a **one-sided alpha (0.025)**, this does not negate the fact that such trials inherently require more participants.
- The mentor's concern is about the **total N**, which remains insufficient despite using the correct one-sided alpha convention.
*Correct; the margin should be set at 5% requiring doubling of sample size*
- There is no universal rule that the **non-inferiority margin** must be 5%; it is determined by **clinical significance** and regulatory standards for the specific condition.
- While a 5% margin would indeed increase the sample size, the 10% margin is often standard in **antibiotic trials** for osteomyelitis.
*Incorrect; non-inferiority trials actually require smaller samples due to less stringent hypotheses*
- This is a common misconception; non-inferiority trials are actually more demanding because the **null hypothesis** assumes the treatments are different (inferior).
- Disproving **inferiority** within a tight **margin (delta)** is statistically more intensive than proving a treatment is superior to a placebo.
*Correct; dropout rates in antibiotic trials necessitate 20% inflation of calculated sample size*
- While **attrition bias** is a concern, there is no fixed rule that every trial needs a **20% inflation** factor.
- The mentor's concern is specifically about the **base calculation** and the statistical nature of non-inferiority designs rather than just the **dropout rate**.
Statistical power definition US Medical PG Question 10: A pharmaceutical company tests a new antidepressant in 500 patients (250 per arm) and finds a 2-point improvement on a 52-point depression scale compared to placebo (p=0.04). The study was originally powered to detect a 4-point difference. The company seeks FDA approval citing statistical significance. Analyze the regulatory and scientific implications.
- A. Approval warranted; the study achieved statistical significance with adequate power
- B. Approval not warranted; observed effect is smaller than pre-specified clinically meaningful difference (Correct Answer)
- C. Approval warranted; post-hoc power analysis shows adequate power for 2-point difference
- D. Approval not warranted; the study was underpowered for the observed effect size
- E. Approval warranted if sensitivity analyses confirm robustness of findings
Statistical power definition Explanation: ***Approval not warranted; observed effect is smaller than pre-specified clinically meaningful difference***
- Although the result is **statistically significant** (p=0.04), the observed 2-point improvement is only half of the **pre-specified 4-point difference** deemed clinically relevant.
- Regulatory bodies like the **FDA** prioritize **clinical significance** over mere p-values, ensuring that a drug provides a meaningful benefit to patients' lives.
*Approval warranted; the study achieved statistical significance with adequate power*
- Statistical significance does not automatically justify approval if the **effect size** is too small to provide a real therapeutic advantage.
- Being **powered** for a 4-point difference means the study was designed to reliably detect a larger effect; a smaller effect may be a result of **over-testing** or limited clinical utility.
*Approval not warranted; the study was underpowered for the observed effect size*
- If a study finds a significant result (p < 0.05), it is by definition **sufficiently powered** to detect that specific effect size in that sample.
- The issue here is not **power** or sample size, but rather the **magnitude of effect** failing to meet the pre-defined target for clinical relevance.
*Approval warranted if sensitivity analyses confirm robustness of findings*
- **Sensitivity analyses** help confirm that results are not driven by outliers, but they cannot transform a **clinically trivial** difference into a meaningful one.
- Even a robust, consistent 2-point difference remains below the **Minimum Clinically Important Difference (MCID)** set at 4 points.
*Approval warranted; post-hoc power analysis shows adequate power for 2-point difference*
- **Post-hoc power analysis** is generally considered scientifically flawed and redundant once the **p-value** is already known.
- Demonstrating power for a 2-point difference does not erase the fact that the drug failed to meet the **threshold of efficacy** defined by the researchers at the start.
More Statistical power definition US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.