Minimally important difference US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Minimally important difference. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Minimally important difference US Medical PG Question 1: A surgeon is interested in studying how different surgical techniques impact the healing of tendon injuries. In particular, he will compare 3 different types of suture repairs biomechanically in order to determine the maximum load before failure of the tendon 2 weeks after repair. He collects data on maximum load for 90 different repaired tendons from an animal model. Thirty tendons were repaired using each of the different suture techniques. Which of the following statistical measures is most appropriate for analyzing the results of this study?
- A. Chi-squared
- B. Wilcoxon rank sum
- C. Pearson r coefficient
- D. Student t-test
- E. ANOVA (Correct Answer)
Minimally important difference Explanation: ***ANOVA***
- **ANOVA (Analysis of Variance)** is appropriate here because it compares the means of **three or more independent groups** (the three different suture techniques) on a continuous dependent variable (maximum load before failure).
- The study has three distinct repair techniques, each with 30 tendons, making ANOVA suitable for determining if there are statistically significant differences among their mean failure loads.
*Chi-squared*
- The **Chi-squared test** is used for analyzing **categorical data** (frequencies or proportions) to determine if there is an association between two nominal variables.
- This study involves quantitative measurement (maximum load), not categorical data, making Chi-squared inappropriate.
*Wilcoxon rank sum*
- The **Wilcoxon rank sum test** (also known as Mann-Whitney U test) is a **non-parametric test** used to compare two independent groups when the data is not normally distributed or is ordinal.
- While the study has independent groups, it involves three groups, and the dependent variable is continuous, making ANOVA a more powerful and appropriate choice assuming normal distribution.
*Pearson r coefficient*
- The **Pearson r coefficient** measures the **strength and direction of a linear relationship between two continuous variables**.
- This study aims to compare means across different groups, not to determine the correlation between two continuous variables.
*Student t-test*
- The **Student t-test** is used to compare the means of **exactly two groups** (either independent or paired) on a continuous dependent variable.
- This study involves comparing three different suture techniques, not just two, making the t-test unsuitable.
Minimally important difference US Medical PG Question 2: A researcher is conducting a study to compare fracture risk in male patients above the age of 65 who received annual DEXA screening to peers who did not receive screening. He conducts a randomized controlled trial in 900 patients, with half of participants assigned to each experimental group. The researcher ultimately finds similar rates of fractures in the two groups. He then notices that he had forgotten to include 400 patients in his analysis. Including the additional participants in his analysis would most likely affect the study's results in which of the following ways?
- A. Wider confidence intervals of results
- B. Increased probability of committing a type II error
- C. Decreased significance level of results
- D. Increased external validity of results
- E. Increased probability of rejecting the null hypothesis when it is truly false (Correct Answer)
Minimally important difference Explanation: ***Increased probability of rejecting the null hypothesis when it is truly false***
- Including more participants increases the **statistical power** of the study, making it more likely to detect a true effect if one exists.
- A higher sample size provides a more precise estimate of the population parameters, leading to a greater ability to **reject a false null hypothesis**.
*Wider confidence intervals of results*
- A larger sample size generally leads to **narrower confidence intervals**, as it reduces the standard error of the estimate.
- Narrower confidence intervals indicate **greater precision** in the estimation of the true population parameter.
*Increased probability of committing a type II error*
- A **Type II error** (false negative) occurs when a study fails to reject a false null hypothesis.
- Increasing the sample size typically **reduces the probability of a Type II error** because it increases statistical power.
*Decreased significance level of results*
- The **significance level (alpha)** is a pre-determined threshold set by the researcher before the study begins, typically 0.05.
- It is independent of sample size and represents the **acceptable probability of committing a Type I error** (false positive).
*Increased external validity of results*
- **External validity** refers to the generalizability of findings to other populations, settings, or times.
- While a larger sample size can enhance the representativeness of the study population, external validity is primarily determined by the **sampling method** and the study's design context, not just sample size alone.
Minimally important difference US Medical PG Question 3: An investigator is measuring the blood calcium level in a sample of female cross country runners and a control group of sedentary females. If she would like to compare the means of the two groups, which statistical test should she use?
- A. Chi-square test
- B. Linear regression
- C. t-test (Correct Answer)
- D. ANOVA (Analysis of Variance)
- E. F-test
Minimally important difference Explanation: ***t-test***
- A **t-test** is appropriate for comparing the means of two independent groups, such as the blood calcium levels between runners and sedentary females.
- It assesses whether the observed difference between the two sample means is statistically significant or occurred by chance.
*Chi-square test*
- The **chi-square test** is used to analyze categorical data to determine if there is a significant association between two variables.
- It is not suitable for comparing continuous variables like blood calcium levels.
*Linear regression*
- **Linear regression** is used to model the relationship between a dependent variable (outcome) and one or more independent variables (predictors).
- It aims to predict the value of a variable based on the value of another, rather than comparing means between groups.
*ANOVA (Analysis of Variance)*
- **ANOVA** is used to compare the means of **three or more independent groups**.
- Since there are only two groups being compared in this scenario, a t-test is more specific and appropriate.
*F-test*
- The **F-test** is primarily used to compare the variances of two populations or to assess the overall significance of a regression model.
- While it is the basis for ANOVA, it is not the direct test for comparing the means of two groups.
Minimally important difference US Medical PG Question 4: A 25-year-old man comes to the physician for severe back pain. He describes the pain as shooting and stabbing. On a 10-point scale, he rates the pain as a 9 to 10. The pain started after he lifted a heavy box at work; he works at a supermarket and recently switched from being a cashier to a storekeeper. The patient appears to be in severe distress. Vital signs are within normal limits. On physical examination, the spine is nontender without paravertebral muscle spasms. Range of motion is normal. A straight-leg raise test is negative. After the physical examination has been completed, the patient asks for a letter to his employer attesting to his inability to work as a storekeeper. Which of the following is the most appropriate response?
- A. “Yes. Since work may worsen your condition, I would prefer that you stay home a few days. I will write a letter to your employer to explain the situation.”
- B. You say you are in severe pain. However, the physical examination findings do not suggest a physical problem that can be addressed with medications or surgery. I'd like to meet on a regular basis to see how you're doing.
- C. I understand that you are uncomfortable, but the findings do not match the severity of your symptoms. Let's talk about the recent changes at your job. (Correct Answer)
- D. The physical exam findings do not match your symptoms, which suggests a psychological problem. I would be happy to refer you to a mental health professional.
- E. The physical exam findings suggest a psychological rather than a physical problem. But there is a good chance that we can address it with cognitive-behavioral therapy.
Minimally important difference Explanation: ***"I understand that you are uncomfortable, but the findings do not match the severity of your symptoms. Let's talk about the recent changes at your job."***
- This response acknowledges the patient's reported discomfort while gently highlighting the **discrepancy between symptoms and objective findings**, which is crucial in cases of suspected **somatoform or functional pain**.
- It also opens communication about potential **psychosocial stressors** related to his job change, which could be contributing to his symptoms, without dismissing his pain or making a premature diagnosis.
*"You say you are in severe pain. However, the physical examination findings do not suggest a physical problem that can be addressed with medications or surgery. I'd like to meet on a regular basis to see how you're doing."*
- While this option correctly identifies the lack of physical findings, it can be perceived as dismissive of the patient's pain, potentially damaging the **physician-patient relationship**.
- Suggesting regular meetings without a clear plan for addressing his immediate concerns or exploring underlying issues might not be the most effective initial approach.
*“Yes. Since work may worsen your condition, I would prefer that you stay home a few days. I will write a letter to your employer to explain the situation.”*
- This response would **validate the patient's claim of severe pain** without objective evidence, potentially reinforcing illness behavior and avoiding addressing the underlying issue.
- Providing a doctor's note for inability to work without a clear diagnostic basis or understanding of the pain's origin is **medically inappropriate** and could set a precedent for future such requests.
*"The physical exam findings do not match your symptoms, which suggests a psychological problem. I would be happy to refer you to a mental health professional."*
- Directly labeling the problem as "psychological" can be **stigmatizing and alienating** to the patient, leading to distrust and resistance to care.
- While a psychological component might be present, immediately referring to mental health without further exploration of the patient's situation or current stressors is premature and lacks empathy.
*"The physical exam findings suggest a psychological rather than a physical problem. But there is a good chance that we can address it with cognitive-behavioral therapy."*
- Similar to the previous option, explicitly stating a "psychological problem" can be **stigmatizing**.
- Jumping directly to recommending **cognitive-behavioral therapy (CBT)** without a comprehensive discussion and patient buy-in is premature and may lead to non-compliance.
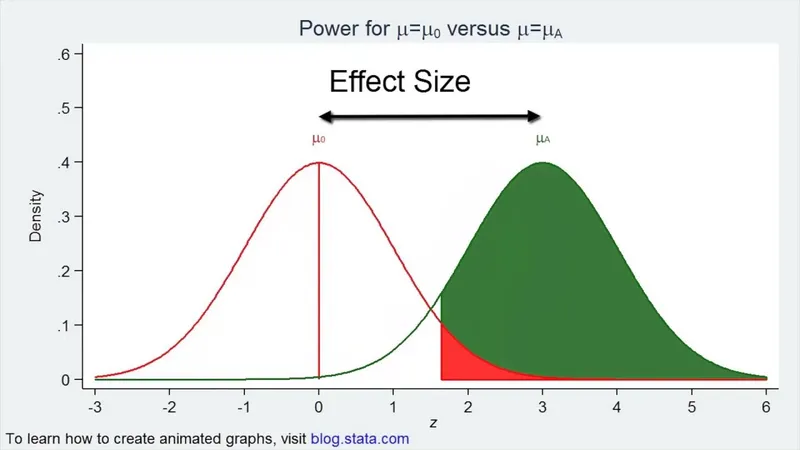
Minimally important difference US Medical PG Question 5: You submit a paper to a prestigious journal about the effects of coffee consumption on mesothelioma risk. The first reviewer lauds your clinical and scientific acumen, but expresses concern that your study does not have adequate statistical power. Statistical power refers to which of the following?
- A. The probability of detecting an association when no association exists.
- B. The probability of not detecting an association when an association does exist.
- C. The probability of detecting an association when an association does exist. (Correct Answer)
- D. The first derivative of work.
- E. The square root of the variance.
Minimally important difference Explanation: ***The probability of detecting an association when an association does exist.***
- **Statistical power** is defined as the probability that a study will correctly reject a false null hypothesis, meaning it will detect a true effect or association if one exists.
- A study with **adequate statistical power** is less likely to miss a real effect.
*The probability of detecting an association when no association exists.*
- This describes a **Type I error** or **false positive**, often represented by **alpha (α)**.
- It is the probability of incorrectly concluding an effect or association exists when, in reality, there is none.
*The probability of not detecting an association when an association does exist.*
- This refers to a **Type II error** or **false negative**, represented by **beta (β)**.
- **Statistical power** is calculated as **1 - β**, so this option describes the complement of power.
*The first derivative of work.*
- The first derivative of work with respect to time represents **power** in physics, which is the rate at which work is done.
- This option is a **distractor** from physics and is unrelated to statistical power in research.
*The square root of the variance.*
- The **square root of the variance** is the **standard deviation**, a measure of the dispersion or spread of data.
- This is a statistical concept but is not the definition of statistical power.
Minimally important difference US Medical PG Question 6: You are currently employed as a clinical researcher working on clinical trials of a new drug to be used for the treatment of Parkinson's disease. Currently, you have already determined the safe clinical dose of the drug in a healthy patient. You are in the phase of drug development where the drug is studied in patients with the target disease to determine its efficacy. Which of the following phases is this new drug currently in?
- A. Phase 4
- B. Phase 1
- C. Phase 2 (Correct Answer)
- D. Phase 0
- E. Phase 3
Minimally important difference Explanation: ***Phase 2***
- **Phase 2 trials** involve studying the drug in patients with the target disease to assess its **efficacy** and further evaluate safety, typically involving a few hundred patients.
- The question describes a stage after safe dosing in healthy patients (Phase 1) and before large-scale efficacy confirmation (Phase 3), focusing on efficacy in the target population.
*Phase 4*
- **Phase 4 trials** occur **after a drug has been approved** and marketed, monitoring long-term effects, optimal use, and rare side effects in a diverse patient population.
- This phase is conducted post-market approval, whereas the question describes a drug still in development prior to approval.
*Phase 1*
- **Phase 1 trials** primarily focus on determining the **safety and dosage** of a new drug in a **small group of healthy volunteers** (or sometimes patients with advanced disease if the drug is highly toxic).
- The question states that the safe clinical dose in a healthy patient has already been determined, indicating that Phase 1 has been completed.
*Phase 0*
- **Phase 0 trials** are exploratory, very early-stage studies designed to confirm that the drug reaches the target and acts as intended, typically involving a very small number of doses and participants.
- These trials are conducted much earlier in the development process, preceding the determination of safe clinical doses and large-scale efficacy studies.
*Phase 3*
- **Phase 3 trials** are large-scale studies involving hundreds to thousands of patients to confirm **efficacy**, monitor side effects, compare it to commonly used treatments, and collect information that will allow the drug to be used safely.
- While Phase 3 does assess efficacy, it follows Phase 2 and is typically conducted on a much larger scale before submitting for regulatory approval.
Minimally important difference US Medical PG Question 7: In a randomized controlled trial studying a new treatment, the primary endpoint (mortality) occurred in 14.4% of the treatment group and 16.7% of the control group. Which of the following represents the number of patients needed to treat to save one life, based on the primary endpoint?
- A. 1/(0.144 - 0.167)
- B. 1/(0.167 - 0.144) (Correct Answer)
- C. 1/(0.300 - 0.267)
- D. 1/(0.267 - 0.300)
- E. 1/(0.136 - 0.118)
Minimally important difference Explanation: ***1/(0.167 - 0.144)***
- The **Number Needed to Treat (NNT)** is calculated as **1 / Absolute Risk Reduction (ARR)**.
- The **Absolute Risk Reduction (ARR)** is the difference between the event rate in the control group (16.7%) and the event rate in the treatment group (14.4%), which is **0.167 - 0.144**.
*1/(0.144 - 0.167)*
- This calculation represents 1 divided by the **Absolute Risk Increase**, which would be relevant if the treatment increased mortality.
- The **NNT should always be a positive value**, indicating the number of patients to treat to prevent one adverse event.
*1/(0.300 - 0.267)*
- This option uses arbitrary numbers (0.300 and 0.267) that do not correspond to the given **mortality rates** in the problem.
- It does not reflect the correct calculation for **absolute risk reduction** based on the provided data.
*1/(0.267 - 0.300)*
- This option also uses arbitrary numbers not derived from the problem's data, and it would result in a **negative value** for the denominator.
- The difference between event rates of 0.267 and 0.300 is not present in the given information for this study.
*1/(0.136 - 0.118)*
- This calculation uses arbitrary numbers (0.136 and 0.118) that are not consistent with the reported **mortality rates** of 14.4% and 16.7%.
- These values do not represent the **Absolute Risk Reduction** required for calculating NNT in this specific scenario.
Minimally important difference US Medical PG Question 8: A 28-year-old male presents to his primary care physician with complaints of intermittent abdominal pain and alternating bouts of constipation and diarrhea. His medical chart is not significant for any past medical problems or prior surgeries. He is not prescribed any current medications. Which of the following questions would be the most useful next question in eliciting further history from this patient?
- A. "Does the diarrhea typically precede the constipation, or vice-versa?"
- B. "Is the diarrhea foul-smelling?"
- C. "Please rate your abdominal pain on a scale of 1-10, with 10 being the worst pain of your life"
- D. "Are the symptoms worse in the morning or at night?"
- E. "Can you tell me more about the symptoms you have been experiencing?" (Correct Answer)
Minimally important difference Explanation: ***Can you tell me more about the symptoms you have been experiencing?***
- This **open-ended question** encourages the patient to provide a **comprehensive narrative** of their symptoms, including details about onset, frequency, duration, alleviating/aggravating factors, and associated symptoms, which is crucial for diagnosis.
- In a patient presenting with vague, intermittent symptoms like alternating constipation and diarrhea, allowing them to elaborate freely can reveal important clues that might not be captured by more targeted questions.
*Does the diarrhea typically precede the constipation, or vice-versa?*
- While knowing the sequence of symptoms can be helpful in understanding the **pattern of bowel dysfunction**, it is a very specific question that might overlook other important aspects of the patient's experience.
- It prematurely narrows the focus without first obtaining a broad understanding of the patient's overall symptomatic picture.
*Is the diarrhea foul-smelling?*
- Foul-smelling diarrhea can indicate **malabsorption** or **bacterial overgrowth**, which are important to consider in some gastrointestinal conditions.
- However, this is a **specific symptom inquiry** that should follow a more general exploration of the patient's symptoms, as it may not be relevant if other crucial details are missed.
*Please rate your abdominal pain on a scale of 1-10, with 10 being the worst pain of your life*
- Quantifying pain intensity is useful for assessing the **severity of discomfort** and monitoring changes over time.
- However, for a patient with intermittent rather than acute, severe pain, understanding the **character, location, and triggers** of the pain is often more diagnostically valuable than just a numerical rating initially.
*Are the symptoms worse in the morning or at night?*
- Diurnal variation can be relevant in certain conditions, such as inflammatory bowel diseases where nocturnal symptoms might be more concerning, or functional disorders whose symptoms might be stress-related.
- This is another **specific question** that should come after gathering a more complete initial picture of the patient's symptoms to ensure no key information is overlooked.
Minimally important difference US Medical PG Question 9: A health system implements a new sepsis protocol across 20 hospitals. A researcher plans to evaluate effectiveness using a stepped-wedge cluster randomized design where hospitals sequentially adopt the protocol every 3 months. She calculates sample size based on individual patient outcomes (mortality) needing 2,000 patients total. The biostatistician identifies a critical error. Evaluate what modification is needed.
- A. Adjust for multiple time periods using Bonferroni correction
- B. Use hospital-level outcomes instead of patient-level outcomes as unit of analysis
- C. Increase alpha to 0.10 to account for cluster randomization reducing power
- D. Include random effects for both hospital and time period in power calculation
- E. Account for intra-cluster correlation coefficient (ICC) requiring substantial sample size inflation (Correct Answer)
Minimally important difference Explanation: ***Account for intra-cluster correlation coefficient (ICC) requiring substantial sample size inflation***
- In cluster-randomized designs, observations within the same cluster (hospital) are not independent; the **Intra-cluster Correlation Coefficient (ICC)** quantifies this correlation and must be used to calculate a **design effect**.
- Neglecting the ICC leads to an **underpowered study** because the effective sample size is smaller than the total number of individual patients measured.
*Adjust for multiple time periods using Bonferroni correction*
- **Bonferroni correction** is used to control for **Type I error** when performing multiple independent hypothesis tests, not for determining sample size in nested longitudinal designs.
- While the stepped-wedge design involves multiple time points, the primary analysis typically uses a **single model** (e.g., GEE or GLMM) that accounts for time as a fixed effect.
*Use hospital-level outcomes instead of patient-level outcomes as unit of analysis*
- While the hospital is the **unit of randomization**, using hospital-level means as the unit of analysis simplifies the data and causes a significant loss of **statistical information** and precision.
- Modern biostatistical methods utilize **multilevel modeling** to maintain the richness of patient-level data while adjusting for the cluster-level randomization.
*Include random effects for both hospital and time period in power calculation*
- While random effects are important for the **analysis phase**, the "critical error" identified in the prompt refers to the initial failure to inflate the sample size based on **clustering (ICC)**.
- Power calculations for stepped-wedge designs are complex and certainly involve time parameters, but **ICC-based inflation** is the most fundamental adjustment required when moving from individual to cluster randomization.
*Increase alpha to 0.10 to account for cluster randomization reducing power*
- Increasing the **alpha level** (significance threshold) is not a standard or scientifically acceptable method to compensate for the loss of power due to **clustering**.
- Standard practice mandates maintaining an **alpha of 0.05** while appropriately increasing the **sample size** or number of clusters to reach the desired power (usually 80-90%).
Minimally important difference US Medical PG Question 10: A 41-year-old research fellow designs a non-inferiority trial comparing oral to IV antibiotics for osteomyelitis. She sets the non-inferiority margin at 10% (cure rate difference), expects 85% cure in both groups, and calculates 300 patients per arm for 80% power with α=0.025 (one-sided). Her mentor suggests this underestimates required sample size. Evaluate the mentor's concern.
- A. Correct; non-inferiority trials require larger samples than superiority trials for equivalent power (Correct Answer)
- B. Incorrect; non-inferiority trials actually require smaller samples due to less stringent hypotheses
- C. Correct; dropout rates in antibiotic trials necessitate 20% inflation of calculated sample size
- D. Incorrect; the calculation appropriately uses one-sided alpha for non-inferiority testing
- E. Correct; the margin should be set at 5% requiring doubling of sample size
Minimally important difference Explanation: ***Correct; non-inferiority trials require larger samples than superiority trials for equivalent power***
- **Non-inferiority trials** are designed to exclude a difference greater than a pre-specified margin, which typically requires a **larger sample size** than superiority trials investigating the same outcome.
- Because we are proving that the new treatment is "not much worse" (rather than "better"), the **statistical threshold** often necessitates higher enrollment to achieve adequate **power**.
*Incorrect; the calculation appropriately uses one-sided alpha for non-inferiority testing*
- While it is true that **non-inferiority testing** uses a **one-sided alpha (0.025)**, this does not negate the fact that such trials inherently require more participants.
- The mentor's concern is about the **total N**, which remains insufficient despite using the correct one-sided alpha convention.
*Correct; the margin should be set at 5% requiring doubling of sample size*
- There is no universal rule that the **non-inferiority margin** must be 5%; it is determined by **clinical significance** and regulatory standards for the specific condition.
- While a 5% margin would indeed increase the sample size, the 10% margin is often standard in **antibiotic trials** for osteomyelitis.
*Incorrect; non-inferiority trials actually require smaller samples due to less stringent hypotheses*
- This is a common misconception; non-inferiority trials are actually more demanding because the **null hypothesis** assumes the treatments are different (inferior).
- Disproving **inferiority** within a tight **margin (delta)** is statistically more intensive than proving a treatment is superior to a placebo.
*Correct; dropout rates in antibiotic trials necessitate 20% inflation of calculated sample size*
- While **attrition bias** is a concern, there is no fixed rule that every trial needs a **20% inflation** factor.
- The mentor's concern is specifically about the **base calculation** and the statistical nature of non-inferiority designs rather than just the **dropout rate**.
More Minimally important difference US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.