Effect size estimation US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Effect size estimation. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Effect size estimation US Medical PG Question 1: A 25-year-old man with a genetic disorder presents for genetic counseling because he is concerned about the risk that any children he has will have the same disease as himself. Specifically, since childhood he has had difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy. He has also had diarrhea and malabsorption requiring enzyme replacement therapy. If his wife comes from a population where 1 in 10,000 people are affected by this same disorder, which of the following best represents the likelihood a child would be affected as well?
- A. 0.01%
- B. 2%
- C. 0.5%
- D. 1% (Correct Answer)
- E. 50%
Effect size estimation Explanation: ***Correct Option: 1%***
- The patient's symptoms (difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy; diarrhea and malabsorption requiring enzyme replacement therapy) are classic for **cystic fibrosis (CF)**, an **autosomal recessive disorder**.
- For an autosomal recessive disorder with a prevalence of 1 in 10,000 in the general population, **q² = 1/10,000**, so **q = 1/100 = 0.01**. The carrier frequency **(2pq)** is approximately **2q = 2 × (1/100) = 1/50 = 0.02**.
- The affected man is **homozygous recessive (aa)** and will always pass on the recessive allele. His wife has a **1/50 chance of being a carrier (Aa)**. If she is a carrier, she has a **1/2 chance of passing on the recessive allele**.
- Therefore, the probability of an affected child = **(Probability wife is a carrier) × (Probability wife passes recessive allele) = 1/50 × 1/2 = 1/100 = 1%**.
*Incorrect Option: 0.01%*
- This percentage is too low and does not correctly account for the carrier frequency in the population and the probability of transmission from a carrier mother.
*Incorrect Option: 2%*
- This represents approximately the carrier frequency (1/50 ≈ 2%), but does not account for the additional 1/2 probability that a carrier mother would pass on the recessive allele.
*Incorrect Option: 0.5%*
- This value would be correct if the carrier frequency were 1/100 instead of 1/50, which does not match the given population prevalence.
*Incorrect Option: 50%*
- **50%** would be the risk if both parents were carriers of an autosomal recessive disorder (1/4 chance = 25% for affected, but if we know one parent passes the allele, conditional probability changes). More accurately, 50% would apply if the disorder were **autosomal dominant** with one affected parent, which is not the case here.
Effect size estimation US Medical PG Question 2: A randomized control double-blind study is conducted on the efficacy of 2 sulfonylureas. The study concluded that medication 1 was more efficacious in lowering fasting blood glucose than medication 2 (p ≤ 0.05; 95% CI: 14 [10-21]). Which of the following is true regarding a 95% confidence interval (CI)?
- A. If the same study were repeated multiple times, approximately 95% of the calculated confidence intervals would contain the true population parameter. (Correct Answer)
- B. The 95% confidence interval is the probability chosen by the researcher to be the threshold of statistical significance.
- C. When a 95% CI for the estimated difference between groups contains the value ‘0’, the results are significant.
- D. It represents the probability that chance would not produce the difference shown, 95% of the time.
- E. The study is adequately powered at the 95% confidence interval.
Effect size estimation Explanation: ***If the same study were repeated multiple times, approximately 95% of the calculated confidence intervals would contain the true population parameter.***
- This statement accurately defines the **frequentist interpretation** of a confidence interval (CI). It reflects the long-run behavior of the CI over hypothetical repetitions of the study.
- A 95% CI means that if you were to repeat the experiment many times, 95% of the CIs calculated from those experiments would capture the **true underlying population parameter**.
*The 95% confidence interval is the probability chosen by the researcher to be the threshold of statistical significance.*
- The **alpha level (α)**, typically set at 0.05 (or 5%), is the threshold for statistical significance (p ≤ 0.05), representing the probability of a Type I error.
- The 95% confidence level (1-α) is related to statistical significance, but it is not the *threshold* itself; rather, it indicates the **reliability** of the interval estimate.
*When a 95% CI for the estimated difference between groups contains the value ‘0’, the results are significant.*
- If a 95% CI for the difference between groups **contains 0**, it implies that there is **no statistically significant difference** between the groups at the 0.05 alpha level.
- A statistically significant difference (p ≤ 0.05) would be indicated if the 95% CI **does NOT contain 0**, suggesting that the intervention had a real effect.
*It represents the probability that chance would not produce the difference shown, 95% of the time.*
- This statement misinterprets the meaning of a CI and probability. The chance of not producing the observed difference is typically addressed by the **p-value**, not directly by the CI in this manner.
- A CI provides a **range of plausible values** for the population parameter, not a probability about the role of chance in producing the observed difference.
*The study is adequately powered at the 95% confidence interval.*
- **Statistical power** is the probability of correctly rejecting a false null hypothesis, typically set at 80% or 90%. It is primarily determined by sample size, effect size, and alpha level.
- A 95% CI is a measure of the **precision** of an estimate, while power refers to the **ability of a study to detect an effect** if one exists. They are related but distinct concepts.
Effect size estimation US Medical PG Question 3: A surgeon is interested in studying how different surgical techniques impact the healing of tendon injuries. In particular, he will compare 3 different types of suture repairs biomechanically in order to determine the maximum load before failure of the tendon 2 weeks after repair. He collects data on maximum load for 90 different repaired tendons from an animal model. Thirty tendons were repaired using each of the different suture techniques. Which of the following statistical measures is most appropriate for analyzing the results of this study?
- A. Chi-squared
- B. Wilcoxon rank sum
- C. Pearson r coefficient
- D. Student t-test
- E. ANOVA (Correct Answer)
Effect size estimation Explanation: ***ANOVA***
- **ANOVA (Analysis of Variance)** is appropriate here because it compares the means of **three or more independent groups** (the three different suture techniques) on a continuous dependent variable (maximum load before failure).
- The study has three distinct repair techniques, each with 30 tendons, making ANOVA suitable for determining if there are statistically significant differences among their mean failure loads.
*Chi-squared*
- The **Chi-squared test** is used for analyzing **categorical data** (frequencies or proportions) to determine if there is an association between two nominal variables.
- This study involves quantitative measurement (maximum load), not categorical data, making Chi-squared inappropriate.
*Wilcoxon rank sum*
- The **Wilcoxon rank sum test** (also known as Mann-Whitney U test) is a **non-parametric test** used to compare two independent groups when the data is not normally distributed or is ordinal.
- While the study has independent groups, it involves three groups, and the dependent variable is continuous, making ANOVA a more powerful and appropriate choice assuming normal distribution.
*Pearson r coefficient*
- The **Pearson r coefficient** measures the **strength and direction of a linear relationship between two continuous variables**.
- This study aims to compare means across different groups, not to determine the correlation between two continuous variables.
*Student t-test*
- The **Student t-test** is used to compare the means of **exactly two groups** (either independent or paired) on a continuous dependent variable.
- This study involves comparing three different suture techniques, not just two, making the t-test unsuitable.
Effect size estimation US Medical PG Question 4: A study is being conducted on depression using the Patient Health questionnaire (PHQ-9) survey data embedded within a popular social media network with a response size of 500,000 participants. The sample population of this study is approximately normal. The mean PHQ-9 score is 14, and the standard deviation is 4. How many participants have scores greater than 22?
- A. 175,000
- B. 17,500
- C. 160,000
- D. 12,500 (Correct Answer)
- E. 25,000
Effect size estimation Explanation: ***12,500***
- To find the number of participants with scores greater than 22, first calculate the **z-score** for a score of 22: $Z = \frac{(X - \mu)}{\sigma} = \frac{(22 - 14)}{4} = 2$.
- A z-score of 2 means the score is **2 standard deviations above the mean**. Using the **empirical rule** for a normal distribution, approximately **2.5%** of the data falls beyond 2 standard deviations above the mean (5% total in both tails, so 2.5% in each tail).
- Therefore, $2.5\%$ of the total 500,000 participants is $0.025 \times 500,000 = 12,500$.
*175,000*
- This option would imply a much larger proportion of the population scoring above 22, inconsistent with the **normal distribution's properties** and the calculated z-score.
- It would correspond to a z-score closer to 0, indicating a score closer to the mean, not two standard deviations above it.
*17,500*
- This value represents **3.5%** of the total population ($17,500 / 500,000 = 0.035$).
- A proportion of 3.5% above the mean corresponds to a z-score that is not exactly 2, indicating an incorrect calculation or interpretation of the **normal distribution table**.
*160,000*
- This option represents a very large portion of the participants, roughly **32%** of the total population.
- This percentage would correspond to scores within one standard deviation of the mean, not scores 2 standard deviations above the mean as calculated.
*25,000*
- This value represents **5%** of the total population ($25,000 / 500,000 = 0.05$).
- A z-score greater than 2 corresponds to the far tail of the normal distribution, where only 2.5% of the data lies, not 5%. This would correspond to a z-score of approximately 1.65.
Effect size estimation US Medical PG Question 5: You are currently employed as a clinical researcher working on clinical trials of a new drug to be used for the treatment of Parkinson's disease. Currently, you have already determined the safe clinical dose of the drug in a healthy patient. You are in the phase of drug development where the drug is studied in patients with the target disease to determine its efficacy. Which of the following phases is this new drug currently in?
- A. Phase 4
- B. Phase 1
- C. Phase 2 (Correct Answer)
- D. Phase 0
- E. Phase 3
Effect size estimation Explanation: ***Phase 2***
- **Phase 2 trials** involve studying the drug in patients with the target disease to assess its **efficacy** and further evaluate safety, typically involving a few hundred patients.
- The question describes a stage after safe dosing in healthy patients (Phase 1) and before large-scale efficacy confirmation (Phase 3), focusing on efficacy in the target population.
*Phase 4*
- **Phase 4 trials** occur **after a drug has been approved** and marketed, monitoring long-term effects, optimal use, and rare side effects in a diverse patient population.
- This phase is conducted post-market approval, whereas the question describes a drug still in development prior to approval.
*Phase 1*
- **Phase 1 trials** primarily focus on determining the **safety and dosage** of a new drug in a **small group of healthy volunteers** (or sometimes patients with advanced disease if the drug is highly toxic).
- The question states that the safe clinical dose in a healthy patient has already been determined, indicating that Phase 1 has been completed.
*Phase 0*
- **Phase 0 trials** are exploratory, very early-stage studies designed to confirm that the drug reaches the target and acts as intended, typically involving a very small number of doses and participants.
- These trials are conducted much earlier in the development process, preceding the determination of safe clinical doses and large-scale efficacy studies.
*Phase 3*
- **Phase 3 trials** are large-scale studies involving hundreds to thousands of patients to confirm **efficacy**, monitor side effects, compare it to commonly used treatments, and collect information that will allow the drug to be used safely.
- While Phase 3 does assess efficacy, it follows Phase 2 and is typically conducted on a much larger scale before submitting for regulatory approval.
Effect size estimation US Medical PG Question 6: A 52-year-old man presents to the office for a regular health checkup. He was diagnosed with type 2 diabetes mellitus 6 years ago and has been taking metformin alone. Over the past year, his daily blood glucose measurements have gradually been increasing. During his previous visit, his HbA1c level was 7.9% and the doctor mentioned the possibility of requiring an additional medication to keep his blood sugar under better control. Today, his HbA1c is 9%. The doctor mentions a research article that has been conducted on a randomized and controlled group of 200 subjects studying a new anti-diabetic medication. It has been shown to significantly reduce glucose levels and HbA1c levels compared to the current gold standard treatment. Possible adverse effects, however, are still being studied, though the authors believe that they will be minimal. In this study, what would most likely increase the chances of detecting a significant adverse effect?
- A. Decreasing post-market surveillance time
- B. Non-randomization
- C. Decreasing sample size
- D. Increasing selection bias
- E. Increasing sample size (Correct Answer)
Effect size estimation Explanation: ***Increasing sample size***
- A **larger sample size** increases the **statistical power** of a study, making it more likely to detect a real difference or effect, including rare adverse events.
- With more participants, there's a higher chance of observing adverse effects that might only occur in a small percentage of individuals.
*Decreasing post-market surveillance time*
- **Post-market surveillance** occurs *after* a drug is approved and involves monitoring thousands, or even millions, of patients for adverse events.
- **Decreasing** this time would *reduce* the likelihood of detecting rare or long-term adverse effects, as the exposure period and number of observed patients would be smaller.
*Non-randomization*
- **Non-randomization** can introduce **confounding variables** and **bias**, making it difficult to attribute observed effects solely to the medication.
- While it might reveal an association, it doesn't necessarily strengthen the ability to precisely identify significant adverse effects versus other contributing factors.
*Decreasing sample size*
- A **smaller sample size** reduces the **statistical power** of a study, making it less likely to detect a true difference or effect, especially for uncommon adverse events.
- Rare adverse effects are less likely to be observed in a small group of participants.
*Increasing selection bias*
- **Selection bias** occurs when the study participants are not representative of the general population or when groups are not comparable, leading to skewed results.
- This bias can *obscure* or *misrepresent* the true incidence of adverse effects, making accurate detection more difficult, rather than increasing it.
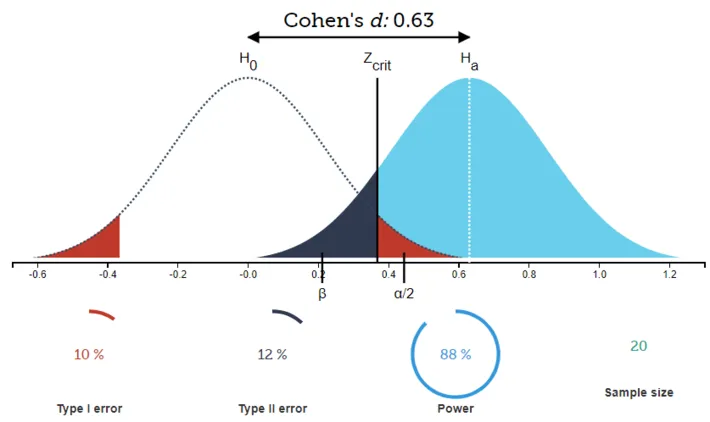
Effect size estimation US Medical PG Question 7: The height of American adults is expected to follow a normal distribution, with a typical male adult having an average height of 69 inches with a standard deviation of 0.1 inches. An investigator has been informed about a community in the American Midwest with a history of heavy air and water pollution in which a lower mean height has been reported. The investigator plans to sample 30 male residents to test the claim that heights in this town differ significantly from the national average based on heights assumed be normally distributed. The significance level is set at 10% and the probability of a type 2 error is assumed to be 15%. Based on this information, which of the following is the power of the proposed study?
- A. 0.10
- B. 0.85 (Correct Answer)
- C. 0.90
- D. 0.15
- E. 0.05
Effect size estimation Explanation: ***0.85***
- **Power** is defined as **1 - β**, where β is the **probability of a Type II error**.
- Given that the probability of a **Type II error (β)** is 15% or 0.15, the power of the study is 1 - 0.15 = **0.85**.
*0.10*
- This value represents the **significance level (α)**, which is the probability of committing a **Type I error** (rejecting a true null hypothesis).
- The significance level is distinct from the **power of the study**, which relates to Type II errors.
*0.90*
- This value would be the power if the **Type II error rate (β)** was 0.10 (1 - 0.10 = 0.90), but the question specifies a β of 0.15.
- It is also the complement of the significance level (1 - α), which is not the definition of power.
*0.15*
- This value is the **probability of a Type II error (β)**, not the power of the study.
- **Power** is the probability of correctly rejecting a false null hypothesis, which is 1 - β.
*0.05*
- While 0.05 is a common significance level (α), it is not given as the significance level in this question (which is 0.10).
- This value also does not represent the power of the study, which would be calculated using the **Type II error rate**.
Effect size estimation US Medical PG Question 8: In 2013 the national mean score on the USMLE Step 1 exam was 227 with a standard deviation of 22. Assuming that the scores for 15,000 people follow a normal distribution, approximately how many students scored above the mean but below 250?
- A. 5,100 (Correct Answer)
- B. 4,500
- C. 6,000
- D. 3,750
- E. 6,750
Effect size estimation Explanation: ***5,100***
- To solve this, first calculate the **z-score** for 250: (250 - 227) / 22 = 1.045.
- Using a **z-table**, the area under the curve from the mean (z=0) to z=1.045 is approximately 0.353. Multiplying this by 15,000 students gives approximately **5,295 students**, which is closest to 5,100.
*4,500*
- This answer would imply a smaller proportion of students between the mean and 250 (around 30%), which is lower than the calculated z-score of 1.045 suggests.
- It does not accurately reflect the area under the **normal distribution curve** for the given range.
*6,000*
- This option would mean that approximately 40% of students scored in this range, which would correspond to a z-score much higher than 1.045 or a different standard deviation.
- This calculation overestimates the number of students within the specified range.
*3,750*
- This value represents 25% of the total students (15,000 * 0.25), indicating that only a quarter of the distribution lies in this range.
- This significantly underestimates the proportion of students scoring between the mean and 250 for the given standard deviation.
*6,750*
- This option reflects approximately 45% of the total student population (15,000 * 0.45), which would correspond to a much larger z-score or a different distribution.
- This value is an overestimation and does not align with the standard normal distribution probabilities for the given parameters.
Effect size estimation US Medical PG Question 9: The mean, median, and mode weight of 37 newborns in a hospital nursery is 7 lbs 2 oz. In fact, there are 7 infants in the nursery that weigh exactly 7 lbs 2 oz. The standard deviation of the weights is 2 oz. The weights follow a normal distribution. A newborn delivered at 10 lbs 2 oz is added to the data set. What is most likely to happen to the mean, median, and mode with the addition of this new data point?
- A. The mean will increase; the median will increase; the mode will stay the same
- B. The mean will increase; the median will stay the same; the mode will stay the same (Correct Answer)
- C. The mean will stay the same; the median will increase; the mode will stay the same
- D. The mean will increase; the median will increase; the mode will increase
- E. The mean will stay the same; the median will increase; the mode will increase
Effect size estimation Explanation: ***The mean will increase; the median will stay the same; the mode will stay the same***
- The **mean** is highly sensitive to outliers. Adding a newborn weighing 10 lbs 2 oz (significantly heavier than the original mean of 7 lbs 2 oz) will increase the total sum of weights, thus **increasing the mean**.
- The **median** is the middle value in an ordered dataset. With 37 newborns, the median is the 19th value. Adding one more (38 total) makes the median the average of the 19th and 20th values. Since the new value (10 lbs 2 oz) is added at the extreme high end of the distribution, the 19th and 20th positions contain the same values as before. Therefore, the median will **stay the same**.
- The **mode** is the most frequent value. Since there are 7 infants already at 7 lbs 2 oz, adding a single infant at 10 lbs 2 oz will not change the most frequent weight in the dataset. The mode will **stay the same** at 7 lbs 2 oz.
*The mean will increase; the median will increase; the mode will stay the same*
- While the **mean will increase** due to the added outlier, the **median will not change**. With 38 observations, the median becomes the average of the 19th and 20th values, which remain unchanged since the outlier is added at position 38.
- The **mode** correctly stays at 7 lbs 2 oz as the new data point does not become the most frequent value.
*The mean will stay the same; the median will increase; the mode will stay the same*
- The **mean will not stay the same** because an outlier significantly higher than the current mean will always pull the mean higher.
- The **median will also not increase** as the middle values (19th and 20th positions) remain unchanged when adding an extreme outlier.
*The mean will increase; the median will increase; the mode will increase*
- While the **mean will increase**, the **median will not change** because the middle positions are unaffected by adding one extreme outlier.
- The **mode will not change** as the new data point (10 lbs 2 oz) is unique and doesn't become the most frequent value; 7 lbs 2 oz remains most frequent with 7 occurrences.
*The mean will stay the same; the median will increase; the mode will increase*
- This option is incorrect because the **mean will definitely increase** with the addition of a much larger value.
- The **median will not increase** as it depends on the middle positions, not extreme values.
- The **mode will not increase** as adding one 10 lb 2 oz infant won't make that weight the most frequent.
Effect size estimation US Medical PG Question 10: A first-year medical student is conducting a summer project with his medical school's pediatrics department using adolescent IQ data from a database of 1,252 patients. He observes that the mean IQ of the dataset is 100. The standard deviation was calculated to be 10. Assuming that the values are normally distributed, approximately 87% of the measurements will fall in between which of the following limits?
- A. 85–115 (Correct Answer)
- B. 95–105
- C. 65–135
- D. 80–120
- E. 70–130
Effect size estimation Explanation: ***85–115***
- For a **normal distribution**, approximately 87% of data falls within **±1.5 standard deviations** from the mean.
- With a mean of 100 and a standard deviation of 10, the range is 100 ± (1.5 * 10) = 100 ± 15, which gives **85–115**.
*95–105*
- This range represents **±0.5 standard deviations** from the mean (100 ± 5), which covers only about 38% of the data.
- This is a much narrower range and does not encompass 87% of the observations as required.
*65–135*
- This range represents **±3.5 standard deviations** from the mean (100 ± 35), which would cover over 99.9% of the data.
- Thus, this interval is too wide for 87% of the measurements.
*80–120*
- This range represents **±2 standard deviations** from the mean (100 ± 20), which covers approximately 95% of the data.
- While a common interval, it is wider than necessary for 87% of the data.
*70–130*
- This range represents **±3 standard deviations** from the mean (100 ± 30), which covers approximately 99.7% of the data.
- This interval is significantly wider than required to capture 87% of the data.
More Effect size estimation US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.