Confidence interval construction US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Confidence interval construction. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Confidence interval construction US Medical PG Question 1: Group of 100 medical students took an end of the year exam. The mean score on the exam was 70%, with a standard deviation of 25%. The professor states that a student's score must be within the 95% confidence interval of the mean to pass the exam. Which of the following is the minimum score a student can have to pass the exam?
- A. 45%
- B. 63.75%
- C. 67.5%
- D. 20%
- E. 65% (Correct Answer)
Confidence interval construction Explanation: ***65%***
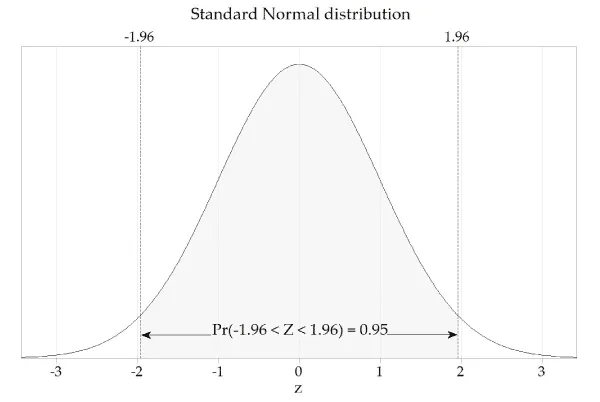
- To find the **95% confidence interval (CI) of the mean**, we use the formula: Mean ± (Z-score × Standard Error). For a 95% CI, the Z-score is approximately **1.96**.
- The **Standard Error (SE)** is calculated as SD/√n, where n is the sample size (100 students). So, SE = 25%/√100 = 25%/10 = **2.5%**.
- The 95% CI is 70% ± (1.96 × 2.5%) = 70% ± 4.9%. The lower bound is 70% - 4.9% = **65.1%**, which rounds to **65%** as the minimum passing score.
*45%*
- This value is significantly lower than the calculated lower bound of the 95% confidence interval (approximately 65.1%).
- It would represent a score far outside the defined passing range.
*63.75%*
- This value falls below the calculated lower bound of the 95% confidence interval (approximately 65.1%).
- While close, this score would not meet the professor's criterion for passing.
*67.5%*
- This value is within the 95% confidence interval (65.1% to 74.9%) but is **not the minimum score**.
- Lower scores within the interval would still qualify as passing.
*20%*
- This score is extremely low and falls significantly outside the 95% confidence interval for a mean of 70%.
- It would indicate performance far below the defined passing threshold.
Confidence interval construction US Medical PG Question 2: A research team develops a new monoclonal antibody checkpoint inhibitor for advanced melanoma that has shown promise in animal studies as well as high efficacy and low toxicity in early phase human clinical trials. The research team would now like to compare this drug to existing standard of care immunotherapy for advanced melanoma. The research team decides to conduct a non-randomized study where the novel drug will be offered to patients who are deemed to be at risk for toxicity with the current standard of care immunotherapy, while patients without such risk factors will receive the standard treatment. Which of the following best describes the level of evidence that this study can offer?
- A. Level 1
- B. Level 3 (Correct Answer)
- C. Level 5
- D. Level 4
- E. Level 2
Confidence interval construction Explanation: ***Level 3***
- A **non-randomized controlled trial** like the one described, where patient assignment to treatment groups is based on specific characteristics (risk of toxicity), falls into Level 3 evidence.
- This level typically includes **non-randomized controlled trials** and **well-designed cohort studies** with comparison groups, which are prone to selection bias and confounding.
- The study compares two treatments but lacks randomization, making it Level 3 evidence.
*Level 1*
- Level 1 evidence is the **highest level of evidence**, derived from **systematic reviews and meta-analyses** of multiple well-designed randomized controlled trials or large, high-quality randomized controlled trials.
- The described study is explicitly stated as non-randomized, ruling out Level 1.
*Level 2*
- Level 2 evidence involves at least one **well-designed randomized controlled trial** (RCT) or **systematic reviews** of randomized trials.
- The current study is *non-randomized*, which means it cannot be classified as Level 2 evidence, as randomization is a key criterion for this level.
*Level 4*
- Level 4 evidence includes **case series**, **case-control studies**, and **poorly designed cohort or case-control studies**.
- While the study is non-randomized, it is a controlled comparative trial rather than a case series or retrospective case-control study, placing it at Level 3.
*Level 5*
- Level 5 evidence is the **lowest level of evidence**, typically consisting of **expert opinion** without explicit critical appraisal, or based on physiology, bench research, or animal studies.
- While the drug was initially tested in animal studies, the current human comparative study offers a higher level of evidence than expert opinion or preclinical data.
Confidence interval construction US Medical PG Question 3: You are conducting a study comparing the efficacy of two different statin medications. Two groups are placed on different statin medications, statin A and statin B. Baseline LDL levels are drawn for each group and are subsequently measured every 3 months for 1 year. Average baseline LDL levels for each group were identical. The group receiving statin A exhibited an 11 mg/dL greater reduction in LDL in comparison to the statin B group. Your statistical analysis reports a p-value of 0.052. Which of the following best describes the meaning of this p-value?
- A. There is a 95% chance that the difference in reduction of LDL observed reflects a real difference between the two groups
- B. Though A is more effective than B, there is a 5% chance the difference in reduction of LDL between the two groups is due to chance
- C. If 100 permutations of this experiment were conducted, 5 of them would show similar results to those described above
- D. This is a statistically significant result
- E. There is a 5.2% chance of observing a difference in reduction of LDL of 11 mg/dL or greater even if the two medications have identical effects (Correct Answer)
Confidence interval construction Explanation: **There is a 5.2% chance of observing a difference in reduction of LDL of 11 mg/dL or greater even if the two medications have identical effects**
- The **p-value** represents the probability of observing results as extreme as, or more extreme than, the observed data, assuming the **null hypothesis** is true (i.e., there is no true difference between the groups).
- A p-value of 0.052 means there's approximately a **5.2% chance** that the observed 11 mg/dL difference (or a more substantial difference) occurred due to **random variation**, even if both statins were equally effective.
*There is a 95% chance that the difference in reduction of LDL observed reflects a real difference between the two groups*
- This statement is an incorrect interpretation of the p-value; it confuses the p-value with the **probability that the alternative hypothesis is true**.
- A p-value does not directly tell us the probability that the observed difference is "real" or due to the intervention being studied.
*Though A is more effective than B, there is a 5% chance the difference in reduction of LDL between the two groups is due to chance*
- This statement implies that Statin A is more effective, which cannot be concluded with a p-value of 0.052 if the significance level (alpha) was set at 0.05.
- While it's true there's a chance the difference is due to chance, claiming A is "more effective" based on this p-value before statistical significance is usually declared is misleading.
*If 100 permutations of this experiment were conducted, 5 of them would show similar results to those described above*
- This is an incorrect interpretation. The p-value does not predict the outcome of repeated experiments in this manner.
- It refers to the **probability under the null hypothesis in a single experiment**, not the frequency of results across multiple hypothetical repetitions.
*This is a statistically significant result*
- A p-value of 0.052 is generally considered **not statistically significant** if the conventional alpha level (significance level) is set at 0.05 (or 5%).
- For a result to be statistically significant at alpha = 0.05, the p-value must be **less than 0.05**.
Confidence interval construction US Medical PG Question 4: A surgeon is interested in studying how different surgical techniques impact the healing of tendon injuries. In particular, he will compare 3 different types of suture repairs biomechanically in order to determine the maximum load before failure of the tendon 2 weeks after repair. He collects data on maximum load for 90 different repaired tendons from an animal model. Thirty tendons were repaired using each of the different suture techniques. Which of the following statistical measures is most appropriate for analyzing the results of this study?
- A. Chi-squared
- B. Wilcoxon rank sum
- C. Pearson r coefficient
- D. Student t-test
- E. ANOVA (Correct Answer)
Confidence interval construction Explanation: ***ANOVA***
- **ANOVA (Analysis of Variance)** is appropriate here because it compares the means of **three or more independent groups** (the three different suture techniques) on a continuous dependent variable (maximum load before failure).
- The study has three distinct repair techniques, each with 30 tendons, making ANOVA suitable for determining if there are statistically significant differences among their mean failure loads.
*Chi-squared*
- The **Chi-squared test** is used for analyzing **categorical data** (frequencies or proportions) to determine if there is an association between two nominal variables.
- This study involves quantitative measurement (maximum load), not categorical data, making Chi-squared inappropriate.
*Wilcoxon rank sum*
- The **Wilcoxon rank sum test** (also known as Mann-Whitney U test) is a **non-parametric test** used to compare two independent groups when the data is not normally distributed or is ordinal.
- While the study has independent groups, it involves three groups, and the dependent variable is continuous, making ANOVA a more powerful and appropriate choice assuming normal distribution.
*Pearson r coefficient*
- The **Pearson r coefficient** measures the **strength and direction of a linear relationship between two continuous variables**.
- This study aims to compare means across different groups, not to determine the correlation between two continuous variables.
*Student t-test*
- The **Student t-test** is used to compare the means of **exactly two groups** (either independent or paired) on a continuous dependent variable.
- This study involves comparing three different suture techniques, not just two, making the t-test unsuitable.
Confidence interval construction US Medical PG Question 5: You are reading through a recent article that reports significant decreases in all-cause mortality for patients with malignant melanoma following treatment with a novel biological infusion. Which of the following choices refers to the probability that a study will find a statistically significant difference when one truly does exist?
- A. Type II error
- B. Type I error
- C. Confidence interval
- D. p-value
- E. Power (Correct Answer)
Confidence interval construction Explanation: ***Power***
- **Power** is the probability that a study will correctly reject the null hypothesis when it is, in fact, false (i.e., will find a statistically significant difference when one truly exists).
- A study with high power minimizes the risk of a **Type II error** (failing to detect a real effect).
*Type II error*
- A **Type II error** (or **beta error**) occurs when a study fails to reject a false null hypothesis, meaning it concludes there is no significant difference when one actually exists.
- This is the **opposite** of what the question describes, which asks for the probability of *finding* a difference.
*Type I error*
- A **Type I error** (or **alpha error**) occurs when a study incorrectly rejects a true null hypothesis, concluding there is a significant difference when one does not actually exist.
- This relates to the **p-value** and the level of statistical significance (e.g., p < 0.05).
*Confidence interval*
- A **confidence interval** provides a range of values within which the true population parameter is likely to lie with a certain degree of confidence (e.g., 95%).
- It does not directly represent the probability of finding a statistically significant difference when one truly exists.
*p-value*
- The **p-value** is the probability of observing data as extreme as, or more extreme than, that obtained in the study, assuming the null hypothesis is true.
- It is used to determine statistical significance, but it is not the probability of detecting a true effect.
Confidence interval construction US Medical PG Question 6: A research group wants to assess the safety and toxicity profile of a new drug. A clinical trial is conducted with 20 volunteers to estimate the maximum tolerated dose and monitor the apparent toxicity of the drug. The study design is best described as which of the following phases of a clinical trial?
- A. Phase 0
- B. Phase III
- C. Phase V
- D. Phase II
- E. Phase I (Correct Answer)
Confidence interval construction Explanation: ***Phase I***
- **Phase I clinical trials** involve a small group of healthy volunteers (typically 20-100) to primarily assess **drug safety**, determine a safe dosage range, and identify side effects.
- The main goal is to establish the **maximum tolerated dose (MTD)** and evaluate the drug's pharmacokinetic and pharmacodynamic profiles.
*Phase 0*
- **Phase 0 trials** are exploratory studies conducted in a very small number of subjects (10-15) to gather preliminary data on a drug's **pharmacodynamics and pharmacokinetics** in humans.
- They involve microdoses, not intended to have therapeutic effects, and thus cannot determine toxicity or MTD.
*Phase III*
- **Phase III trials** are large-scale studies involving hundreds to thousands of patients to confirm the drug's **efficacy**, monitor side effects, compare it to standard treatments, and collect information that will allow the drug to be used safely.
- These trials are conducted after safety and initial efficacy have been established in earlier phases.
*Phase V*
- "Phase V" is not a standard, recognized phase in the traditional clinical trial classification (Phase 0, I, II, III, IV).
- This term might be used in some non-standard research contexts or for post-marketing studies that go beyond Phase IV surveillance, but it is not a formal phase for initial drug development.
*Phase II*
- **Phase II trials** involve several hundred patients with the condition the drug is intended to treat, focusing on **drug efficacy** and further evaluating safety.
- While safety is still monitored, the primary objective shifts to determining if the drug works for its intended purpose and at what dose.
Confidence interval construction US Medical PG Question 7: A pharmaceutical corporation is developing a research study to evaluate a novel blood test to screen for breast cancer. They enrolled 800 patients in the study, half of which have breast cancer. The remaining enrolled patients are age-matched controls who do not have the disease. Of those in the diseased arm, 330 are found positive for the test. Of the patients in the control arm, only 30 are found positive. What is this test’s sensitivity?
- A. 330 / (330 + 30)
- B. 330 / (330 + 70) (Correct Answer)
- C. 370 / (30 + 370)
- D. 370 / (70 + 370)
- E. 330 / (400 + 400)
Confidence interval construction Explanation: ***330 / (330 + 70)***
- **Sensitivity** measures the proportion of actual **positives** that are correctly identified as such.
- In this study, there are **400 diseased patients** (half of 800). Of these, 330 tested positive (true positives), meaning 70 tested negative (false negatives). So sensitivity is **330 / (330 + 70)**.
*330 / (330 + 30)*
- This calculation represents the **positive predictive value**, which is the probability that subjects with a positive screening test truly have the disease. It uses **true positives / (true positives + false positives)**.
- It does not correctly calculate **sensitivity**, which requires knowing the total number of diseased individuals.
*370 / (30 + 370)*
- This expression is attempting to calculate **specificity**, which is the proportion of actual negatives that are correctly identified. It would be **true negatives / (true negatives + false positives)**.
- However, the numbers used are incorrect for specificity in this context given the data provided.
*370 / (70 + 370)*
- This formula is an incorrect combination of values and does not represent any standard epidemiological measure like **sensitivity** or **specificity**.
- It is attempting to combine false negatives (70) and true negatives (370 from control arm) in a non-standard way.
*330 / (400 + 400)*
- This calculation attempts to divide true positives by the total study population (800 patients).
- This metric represents the **prevalence of true positives within the entire study cohort**, not the test's **sensitivity**.
Confidence interval construction US Medical PG Question 8: In a randomized controlled trial studying a new treatment, the primary endpoint (mortality) occurred in 14.4% of the treatment group and 16.7% of the control group. Which of the following represents the number of patients needed to treat to save one life, based on the primary endpoint?
- A. 1/(0.144 - 0.167)
- B. 1/(0.167 - 0.144) (Correct Answer)
- C. 1/(0.300 - 0.267)
- D. 1/(0.267 - 0.300)
- E. 1/(0.136 - 0.118)
Confidence interval construction Explanation: ***1/(0.167 - 0.144)***
- The **Number Needed to Treat (NNT)** is calculated as **1 / Absolute Risk Reduction (ARR)**.
- The **Absolute Risk Reduction (ARR)** is the difference between the event rate in the control group (16.7%) and the event rate in the treatment group (14.4%), which is **0.167 - 0.144**.
*1/(0.144 - 0.167)*
- This calculation represents 1 divided by the **Absolute Risk Increase**, which would be relevant if the treatment increased mortality.
- The **NNT should always be a positive value**, indicating the number of patients to treat to prevent one adverse event.
*1/(0.300 - 0.267)*
- This option uses arbitrary numbers (0.300 and 0.267) that do not correspond to the given **mortality rates** in the problem.
- It does not reflect the correct calculation for **absolute risk reduction** based on the provided data.
*1/(0.267 - 0.300)*
- This option also uses arbitrary numbers not derived from the problem's data, and it would result in a **negative value** for the denominator.
- The difference between event rates of 0.267 and 0.300 is not present in the given information for this study.
*1/(0.136 - 0.118)*
- This calculation uses arbitrary numbers (0.136 and 0.118) that are not consistent with the reported **mortality rates** of 14.4% and 16.7%.
- These values do not represent the **Absolute Risk Reduction** required for calculating NNT in this specific scenario.
Confidence interval construction US Medical PG Question 9: The mean, median, and mode weight of 37 newborns in a hospital nursery is 7 lbs 2 oz. In fact, there are 7 infants in the nursery that weigh exactly 7 lbs 2 oz. The standard deviation of the weights is 2 oz. The weights follow a normal distribution. A newborn delivered at 10 lbs 2 oz is added to the data set. What is most likely to happen to the mean, median, and mode with the addition of this new data point?
- A. The mean will increase; the median will increase; the mode will stay the same
- B. The mean will increase; the median will stay the same; the mode will stay the same (Correct Answer)
- C. The mean will stay the same; the median will increase; the mode will stay the same
- D. The mean will increase; the median will increase; the mode will increase
- E. The mean will stay the same; the median will increase; the mode will increase
Confidence interval construction Explanation: ***The mean will increase; the median will stay the same; the mode will stay the same***
- The **mean** is highly sensitive to outliers. Adding a newborn weighing 10 lbs 2 oz (significantly heavier than the original mean of 7 lbs 2 oz) will increase the total sum of weights, thus **increasing the mean**.
- The **median** is the middle value in an ordered dataset. With 37 newborns, the median is the 19th value. Adding one more (38 total) makes the median the average of the 19th and 20th values. Since the new value (10 lbs 2 oz) is added at the extreme high end of the distribution, the 19th and 20th positions contain the same values as before. Therefore, the median will **stay the same**.
- The **mode** is the most frequent value. Since there are 7 infants already at 7 lbs 2 oz, adding a single infant at 10 lbs 2 oz will not change the most frequent weight in the dataset. The mode will **stay the same** at 7 lbs 2 oz.
*The mean will increase; the median will increase; the mode will stay the same*
- While the **mean will increase** due to the added outlier, the **median will not change**. With 38 observations, the median becomes the average of the 19th and 20th values, which remain unchanged since the outlier is added at position 38.
- The **mode** correctly stays at 7 lbs 2 oz as the new data point does not become the most frequent value.
*The mean will stay the same; the median will increase; the mode will stay the same*
- The **mean will not stay the same** because an outlier significantly higher than the current mean will always pull the mean higher.
- The **median will also not increase** as the middle values (19th and 20th positions) remain unchanged when adding an extreme outlier.
*The mean will increase; the median will increase; the mode will increase*
- While the **mean will increase**, the **median will not change** because the middle positions are unaffected by adding one extreme outlier.
- The **mode will not change** as the new data point (10 lbs 2 oz) is unique and doesn't become the most frequent value; 7 lbs 2 oz remains most frequent with 7 occurrences.
*The mean will stay the same; the median will increase; the mode will increase*
- This option is incorrect because the **mean will definitely increase** with the addition of a much larger value.
- The **median will not increase** as it depends on the middle positions, not extreme values.
- The **mode will not increase** as adding one 10 lb 2 oz infant won't make that weight the most frequent.
Confidence interval construction US Medical PG Question 10: A first-year medical student is conducting a summer project with his medical school's pediatrics department using adolescent IQ data from a database of 1,252 patients. He observes that the mean IQ of the dataset is 100. The standard deviation was calculated to be 10. Assuming that the values are normally distributed, approximately 87% of the measurements will fall in between which of the following limits?
- A. 85–115 (Correct Answer)
- B. 95–105
- C. 65–135
- D. 80–120
- E. 70–130
Confidence interval construction Explanation: ***85–115***
- For a **normal distribution**, approximately 87% of data falls within **±1.5 standard deviations** from the mean.
- With a mean of 100 and a standard deviation of 10, the range is 100 ± (1.5 * 10) = 100 ± 15, which gives **85–115**.
*95–105*
- This range represents **±0.5 standard deviations** from the mean (100 ± 5), which covers only about 38% of the data.
- This is a much narrower range and does not encompass 87% of the observations as required.
*65–135*
- This range represents **±3.5 standard deviations** from the mean (100 ± 35), which would cover over 99.9% of the data.
- Thus, this interval is too wide for 87% of the measurements.
*80–120*
- This range represents **±2 standard deviations** from the mean (100 ± 20), which covers approximately 95% of the data.
- While a common interval, it is wider than necessary for 87% of the data.
*70–130*
- This range represents **±3 standard deviations** from the mean (100 ± 30), which covers approximately 99.7% of the data.
- This interval is significantly wider than required to capture 87% of the data.
More Confidence interval construction US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.