Clinical vs statistical significance US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Clinical vs statistical significance. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Clinical vs statistical significance US Medical PG Question 1: A study is funded by the tobacco industry to examine the association between smoking and lung cancer. They design a study with a prospective cohort of 1,000 smokers between the ages of 20-30. The length of the study is five years. After the study period ends, they conclude that there is no relationship between smoking and lung cancer. Which of the following study features is the most likely reason for the failure of the study to note an association between tobacco use and cancer?
- A. Late-look bias
- B. Latency period (Correct Answer)
- C. Confounding
- D. Effect modification
- E. Pygmalion effect
Clinical vs statistical significance Explanation: ***Latency period***
- **Lung cancer** typically has a **long latency period**, often **20-30+ years**, between initial exposure to tobacco carcinogens and the development of clinically detectable disease.
- A **five-year study duration** in young smokers (ages 20-30) is **far too short** to observe the development of lung cancer, which explains the false negative finding.
- This represents a **fundamental flaw in study design** rather than a bias—the biological timeline of disease development was not adequately considered.
*Late-look bias*
- **Late-look bias** occurs when a study enrolls participants who have already survived the early high-risk period of a disease, leading to **underestimation of true mortality or incidence**.
- Also called **survival bias**, it involves studying a population that has already been "selected" by survival.
- This is not applicable here, as the study simply ended before sufficient time elapsed for disease to develop.
*Confounding*
- **Confounding** occurs when a third variable is associated with both the exposure and outcome, distorting the apparent relationship between them.
- While confounding can affect study results, it would not completely eliminate the detection of a strong, well-established association like smoking and lung cancer in a properly conducted prospective cohort study.
- The issue here is temporal (insufficient follow-up time), not the presence of an unmeasured confounder.
*Effect modification*
- **Effect modification** (also called interaction) occurs when the magnitude of an association between exposure and outcome differs across levels of a third variable.
- This represents a **true biological phenomenon**, not a study design flaw or bias.
- It would not explain the complete failure to detect any association.
*Pygmalion effect*
- The **Pygmalion effect** (observer-expectancy effect) refers to a psychological phenomenon where higher expectations lead to improved performance in the observed subjects.
- This concept is relevant to **behavioral and educational research**, not to objective epidemiological studies of disease incidence.
- It has no relevance to the biological relationship between carcinogen exposure and cancer development.
Clinical vs statistical significance US Medical PG Question 2: You are conducting a study comparing the efficacy of two different statin medications. Two groups are placed on different statin medications, statin A and statin B. Baseline LDL levels are drawn for each group and are subsequently measured every 3 months for 1 year. Average baseline LDL levels for each group were identical. The group receiving statin A exhibited an 11 mg/dL greater reduction in LDL in comparison to the statin B group. Your statistical analysis reports a p-value of 0.052. Which of the following best describes the meaning of this p-value?
- A. There is a 95% chance that the difference in reduction of LDL observed reflects a real difference between the two groups
- B. Though A is more effective than B, there is a 5% chance the difference in reduction of LDL between the two groups is due to chance
- C. If 100 permutations of this experiment were conducted, 5 of them would show similar results to those described above
- D. This is a statistically significant result
- E. There is a 5.2% chance of observing a difference in reduction of LDL of 11 mg/dL or greater even if the two medications have identical effects (Correct Answer)
Clinical vs statistical significance Explanation: **There is a 5.2% chance of observing a difference in reduction of LDL of 11 mg/dL or greater even if the two medications have identical effects**
- The **p-value** represents the probability of observing results as extreme as, or more extreme than, the observed data, assuming the **null hypothesis** is true (i.e., there is no true difference between the groups).
- A p-value of 0.052 means there's approximately a **5.2% chance** that the observed 11 mg/dL difference (or a more substantial difference) occurred due to **random variation**, even if both statins were equally effective.
*There is a 95% chance that the difference in reduction of LDL observed reflects a real difference between the two groups*
- This statement is an incorrect interpretation of the p-value; it confuses the p-value with the **probability that the alternative hypothesis is true**.
- A p-value does not directly tell us the probability that the observed difference is "real" or due to the intervention being studied.
*Though A is more effective than B, there is a 5% chance the difference in reduction of LDL between the two groups is due to chance*
- This statement implies that Statin A is more effective, which cannot be concluded with a p-value of 0.052 if the significance level (alpha) was set at 0.05.
- While it's true there's a chance the difference is due to chance, claiming A is "more effective" based on this p-value before statistical significance is usually declared is misleading.
*If 100 permutations of this experiment were conducted, 5 of them would show similar results to those described above*
- This is an incorrect interpretation. The p-value does not predict the outcome of repeated experiments in this manner.
- It refers to the **probability under the null hypothesis in a single experiment**, not the frequency of results across multiple hypothetical repetitions.
*This is a statistically significant result*
- A p-value of 0.052 is generally considered **not statistically significant** if the conventional alpha level (significance level) is set at 0.05 (or 5%).
- For a result to be statistically significant at alpha = 0.05, the p-value must be **less than 0.05**.
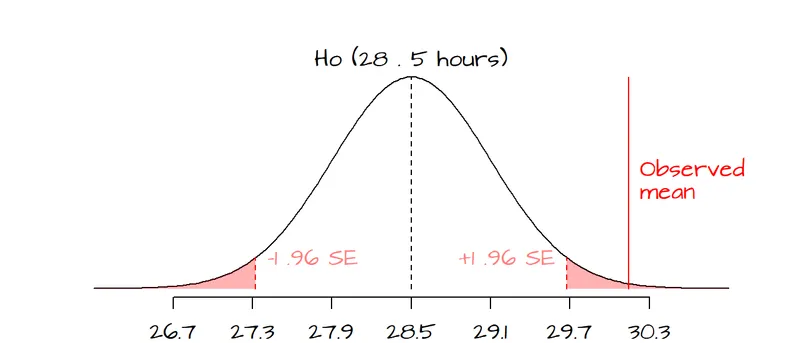
Clinical vs statistical significance US Medical PG Question 3: A randomized control double-blind study is conducted on the efficacy of 2 sulfonylureas. The study concluded that medication 1 was more efficacious in lowering fasting blood glucose than medication 2 (p ≤ 0.05; 95% CI: 14 [10-21]). Which of the following is true regarding a 95% confidence interval (CI)?
- A. If the same study were repeated multiple times, approximately 95% of the calculated confidence intervals would contain the true population parameter. (Correct Answer)
- B. The 95% confidence interval is the probability chosen by the researcher to be the threshold of statistical significance.
- C. When a 95% CI for the estimated difference between groups contains the value ‘0’, the results are significant.
- D. It represents the probability that chance would not produce the difference shown, 95% of the time.
- E. The study is adequately powered at the 95% confidence interval.
Clinical vs statistical significance Explanation: ***If the same study were repeated multiple times, approximately 95% of the calculated confidence intervals would contain the true population parameter.***
- This statement accurately defines the **frequentist interpretation** of a confidence interval (CI). It reflects the long-run behavior of the CI over hypothetical repetitions of the study.
- A 95% CI means that if you were to repeat the experiment many times, 95% of the CIs calculated from those experiments would capture the **true underlying population parameter**.
*The 95% confidence interval is the probability chosen by the researcher to be the threshold of statistical significance.*
- The **alpha level (α)**, typically set at 0.05 (or 5%), is the threshold for statistical significance (p ≤ 0.05), representing the probability of a Type I error.
- The 95% confidence level (1-α) is related to statistical significance, but it is not the *threshold* itself; rather, it indicates the **reliability** of the interval estimate.
*When a 95% CI for the estimated difference between groups contains the value ‘0’, the results are significant.*
- If a 95% CI for the difference between groups **contains 0**, it implies that there is **no statistically significant difference** between the groups at the 0.05 alpha level.
- A statistically significant difference (p ≤ 0.05) would be indicated if the 95% CI **does NOT contain 0**, suggesting that the intervention had a real effect.
*It represents the probability that chance would not produce the difference shown, 95% of the time.*
- This statement misinterprets the meaning of a CI and probability. The chance of not producing the observed difference is typically addressed by the **p-value**, not directly by the CI in this manner.
- A CI provides a **range of plausible values** for the population parameter, not a probability about the role of chance in producing the observed difference.
*The study is adequately powered at the 95% confidence interval.*
- **Statistical power** is the probability of correctly rejecting a false null hypothesis, typically set at 80% or 90%. It is primarily determined by sample size, effect size, and alpha level.
- A 95% CI is a measure of the **precision** of an estimate, while power refers to the **ability of a study to detect an effect** if one exists. They are related but distinct concepts.
Clinical vs statistical significance US Medical PG Question 4: You are reading through a recent article that reports significant decreases in all-cause mortality for patients with malignant melanoma following treatment with a novel biological infusion. Which of the following choices refers to the probability that a study will find a statistically significant difference when one truly does exist?
- A. Type II error
- B. Type I error
- C. Confidence interval
- D. p-value
- E. Power (Correct Answer)
Clinical vs statistical significance Explanation: ***Power***
- **Power** is the probability that a study will correctly reject the null hypothesis when it is, in fact, false (i.e., will find a statistically significant difference when one truly exists).
- A study with high power minimizes the risk of a **Type II error** (failing to detect a real effect).
*Type II error*
- A **Type II error** (or **beta error**) occurs when a study fails to reject a false null hypothesis, meaning it concludes there is no significant difference when one actually exists.
- This is the **opposite** of what the question describes, which asks for the probability of *finding* a difference.
*Type I error*
- A **Type I error** (or **alpha error**) occurs when a study incorrectly rejects a true null hypothesis, concluding there is a significant difference when one does not actually exist.
- This relates to the **p-value** and the level of statistical significance (e.g., p < 0.05).
*Confidence interval*
- A **confidence interval** provides a range of values within which the true population parameter is likely to lie with a certain degree of confidence (e.g., 95%).
- It does not directly represent the probability of finding a statistically significant difference when one truly exists.
*p-value*
- The **p-value** is the probability of observing data as extreme as, or more extreme than, that obtained in the study, assuming the null hypothesis is true.
- It is used to determine statistical significance, but it is not the probability of detecting a true effect.
Clinical vs statistical significance US Medical PG Question 5: A research group wants to assess the safety and toxicity profile of a new drug. A clinical trial is conducted with 20 volunteers to estimate the maximum tolerated dose and monitor the apparent toxicity of the drug. The study design is best described as which of the following phases of a clinical trial?
- A. Phase 0
- B. Phase III
- C. Phase V
- D. Phase II
- E. Phase I (Correct Answer)
Clinical vs statistical significance Explanation: ***Phase I***
- **Phase I clinical trials** involve a small group of healthy volunteers (typically 20-100) to primarily assess **drug safety**, determine a safe dosage range, and identify side effects.
- The main goal is to establish the **maximum tolerated dose (MTD)** and evaluate the drug's pharmacokinetic and pharmacodynamic profiles.
*Phase 0*
- **Phase 0 trials** are exploratory studies conducted in a very small number of subjects (10-15) to gather preliminary data on a drug's **pharmacodynamics and pharmacokinetics** in humans.
- They involve microdoses, not intended to have therapeutic effects, and thus cannot determine toxicity or MTD.
*Phase III*
- **Phase III trials** are large-scale studies involving hundreds to thousands of patients to confirm the drug's **efficacy**, monitor side effects, compare it to standard treatments, and collect information that will allow the drug to be used safely.
- These trials are conducted after safety and initial efficacy have been established in earlier phases.
*Phase V*
- "Phase V" is not a standard, recognized phase in the traditional clinical trial classification (Phase 0, I, II, III, IV).
- This term might be used in some non-standard research contexts or for post-marketing studies that go beyond Phase IV surveillance, but it is not a formal phase for initial drug development.
*Phase II*
- **Phase II trials** involve several hundred patients with the condition the drug is intended to treat, focusing on **drug efficacy** and further evaluating safety.
- While safety is still monitored, the primary objective shifts to determining if the drug works for its intended purpose and at what dose.
Clinical vs statistical significance US Medical PG Question 6: You submit a paper to a prestigious journal about the effects of coffee consumption on mesothelioma risk. The first reviewer lauds your clinical and scientific acumen, but expresses concern that your study does not have adequate statistical power. Statistical power refers to which of the following?
- A. The probability of detecting an association when no association exists.
- B. The probability of not detecting an association when an association does exist.
- C. The probability of detecting an association when an association does exist. (Correct Answer)
- D. The first derivative of work.
- E. The square root of the variance.
Clinical vs statistical significance Explanation: ***The probability of detecting an association when an association does exist.***
- **Statistical power** is defined as the probability that a study will correctly reject a false null hypothesis, meaning it will detect a true effect or association if one exists.
- A study with **adequate statistical power** is less likely to miss a real effect.
*The probability of detecting an association when no association exists.*
- This describes a **Type I error** or **false positive**, often represented by **alpha (α)**.
- It is the probability of incorrectly concluding an effect or association exists when, in reality, there is none.
*The probability of not detecting an association when an association does exist.*
- This refers to a **Type II error** or **false negative**, represented by **beta (β)**.
- **Statistical power** is calculated as **1 - β**, so this option describes the complement of power.
*The first derivative of work.*
- The first derivative of work with respect to time represents **power** in physics, which is the rate at which work is done.
- This option is a **distractor** from physics and is unrelated to statistical power in research.
*The square root of the variance.*
- The **square root of the variance** is the **standard deviation**, a measure of the dispersion or spread of data.
- This is a statistical concept but is not the definition of statistical power.
Clinical vs statistical significance US Medical PG Question 7: You are currently employed as a clinical researcher working on clinical trials of a new drug to be used for the treatment of Parkinson's disease. Currently, you have already determined the safe clinical dose of the drug in a healthy patient. You are in the phase of drug development where the drug is studied in patients with the target disease to determine its efficacy. Which of the following phases is this new drug currently in?
- A. Phase 4
- B. Phase 1
- C. Phase 2 (Correct Answer)
- D. Phase 0
- E. Phase 3
Clinical vs statistical significance Explanation: ***Phase 2***
- **Phase 2 trials** involve studying the drug in patients with the target disease to assess its **efficacy** and further evaluate safety, typically involving a few hundred patients.
- The question describes a stage after safe dosing in healthy patients (Phase 1) and before large-scale efficacy confirmation (Phase 3), focusing on efficacy in the target population.
*Phase 4*
- **Phase 4 trials** occur **after a drug has been approved** and marketed, monitoring long-term effects, optimal use, and rare side effects in a diverse patient population.
- This phase is conducted post-market approval, whereas the question describes a drug still in development prior to approval.
*Phase 1*
- **Phase 1 trials** primarily focus on determining the **safety and dosage** of a new drug in a **small group of healthy volunteers** (or sometimes patients with advanced disease if the drug is highly toxic).
- The question states that the safe clinical dose in a healthy patient has already been determined, indicating that Phase 1 has been completed.
*Phase 0*
- **Phase 0 trials** are exploratory, very early-stage studies designed to confirm that the drug reaches the target and acts as intended, typically involving a very small number of doses and participants.
- These trials are conducted much earlier in the development process, preceding the determination of safe clinical doses and large-scale efficacy studies.
*Phase 3*
- **Phase 3 trials** are large-scale studies involving hundreds to thousands of patients to confirm **efficacy**, monitor side effects, compare it to commonly used treatments, and collect information that will allow the drug to be used safely.
- While Phase 3 does assess efficacy, it follows Phase 2 and is typically conducted on a much larger scale before submitting for regulatory approval.
Clinical vs statistical significance US Medical PG Question 8: Two research groups independently study the same genetic variant's association with diabetes. Study A (n=5,000) reports OR=1.25, 95% CI: 1.05-1.48, p=0.01. Study B (n=50,000) reports OR=1.08, 95% CI: 1.02-1.14, p=0.006. Both studies are methodologically sound. Synthesize these findings to determine the most likely true effect and evaluate implications for clinical and research interpretation.
- A. Study B is definitive because of its larger sample size and should replace Study A's findings
- B. The study with the lower p-value (Study B) is automatically more reliable
- C. The studies are contradictory and no conclusions can be drawn
- D. Study A is correct because it was published first
- E. The true effect is likely modest (closer to Study B's estimate); Study A likely overestimated due to smaller sample size, but both show statistical significance with clinically marginal effects (Correct Answer)
Clinical vs statistical significance Explanation: ***The true effect is likely modest (closer to Study B's estimate); Study A likely overestimated due to smaller sample size, but both show statistical significance with clinically marginal effects***
- Study B has significantly higher **statistical power** and **precision** (narrower 95% CI) due to its larger sample size, making its **odds ratio (OR)** estimate more reliable.
- Smaller initial studies often exhibit the **Winner's Curse**, where effect sizes are **overestimated** to reach the threshold for statistical significance.
*Study A is correct because it was published first*
- **Publication order** does not determine the scientific validity or accuracy of genetic association studies.
- Early studies are more prone to **random error** and inflated effect sizes compared to later, larger-scale replications.
*Study B is definitive because of its larger sample size and should replace Study A's findings*
- While Study B is more **precise**, both studies are directionally consistent and both show **statistical significance** (p < 0.05).
- Scientific evidence is **cumulative**; Study B refines and confirms the existence of an association rather than declaring Study A's findings as entirely false.
*The studies are contradictory and no conclusions can be drawn*
- The studies are not contradictory because both **confidence intervals** show an OR > 1.0, and both reach **statistical significance**.
- Both groups found the same **direction of effect**, suggesting a real albeit modest genetic association with diabetes.
*The study with the lower p-value (Study B) is automatically more reliable*
- Reliability depends on **methodological rigor** and **precision**, whereas the p-value is heavily influenced by **sample size**.
- A lower p-value indicates stronger evidence against the **null hypothesis** but does not inherently mean the study is free from bias or more reliable in its effect estimate.
Clinical vs statistical significance US Medical PG Question 9: A prestigious journal publishes a trial showing a new cancer drug extends survival by 2 months (p=0.001, 95% CI: 1.5-2.5 months). The drug costs $150,000 per patient and causes Grade 3-4 toxicity in 60% of patients. Three prior unpublished trials showed non-significant results (all p>0.20). Synthesize these findings to evaluate the evidence base.
- A. This pattern suggests publication bias; the significant result may be a false positive among multiple trials, and the modest benefit must be weighed against substantial toxicity and cost (Correct Answer)
- B. The confidence interval proves the drug should be standard of care
- C. P-values below 0.01 override concerns about prior negative studies
- D. The published study's highly significant p-value validates the drug's efficacy
- E. The three unpublished trials are irrelevant to evaluating the published study
Clinical vs statistical significance Explanation: ***This pattern suggests publication bias; the significant result may be a false positive among multiple trials, and the modest benefit must be weighed against substantial toxicity and cost***
- The existence of three unpublished negative trials alongside one positive one strongly indicates **publication bias** (the file drawer effect), suggesting the positive result might be a **Type I error** or an overestimation.
- **Statistical significance** (p=0.001) does not equal **clinical significance**; a marginal 2-month survival gain must be balanced against extreme **financial cost** and a 60% rate of **Grade 3-4 toxicity**.
*The published study's highly significant p-value validates the drug's efficacy*
- A **low p-value** only indicates that the null hypothesis is unlikely within that specific trial; it does not account for the **context** of other failed experiments.
- Efficacy cannot be validated in isolation when the broader **evidence base** (including unpublished data) shows inconsistent results.
*The three unpublished trials are irrelevant to evaluating the published study*
- All relevant clinical trials must be synthesized via **meta-analysis** or systematic review to determine the true **effect size** of an intervention.
- Ignoring unpublished data leads to **evidence distortion**, where clinicians perceive a drug as more effective than it truly is.
*P-values below 0.01 override concerns about prior negative studies*
- No **p-value** can magically override the **prior probability** of a drug's success; consistent negative results in prior trials increase the likelihood that a later positive result is a **false positive**.
- High-impact medical decisions require a consistent **body of evidence** rather than a single outlier result, regardless of the level of significance.
*The confidence interval proves the drug should be standard of care*
- The **95% Confidence Interval** (1.5–2.5 months) tells us only about the **precision** of the measurement, not the **magnitude of clinical benefit**.
- Becoming a **standard of care** requires a favorable **risk-benefit ratio**, which is undermined here by severe **adverse events** and poor **cost-effectiveness**.
Clinical vs statistical significance US Medical PG Question 10: A pharmaceutical company conducts 20 different analyses on their trial data, testing for effects on various secondary outcomes. One analysis shows a significant benefit (p=0.03) on hospital readmission rates. The primary outcome (mortality) showed p=0.12. The company seeks FDA approval based on the readmission data. Evaluate the validity and implications of this approach.
- A. Secondary outcomes are more important than primary outcomes when significant
- B. The p=0.03 result is valid and supports approval regardless of the primary outcome
- C. Any p<0.05 in a clinical trial justifies approval
- D. This represents multiple testing without correction, inflating Type I error; the significant result may be due to chance and selective reporting (Correct Answer)
- E. The mortality p-value of 0.12 is close enough to significance to support both findings
Clinical vs statistical significance Explanation: ***This represents multiple testing without correction, inflating Type I error; the significant result may be due to chance and selective reporting***
- Performing **multiple comparisons** (20 analyses) without adjustment increases the probability of a **false positive** result; by chance alone, 1 out of 20 tests is expected to be significant at p < 0.05.
- Reliable conclusions require **post-hoc corrections** (like Bonferroni) or pre-specified hierarchies to prevent **selective reporting** or "p-hacking" of secondary outcomes.
*The p=0.03 result is valid and supports approval regardless of the primary outcome*
- A result is not considered valid in isolation when it is one of many tests; the **Type I error rate** is not maintained at 5%.
- Regulatory approval usually requires the **primary outcome** to be met, as secondary outcomes are generally considered **hypothesis-generating**.
*Secondary outcomes are more important than primary outcomes when significant*
- **Primary outcomes** are the pre-defined measures that the trial is specifically powered to detect; ignoring them leads to **bias**.
- Significance in a **secondary outcome** cannot supersede a non-significant primary outcome, especially when the test wasn't protected against multiple comparisons.
*The mortality p-value of 0.12 is close enough to significance to support both findings*
- In frequentist statistics, a **p-value of 0.12** is greater than the standard threshold of 0.05 and must be interpreted as **not statistically significant**.
- "Close" results do not validate other weak findings; they suggest the study failed to reject the **null hypothesis** for the most important clinical endpoint.
*Any p<0.05 in a clinical trial justifies approval*
- Approval requires evidence of both **statistical significance** and **clinical relevance**, typically demonstrated in the primary endpoint.
- **Spurious correlations** occur frequently in large datasets; therefore, a single p < 0.05 obtained through **data dredging** is insufficient for regulatory standards.
More Clinical vs statistical significance US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.