A randomized control double-blind study is conducted on the efficacy of 2 sulfonylureas. The study concluded that medication 1 was more efficacious in lowering fasting blood glucose than medication 2 (p ≤ 0.05; 95% CI: 14 [10-21]). Which of the following is true regarding a 95% confidence interval (CI)?

If the same study were repeated multiple times, approximately 95% of the calculated confidence intervals would contain the true population parameter.

The 95% confidence interval is the probability chosen by the researcher to be the threshold of statistical significance.

When a 95% CI for the estimated difference between groups contains the value ‘0’, the results are significant.

It represents the probability that chance would not produce the difference shown, 95% of the time.

The study is adequately powered at the 95% confidence interval.

A 28-year-old male presents to his primary care physician with complaints of intermittent abdominal pain and alternating bouts of constipation and diarrhea. His medical chart is not significant for any past medical problems or prior surgeries. He is not prescribed any current medications. Which of the following questions would be the most useful next question in eliciting further history from this patient?

"Can you tell me more about the symptoms you have been experiencing?"

"Does the diarrhea typically precede the constipation, or vice-versa?"

"Is the diarrhea foul-smelling?"

"Please rate your abdominal pain on a scale of 1-10, with 10 being the worst pain of your life"

"Are the symptoms worse in the morning or at night?"

P-values and confidence intervals | Biostatistics

📊 Statistical Precision: The Evidence Architecture

You'll master the twin pillars that transform raw data into clinical decisions: p-values reveal whether observed effects are likely real or mere chance, while confidence intervals define the plausible range and magnitude of those effects. Together, they form your evidence architecture for interpreting studies, distinguishing statistical noise from genuine signals, and determining whether findings matter enough to change practice. This lesson builds your fluency in reading the statistical language that underpins every treatment guideline, diagnostic test, and therapeutic choice you'll make.

📌 Remember: PANIC for P-value interpretation - Probability of observing data, Assuming null hypothesis true, Not probability null is true, Influenced by sample size, Cannot prove causation

Statistical Foundation Architecture

The statistical evidence hierarchy operates through interconnected probability frameworks:

P-values (α = 0.05 standard)
- Probability of observing data assuming null hypothesis true
- Type I error rate: 5% false positive threshold
  - Medical research standard: p < 0.05
  - High-stakes decisions: p < 0.01 or p < 0.001
  - Bonferroni correction: α/n for multiple comparisons
Confidence Intervals (95% standard)
- Range containing true parameter with 95% probability
- Width inversely related to sample size and precision
  - Narrow CI: High precision, large sample
  - Wide CI: Low precision, small sample
  - Margin of error = Critical value × Standard error

⭐ Clinical Pearl: A 95% CI that excludes the null value corresponds to p < 0.05 in two-tailed testing. When CI includes null value, p > 0.05 indicates insufficient evidence against null hypothesis.

Statistical Measure	Threshold	Clinical Interpretation	Sample Size Impact	Error Type
P-value	< 0.05	Statistically significant	Smaller p with larger n	Type I (α)
95% CI	Excludes null	Clinically meaningful range	Narrower with larger n	Type II (β)
99% CI	Wider range	Higher confidence level	2.6× wider than 95%	Reduced Type I
Power	≥ 80%	Adequate sample size	Increases with larger n	Type II (1-β)
Effect size	Cohen's d > 0.5	Moderate clinical impact	Independent of sample size	Clinical significance

The precision of statistical inference depends on sample size (n), effect size (δ), and variability (σ). Standard error decreases proportionally to √n, making larger studies exponentially more precise. Power analysis requires α = 0.05, β = 0.20 (80% power), effect size estimation, and population variance to determine adequate sample size.

Connect these statistical foundations through hypothesis testing frameworks to understand how p-values and confidence intervals work together in clinical decision-making.

📊 Statistical Precision: The Evidence Architecture

Definition and interpretation of p-values

Confidence interval construction

🎯 Hypothesis Testing: The Clinical Decision Engine

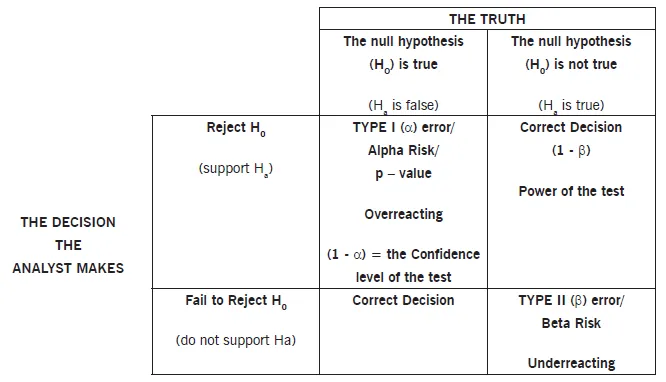
Hypothesis testing decision tree with Type I and Type II errors

📌 Remember: HATS for Hypothesis Testing - H₀ assumes no difference, Alternative claims difference exists, Type I rejects true null, Statistical power detects true alternatives

Decision Framework Architecture

The hypothesis testing machinery operates through systematic error control:

Null Hypothesis (H₀): No difference or no effect
- Default assumption requiring evidence to overturn
- Conservative approach: Maintains status quo until proven otherwise
  - Drug trials: New treatment = Standard treatment
  - Diagnostic tests: Test accuracy = Chance level
  - Risk factors: Exposure = No increased risk
Alternative Hypothesis (H₁): Difference exists or effect present
- Research hypothesis requiring statistical evidence
- Directional claims supported by data analysis
  - Two-tailed: μ₁ ≠ μ₂ (difference in either direction)
  - One-tailed: μ₁ > μ₂ or μ₁ < μ₂ (specific direction)

⭐ Clinical Pearl: Type I error (α) represents false positive rate - concluding treatment works when it doesn't. Type II error (β) represents false negative rate - missing real treatment effects. Power = 1-β measures ability to detect true effects.

Error Type	Definition	Clinical Consequence	Control Method	Typical Rate
Type I (α)	False Positive	Adopt ineffective treatment	Set α level	5%
Type II (β)	False Negative	Miss effective treatment	Increase sample size	20%
Power (1-β)	True Positive	Detect real effects	Adequate sample size	80%
Specificity	True Negative	Correctly reject null	Proper study design	95%
Sensitivity	True Positive	Detect true alternatives	Sufficient power	80%

Statistical power depends on four interconnected factors: effect size (larger effects easier to detect), sample size (more data increases power), significance level (lower α reduces power), and population variability (less noise increases power). Power analysis calculates required sample size to achieve 80% power for detecting clinically meaningful differences at α = 0.05.

Connect hypothesis testing logic through p-value interpretation principles to understand how probability calculations support clinical decision-making.

🎯 Hypothesis Testing: The Clinical Decision Engine

One-sided vs two-sided tests

Relationship between CIs and hypothesis testing

🔍 P-Value Mastery: The Probability Decoder

📌 Remember: PROVE for P-value interpretation - Probability of data given H₀, Random sampling assumption, One-time calculation, Varies with sample size, Evidence strength not effect size

Probability Calculation Framework

P-values represent conditional probabilities calculated under specific statistical assumptions:

P-value Definition: P(Data | H₀ true)
- Probability of observing current data or more extreme
- Assumes null hypothesis is true throughout calculation
  - NOT probability that null hypothesis is true
  - NOT probability of replication in future studies
  - NOT measure of clinical importance or effect size
Calculation Process: Test statistic → Probability distribution → P-value
- Z-test: Standard normal distribution for large samples
- T-test: Student's t-distribution for small samples (n < 30)
  - Degrees of freedom = n-1 for one-sample tests
  - Degrees of freedom = n₁+n₂-2 for two-sample tests

⭐ Clinical Pearl: P-values decrease with larger sample sizes even for identical effect sizes. A clinically trivial difference can achieve p < 0.001 with sufficient sample size, while clinically important differences may show p > 0.05 in underpowered studies.

P-value Range	Evidence Strength	Clinical Interpretation	Replication Probability	Decision Framework
p < 0.001	Very Strong	Highly unlikely under H₀	>95% replication	Strong evidence against H₀
p < 0.01	Strong	Unlikely under H₀	>90% replication	Good evidence against H₀
p < 0.05	Moderate	Somewhat unlikely under H₀	>80% replication	Sufficient evidence against H₀
p = 0.05-0.10	Weak	Borderline evidence	50-80% replication	Insufficient evidence
p > 0.10	None	Consistent with H₀	<50% replication	No evidence against H₀

Common p-value misconceptions include: P(H₀|Data) confusion (Bayesian posterior probability), replication probability misinterpretation, effect size conflation, and clinical significance assumption. P-values measure evidence strength against null hypothesis under frequentist probability framework, not probability of hypotheses or clinical importance.

Sample size effects create p-value paradoxes: underpowered studies miss clinically important effects (Type II errors), while overpowered studies detect clinically trivial differences (statistical significance without clinical relevance). Effect size measures (Cohen's d, odds ratios, mean differences) provide clinical magnitude independent of sample size.

Connect p-value interpretation through confidence interval construction to understand how range estimates complement point probability calculations.

🔍 P-Value Mastery: The Probability Decoder

Common misinterpretations of p-values

P-value controversy and alternatives

📏 Confidence Intervals: The Precision Boundary System

📌 Remember: CRIME for CI interpretation - Contains true parameter 95% of time, Range of plausible values, Inverse relationship with sample size, Margin of error calculation, Excludes null means significant

Interval Construction Architecture

Confidence interval construction follows mathematical precision with clinical interpretation:

95% Confidence Interval: Point Estimate ± Margin of Error
- Margin of Error = Critical Value × Standard Error
- Standard Error decreases with √n (square root of sample size)
  - Larger samples → Smaller standard errors → Narrower intervals
  - Higher confidence levels → Larger critical values → Wider intervals
  - Greater variability → Larger standard errors → Wider intervals
Critical Values depend on distribution and confidence level:
- Z-distribution: ±1.96 for 95% CI, ±2.58 for 99% CI
- T-distribution: Varies by degrees of freedom (larger for smaller samples)

⭐ Clinical Pearl: 95% CI means if we repeated the study 100 times, approximately 95 intervals would contain the true parameter value. The specific interval from our study either contains the true value (probability = 1) or doesn't (probability = 0).

Parameter Type	Formula	Critical Value	Interpretation	Clinical Application
Mean (large n)	x̄ ± 1.96(σ/√n)	Z = 1.96	Average value range	Blood pressure, lab values
Mean (small n)	x̄ ± t(s/√n)	t varies by df	Average with uncertainty	Small clinical trials
Proportion	p̂ ± 1.96√(p̂q̂/n)	Z = 1.96	Percentage range	Disease prevalence, cure rates
Difference	(x̄₁-x̄₂) ± t(SE)	t varies by df	Treatment effect range	Drug efficacy comparisons
Odds Ratio	exp(ln(OR) ± 1.96×SE)	Z = 1.96	Risk ratio range	Case-control studies

Confidence level interpretation: 95% confidence refers to the long-run frequency of intervals containing true parameters, not the probability that our specific interval contains the true value. Higher confidence levels (99%) create wider intervals with greater certainty of capturing true parameters.

Relationship to hypothesis testing: When 95% CI excludes null value, p < 0.05 for two-tailed test. When 95% CI includes null value, p > 0.05 indicates insufficient evidence. CI width provides precision information that p-values cannot convey.

Connect confidence interval precision through clinical significance assessment to understand how statistical ranges translate into meaningful medical decisions.

📏 Confidence Intervals: The Precision Boundary System

Effect sizes and confidence intervals

Confidence intervals for non-parametric tests

⚖️ Clinical Significance: The Medical Relevance Filter

Clinical versus statistical significance comparison with effect sizes

📌 Remember: SCALE for Clinical Significance - Size of effect matters, Cost-benefit analysis, Applicability to patients, Long-term outcomes, Ethical considerations

Medical Relevance Framework

Clinical significance evaluation requires multi-dimensional assessment beyond statistical calculations:

Effect Size Measures quantify practical importance:
- Cohen's d: Standardized mean difference (0.2 small, 0.5 medium, 0.8 large)
- Number Needed to Treat (NNT): 1/Absolute Risk Reduction
  - NNT = 2-5: Highly effective interventions
  - NNT = 6-10: Moderately effective interventions
  - NNT > 20: Questionable clinical value
- Minimal Clinically Important Difference (MCID): Patient-perceived benefit
Clinical Context Factors:
- Baseline risk of patient population
- Alternative treatment options and comparative effectiveness
- Adverse effects and risk-benefit ratio
- Cost-effectiveness and resource allocation

⭐ Clinical Pearl: Large studies can detect statistically significant but clinically trivial differences. Small studies may miss clinically important but statistically non-significant effects. Effect size and confidence intervals provide better clinical guidance than p-values alone.

Scenario	Statistical Result	Effect Size	Clinical Interpretation	Clinical Decision
Large RCT	p < 0.001	Small (d = 0.1)	Statistically significant, clinically trivial	Do not implement
Small RCT	p = 0.12	Large (d = 0.9)	Not significant, clinically important	Consider larger study
Meta-analysis	p < 0.05	Medium (d = 0.5)	Significant and meaningful	Implement with monitoring
Pilot study	p = 0.08	Very large (d = 1.2)	Borderline significance, major effect	Proceed to full trial
Registry study	p < 0.0001	Trivial (d = 0.05)	Highly significant, no clinical value	Academic interest only

Minimal Clinically Important Differences vary by condition and outcome measure: Pain scales (1-2 points on 10-point scale), Quality of life (0.5 standard deviations), Blood pressure (5-10 mmHg for cardiovascular outcomes), HbA1c (0.5% for diabetes management). Patient-reported outcomes often define clinical relevance better than biomarker changes.

Cost-effectiveness analysis integrates clinical benefits with economic considerations: Quality-Adjusted Life Years (QALYs), Incremental Cost-Effectiveness Ratios (ICERs), and budget impact determine healthcare implementation decisions beyond statistical significance.

Connect clinical significance assessment through systematic integration frameworks to understand how multiple statistical and clinical factors combine in evidence-based medicine.

⚖️ Clinical Significance: The Medical Relevance Filter

Clinical vs statistical significance

🔗 Evidence Integration: The Multi-Dimensional Assessment Matrix

📌 Remember: MERGE for Evidence Integration - Meta-analysis synthesis, Effect size consistency, Risk of bias assessment, GRADE quality rating, External validity evaluation

Multi-Dimensional Assessment Architecture

Evidence synthesis requires systematic evaluation across multiple quality dimensions:

Statistical Synthesis Methods:
- Fixed-effects models: Assume single true effect across studies
- Random-effects models: Allow effect variation between studies
  - I² statistic: 0-25% low heterogeneity, 50-75% moderate, >75% high
  - Tau²: Between-study variance in random-effects models
  - Q-statistic: Chi-square test for heterogeneity (p < 0.10 suggests heterogeneity)
Publication Bias Assessment:
- Funnel plot asymmetry: Visual inspection for missing studies
- Egger's test: Statistical test for small-study effects (p < 0.05 suggests bias)
- Trim-and-fill method: Imputes missing studies and adjusts effect estimates

⭐ Clinical Pearl: High heterogeneity (I² > 75%) suggests important differences between studies in populations, interventions, or outcomes. Subgroup analysis and meta-regression can explore sources of heterogeneity and identify patient-specific effects.

Evidence Component	Assessment Method	Quality Indicators	Clinical Impact	Decision Weight
Statistical Power	Sample size calculation	>80% power	Adequate effect detection	High
Risk of Bias	Cochrane RoB tool	Low risk domains	Internal validity	Very High
Heterogeneity	I² and Tau²	<50% I²	Consistency across studies	High
Publication Bias	Funnel plots, Egger's	Symmetric distribution	Complete evidence base	Moderate
External Validity	PICO assessment	Representative populations	Generalizability	High

Network meta-analysis enables indirect comparisons between treatments never directly compared, using transitivity assumptions and consistency evaluation. Surface Under Cumulative Ranking (SUCRA) provides probabilistic rankings of treatment effectiveness across multiple interventions.

Real-world evidence integration combines randomized trial efficacy with observational study effectiveness, registry data, and electronic health records to assess pragmatic treatment effects in diverse patient populations with complex comorbidities.

Connect evidence integration through rapid clinical reference tools to transform comprehensive assessments into practical decision-making frameworks.

🔗 Evidence Integration: The Multi-Dimensional Assessment Matrix

Multiple comparison problem

Reporting standards in medical journals

🎯 Clinical Decision Mastery: The Rapid Assessment Toolkit

📌 Remember: RAPID for Clinical Decisions - Risk stratification, Assess pre-test probability, Post-test probability calculation, Integrate patient factors, Decision with uncertainty quantification

Essential Clinical Arsenal

Statistical Thresholds for Immediate Application:

P-value Interpretation Hierarchy:
- p < 0.001: Overwhelming evidence - implement immediately
- p < 0.01: Strong evidence - adopt with monitoring
- p < 0.05: Moderate evidence - consider patient factors
- p = 0.05-0.10: Weak evidence - individualize decisions
- p > 0.10: Insufficient evidence - maintain current practice
Confidence Interval Clinical Rules:
- Narrow CI excluding null: High precision, strong evidence
- Wide CI excluding null: Low precision, uncertain magnitude
- CI including null: Insufficient evidence regardless of width
- CI width > 2× MCID: Clinically uninformative precision

⭐ Clinical Pearl: Number Needed to Treat (NNT) provides immediate clinical relevance: NNT = 2 means 1 in 2 patients benefit, NNT = 10 means 1 in 10 patients benefit. NNT confidence intervals quantify uncertainty in treatment effectiveness.

Clinical Scenario	Statistical Evidence	Decision Framework	Action Threshold	Monitoring Plan
Life-threatening	p < 0.05, NNT < 10	Immediate implementation	>50% benefit probability	Intensive monitoring
Chronic disease	p < 0.01, NNT < 20	Gradual implementation	>70% benefit probability	Regular assessment
Preventive care	p < 0.001, NNT < 50	Population-based	>80% benefit probability	Long-term tracking
Experimental	p < 0.05, wide CI	Research setting	>60% benefit probability	Continuous evaluation
Cost-intensive	p < 0.01, ICER favorable	Economic evaluation	Cost-effective threshold	Budget impact analysis

Rapid Evidence Assessment Protocol: Study design hierarchy (RCT > cohort > case-control), sample size adequacy (power >80%), effect size magnitude (Cohen's d >0.5), confidence interval precision (excludes null), clinical applicability (similar population), and cost-effectiveness (acceptable ICER).

Clinical Uncertainty Management: Shared decision-making when evidence quality moderate, patient preference integration for value-sensitive decisions, trial of therapy for uncertain diagnoses, and safety-netting for low-probability serious conditions.

Understanding p-values and confidence intervals provides the statistical foundation for evidence-based medicine, enabling precise interpretation of research findings and confident clinical decision-making in complex patient care scenarios.