Reporting in medical literature US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Reporting in medical literature. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Reporting in medical literature US Medical PG Question 1: A researcher is investigating whether there is an association between the use of social media in teenagers and bipolar disorder. In order to study this potential relationship, she collects data from people who have bipolar disorder and matched controls without the disorder. She then asks how much on average these individuals used social media in the 3 years prior to their diagnosis. This continuous data is divided into 2 groups: those who used more than 2 hours per day and those who used less than 2 hours per day. She finds that out of 1000 subjects, 500 had bipolar disorder of which 300 used social media more than 2 hours per day. She also finds that 400 subjects who did not have the disorder also did not use social media more than 2 hours per day. Which of the following is the odds ratio for development of bipolar disorder after being exposed to more social media?
- A. 1.5
- B. 6 (Correct Answer)
- C. 0.17
- D. 0.67
Reporting in medical literature Explanation: ***6***
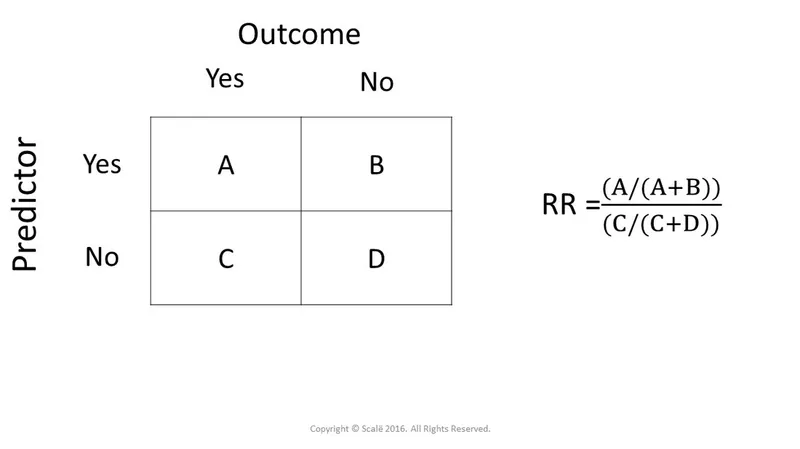
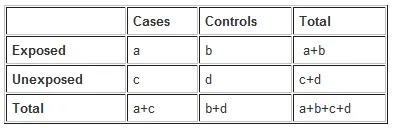
- To calculate the odds ratio, we first construct a 2x2 table [1]:
- Bipolar Disorder (Cases): 500
- No Bipolar Disorder (Controls): 500 (1000 total subjects - 500 cases)
- Cases exposed to more social media (>2 hrs/day): 300
- Cases not exposed to more social media (≤2 hrs/day): 200 (500 - 300)
- Controls not exposed to more social media (≤2 hrs/day): 400
- Controls exposed to more social media (>2 hrs/day): 100 (500 - 400)
- The odds ratio (OR) is calculated as (odds of exposure in cases) / (odds of exposure in controls) = (300/200) / (100/400) = 1.5 / 0.25 = **6** [1].
*1.5*
- This value represents the **odds of exposure** (more than 2 hours of social media) in individuals with bipolar disorder (300 cases exposed / 200 cases unexposed = 1.5).
- It is not the odds ratio, which compares these odds to the odds of exposure in the control group.
*0.17*
- This value is close to the reciprocal of 6 (1/6 ≈ 0.166), suggesting a potential miscalculation or an inverted odds ratio.
- An odds ratio of 0.17 would imply a protective effect (lower odds of bipolar disorder with more social media), which is contrary to the calculation and typical interpretation in this context.
*0.67*
- This value is the reciprocal of 1.5 (1/1.5 ≈ 0.67) which represents the odds of *not* being exposed in cases (200/300).
- It does not represent the correct odds ratio, which compares the odds of exposure in cases to the odds of exposure in controls.
Reporting in medical literature US Medical PG Question 2: Group of 100 medical students took an end of the year exam. The mean score on the exam was 70%, with a standard deviation of 25%. The professor states that a student's score must be within the 95% confidence interval of the mean to pass the exam. Which of the following is the minimum score a student can have to pass the exam?
- A. 45%
- B. 63.75%
- C. 67.5%
- D. 20%
- E. 65% (Correct Answer)
Reporting in medical literature Explanation: ***65%***
- To find the **95% confidence interval (CI) of the mean**, we use the formula: Mean ± (Z-score × Standard Error). For a 95% CI, the Z-score is approximately **1.96**.
- The **Standard Error (SE)** is calculated as SD/√n, where n is the sample size (100 students). So, SE = 25%/√100 = 25%/10 = **2.5%**.
- The 95% CI is 70% ± (1.96 × 2.5%) = 70% ± 4.9%. The lower bound is 70% - 4.9% = **65.1%**, which rounds to **65%** as the minimum passing score.
*45%*
- This value is significantly lower than the calculated lower bound of the 95% confidence interval (approximately 65.1%).
- It would represent a score far outside the defined passing range.
*63.75%*
- This value falls below the calculated lower bound of the 95% confidence interval (approximately 65.1%).
- While close, this score would not meet the professor's criterion for passing.
*67.5%*
- This value is within the 95% confidence interval (65.1% to 74.9%) but is **not the minimum score**.
- Lower scores within the interval would still qualify as passing.
*20%*
- This score is extremely low and falls significantly outside the 95% confidence interval for a mean of 70%.
- It would indicate performance far below the defined passing threshold.
Reporting in medical literature US Medical PG Question 3: A 25-year-old man with a genetic disorder presents for genetic counseling because he is concerned about the risk that any children he has will have the same disease as himself. Specifically, since childhood he has had difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy. He has also had diarrhea and malabsorption requiring enzyme replacement therapy. If his wife comes from a population where 1 in 10,000 people are affected by this same disorder, which of the following best represents the likelihood a child would be affected as well?
- A. 0.01%
- B. 2%
- C. 0.5%
- D. 1% (Correct Answer)
- E. 50%
Reporting in medical literature Explanation: ***Correct Option: 1%***
- The patient's symptoms (difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy; diarrhea and malabsorption requiring enzyme replacement therapy) are classic for **cystic fibrosis (CF)**, an **autosomal recessive disorder**.
- For an autosomal recessive disorder with a prevalence of 1 in 10,000 in the general population, **q² = 1/10,000**, so **q = 1/100 = 0.01**. The carrier frequency **(2pq)** is approximately **2q = 2 × (1/100) = 1/50 = 0.02**.
- The affected man is **homozygous recessive (aa)** and will always pass on the recessive allele. His wife has a **1/50 chance of being a carrier (Aa)**. If she is a carrier, she has a **1/2 chance of passing on the recessive allele**.
- Therefore, the probability of an affected child = **(Probability wife is a carrier) × (Probability wife passes recessive allele) = 1/50 × 1/2 = 1/100 = 1%**.
*Incorrect Option: 0.01%*
- This percentage is too low and does not correctly account for the carrier frequency in the population and the probability of transmission from a carrier mother.
*Incorrect Option: 2%*
- This represents approximately the carrier frequency (1/50 ≈ 2%), but does not account for the additional 1/2 probability that a carrier mother would pass on the recessive allele.
*Incorrect Option: 0.5%*
- This value would be correct if the carrier frequency were 1/100 instead of 1/50, which does not match the given population prevalence.
*Incorrect Option: 50%*
- **50%** would be the risk if both parents were carriers of an autosomal recessive disorder (1/4 chance = 25% for affected, but if we know one parent passes the allele, conditional probability changes). More accurately, 50% would apply if the disorder were **autosomal dominant** with one affected parent, which is not the case here.
Reporting in medical literature US Medical PG Question 4: A randomized control double-blind study is conducted on the efficacy of 2 sulfonylureas. The study concluded that medication 1 was more efficacious in lowering fasting blood glucose than medication 2 (p ≤ 0.05; 95% CI: 14 [10-21]). Which of the following is true regarding a 95% confidence interval (CI)?
- A. If the same study were repeated multiple times, approximately 95% of the calculated confidence intervals would contain the true population parameter. (Correct Answer)
- B. The 95% confidence interval is the probability chosen by the researcher to be the threshold of statistical significance.
- C. When a 95% CI for the estimated difference between groups contains the value ‘0’, the results are significant.
- D. It represents the probability that chance would not produce the difference shown, 95% of the time.
- E. The study is adequately powered at the 95% confidence interval.
Reporting in medical literature Explanation: ***If the same study were repeated multiple times, approximately 95% of the calculated confidence intervals would contain the true population parameter.***
- This statement accurately defines the **frequentist interpretation** of a confidence interval (CI). It reflects the long-run behavior of the CI over hypothetical repetitions of the study.
- A 95% CI means that if you were to repeat the experiment many times, 95% of the CIs calculated from those experiments would capture the **true underlying population parameter**.
*The 95% confidence interval is the probability chosen by the researcher to be the threshold of statistical significance.*
- The **alpha level (α)**, typically set at 0.05 (or 5%), is the threshold for statistical significance (p ≤ 0.05), representing the probability of a Type I error.
- The 95% confidence level (1-α) is related to statistical significance, but it is not the *threshold* itself; rather, it indicates the **reliability** of the interval estimate.
*When a 95% CI for the estimated difference between groups contains the value ‘0’, the results are significant.*
- If a 95% CI for the difference between groups **contains 0**, it implies that there is **no statistically significant difference** between the groups at the 0.05 alpha level.
- A statistically significant difference (p ≤ 0.05) would be indicated if the 95% CI **does NOT contain 0**, suggesting that the intervention had a real effect.
*It represents the probability that chance would not produce the difference shown, 95% of the time.*
- This statement misinterprets the meaning of a CI and probability. The chance of not producing the observed difference is typically addressed by the **p-value**, not directly by the CI in this manner.
- A CI provides a **range of plausible values** for the population parameter, not a probability about the role of chance in producing the observed difference.
*The study is adequately powered at the 95% confidence interval.*
- **Statistical power** is the probability of correctly rejecting a false null hypothesis, typically set at 80% or 90%. It is primarily determined by sample size, effect size, and alpha level.
- A 95% CI is a measure of the **precision** of an estimate, while power refers to the **ability of a study to detect an effect** if one exists. They are related but distinct concepts.
Reporting in medical literature US Medical PG Question 5: A researcher is conducting a study to compare fracture risk in male patients above the age of 65 who received annual DEXA screening to peers who did not receive screening. He conducts a randomized controlled trial in 900 patients, with half of participants assigned to each experimental group. The researcher ultimately finds similar rates of fractures in the two groups. He then notices that he had forgotten to include 400 patients in his analysis. Including the additional participants in his analysis would most likely affect the study's results in which of the following ways?
- A. Wider confidence intervals of results
- B. Increased probability of committing a type II error
- C. Decreased significance level of results
- D. Increased external validity of results
- E. Increased probability of rejecting the null hypothesis when it is truly false (Correct Answer)
Reporting in medical literature Explanation: ***Increased probability of rejecting the null hypothesis when it is truly false***
- Including more participants increases the **statistical power** of the study, making it more likely to detect a true effect if one exists.
- A higher sample size provides a more precise estimate of the population parameters, leading to a greater ability to **reject a false null hypothesis**.
*Wider confidence intervals of results*
- A larger sample size generally leads to **narrower confidence intervals**, as it reduces the standard error of the estimate.
- Narrower confidence intervals indicate **greater precision** in the estimation of the true population parameter.
*Increased probability of committing a type II error*
- A **Type II error** (false negative) occurs when a study fails to reject a false null hypothesis.
- Increasing the sample size typically **reduces the probability of a Type II error** because it increases statistical power.
*Decreased significance level of results*
- The **significance level (alpha)** is a pre-determined threshold set by the researcher before the study begins, typically 0.05.
- It is independent of sample size and represents the **acceptable probability of committing a Type I error** (false positive).
*Increased external validity of results*
- **External validity** refers to the generalizability of findings to other populations, settings, or times.
- While a larger sample size can enhance the representativeness of the study population, external validity is primarily determined by the **sampling method** and the study's design context, not just sample size alone.
Reporting in medical literature US Medical PG Question 6: A healthy 29-year-old nulligravid woman comes to the physician for genetic counseling prior to conception. Her brother has a disease that has resulted in infertility, a right-sided heart, and frequent sinus and ear infections. No other family members are affected. The intended father has no history of this disease. The population prevalence of this disease is 1 in 40,000. Which of the following best represents the chance that this patient’s offspring will develop her brother's disease?
- A. 25%
- B. 66%
- C. 0.2% (Correct Answer)
- D. 0.7%
- E. 1%
Reporting in medical literature Explanation: ***0.2%***
- The brother's symptoms (infertility, right-sided heart, frequent infections) are characteristic of **Kartagener syndrome**, a form of **primary ciliary dyskinesia (PCD)**, which has an **autosomal recessive** inheritance pattern.
- Since the patient's parents are obligate heterozygotes (carriers), the patient has a 2/3 chance of being a carrier. Given the population prevalence of 1/40,000 for an autosomal recessive disease, the carrier frequency (2pq) is approximately **2 x sqrt(1/40,000) = 2 x 1/200 = 1/100**. The chance of her child inheriting the disease is (2/3 chance of patient being carrier) x (1/100 chance of partner being carrier) x (1/4 chance of affected offspring) = 2/1200 ≈ **0.00166 or 0.166%**, which is closest to 0.2%.
*25%*
- This would be the risk if both parents were known carriers, and it represents the chance of an affected offspring from two heterozygotes.
- In this scenario, the woman's partner's carrier status is unknown and based on population prevalence, making the overall risk much lower.
*66%*
- This is the probability that the patient (the healthy sister of an affected individual with an autosomal recessive disease) is a **carrier**.
- This value alone does not account for the partner's carrier status or the final Mendelian inheritance probability (1/4) for an affected child.
*0.7%*
- This percentage is too high; it might result from incorrect calculation of the population carrier frequency or misapplication of probabilities.
- The correct carrier frequency for the partner is 1/100, which is significantly lower than what would lead to a 0.7% final risk.
*1%*
- This value is also too high and likely results from a miscalculation of either the carrier frequency or the overall probability.
- A 1% chance would suggest a much higher population carrier frequency or a different inheritance scenario.
Reporting in medical literature US Medical PG Question 7: In a randomized controlled trial studying a new treatment, the primary endpoint (mortality) occurred in 14.4% of the treatment group and 16.7% of the control group. Which of the following represents the number of patients needed to treat to save one life, based on the primary endpoint?
- A. 1/(0.144 - 0.167)
- B. 1/(0.167 - 0.144) (Correct Answer)
- C. 1/(0.300 - 0.267)
- D. 1/(0.267 - 0.300)
- E. 1/(0.136 - 0.118)
Reporting in medical literature Explanation: ***1/(0.167 - 0.144)***
- The **Number Needed to Treat (NNT)** is calculated as **1 / Absolute Risk Reduction (ARR)**.
- The **Absolute Risk Reduction (ARR)** is the difference between the event rate in the control group (16.7%) and the event rate in the treatment group (14.4%), which is **0.167 - 0.144**.
*1/(0.144 - 0.167)*
- This calculation represents 1 divided by the **Absolute Risk Increase**, which would be relevant if the treatment increased mortality.
- The **NNT should always be a positive value**, indicating the number of patients to treat to prevent one adverse event.
*1/(0.300 - 0.267)*
- This option uses arbitrary numbers (0.300 and 0.267) that do not correspond to the given **mortality rates** in the problem.
- It does not reflect the correct calculation for **absolute risk reduction** based on the provided data.
*1/(0.267 - 0.300)*
- This option also uses arbitrary numbers not derived from the problem's data, and it would result in a **negative value** for the denominator.
- The difference between event rates of 0.267 and 0.300 is not present in the given information for this study.
*1/(0.136 - 0.118)*
- This calculation uses arbitrary numbers (0.136 and 0.118) that are not consistent with the reported **mortality rates** of 14.4% and 16.7%.
- These values do not represent the **Absolute Risk Reduction** required for calculating NNT in this specific scenario.
Reporting in medical literature US Medical PG Question 8: In 2013 the national mean score on the USMLE Step 1 exam was 227 with a standard deviation of 22. Assuming that the scores for 15,000 people follow a normal distribution, approximately how many students scored above the mean but below 250?
- A. 5,100 (Correct Answer)
- B. 4,500
- C. 6,000
- D. 3,750
- E. 6,750
Reporting in medical literature Explanation: ***5,100***
- To solve this, first calculate the **z-score** for 250: (250 - 227) / 22 = 1.045.
- Using a **z-table**, the area under the curve from the mean (z=0) to z=1.045 is approximately 0.353. Multiplying this by 15,000 students gives approximately **5,295 students**, which is closest to 5,100.
*4,500*
- This answer would imply a smaller proportion of students between the mean and 250 (around 30%), which is lower than the calculated z-score of 1.045 suggests.
- It does not accurately reflect the area under the **normal distribution curve** for the given range.
*6,000*
- This option would mean that approximately 40% of students scored in this range, which would correspond to a z-score much higher than 1.045 or a different standard deviation.
- This calculation overestimates the number of students within the specified range.
*3,750*
- This value represents 25% of the total students (15,000 * 0.25), indicating that only a quarter of the distribution lies in this range.
- This significantly underestimates the proportion of students scoring between the mean and 250 for the given standard deviation.
*6,750*
- This option reflects approximately 45% of the total student population (15,000 * 0.45), which would correspond to a much larger z-score or a different distribution.
- This value is an overestimation and does not align with the standard normal distribution probabilities for the given parameters.
Reporting in medical literature US Medical PG Question 9: A researcher has identified a chemical compound that she expects may contribute to the development of colorectal cancer. She designs an experiment where she exposes 70 mice to a diet containing this compound with another 50 mice in a control group that was fed a regular diet. After 9 months, the mice were evaluated for tumor development at necropsy. In total, 14 mice in the experimental group developed colorectal tumor burden, and 1 mouse in the control group developed tumors. Based on this experiment, what risk of colorectal cancer can be attributable to this chemical compound?
- A. 22.0%
- B. 2.0%
- C. 12.5%
- D. 18.0% (Correct Answer)
- E. 20.0%
Reporting in medical literature Explanation: ***18.0%***
- The **attributable risk (AR)** is calculated as the **incidence in the exposed group (Ie)** minus the **incidence in the unexposed group (Iu)**.
- In this case, **Ie = 14/70 = 0.20** and **Iu = 1/50 = 0.02**. Therefore, **AR = 0.20 - 0.02 = 0.18**, or **18.0%**.
*22.0%*
- This value might result from an incorrect calculation or misinterpretation of the attributable risk formula.
- It does not correctly represent the difference in risk between the exposed and unexposed groups.
*2.0%*
- This represents the **incidence of colorectal tumors in the control group (Iu)**, not the attributable risk.
- The attributable risk accounts for the excess risk specifically due to the exposure.
*12.5%*
- This value is not derived from the standard formula for attributable risk using the provided data.
- It might represent a misunderstanding of how to calculate risk difference from incidence rates.
*20.0%*
- This represents the **incidence of colorectal tumors in the experimental group (Ie)**, not the attributable risk.
- The attributable risk needs to subtract the background risk observed in the unexposed group.
Reporting in medical literature US Medical PG Question 10: A research fellow proposes a nested case-control study within an existing cohort examining antibiotic exposure and C. difficile infection. The mentor suggests this design wastes the cohort structure and that relative risk should be calculated instead. The fellow argues that odds ratios from nested case-control studies approximate relative risk while being more efficient. Evaluate the validity of each position and synthesize the optimal approach.
- A. Calculate RR from full cohort since all data are available and RR is more interpretable
- B. Use nested case-control only if computational resources are limited, otherwise use full cohort
- C. Use nested case-control with OR since it's mathematically equivalent to cohort RR with proper sampling (Correct Answer)
- D. Perform both analyses and compare results to validate the nested case-control approach
- E. Calculate hazard ratios using Cox regression as a compromise between efficiency and accuracy
Reporting in medical literature Explanation: ***Use nested case-control with OR since it's mathematically equivalent to cohort RR with proper sampling***
- In a **nested case-control study** using **incidence density sampling** (risk-set sampling), the **Odds Ratio (OR)** provides an unbiased estimate of the **Rate Ratio** or **Relative Risk (RR)** without requiring the rare disease assumption.
- This design is highly efficient as it preserves the **temporal sequence** of the cohort while significantly reducing the need to process exposure data for the entire **at-risk population**.
*Calculate RR from full cohort since all data are available and RR is more interpretable*
- While **Relative Risk** is intuitive, calculating it requires data for the **entire denominator**, which may be prohibitively expensive or time-consuming if additional exposure processing (e.g., biomarker testing) is needed.
- The mentor's insistence ignores the **efficiency gains** of the nested design, which provides the same statistical inference with a fraction of the data processing.
*Perform both analyses and compare results to validate the nested case-control approach*
- Performing both analyses is redundant and contradicts the primary goal of using a **nested case-control** design, which is to **save resources** by not analyzing the full cohort.
- Validation is unnecessary because the **mathematical validity** of the nested case-control method is already well-established in epidemiological theory.
*Use nested case-control only if computational resources are limited, otherwise use full cohort*
- The primary limitation addressed by nested designs is usually **resource-intensive exposure assessment** (e.g., expensive lab assays) rather than mere **computational power**.
- Even if resources are available, the nested approach is often preferred in large cohorts to maintain a manageable **sub-sample** while achieving nearly identical statistical power.
*Calculate hazard ratios using Cox regression as a compromise between efficiency and accuracy*
- **Cox regression** is typically performed on the **full cohort** data, whereas the fellow is specifically proposing a sampling method to reduce the data set size.
- While a **Hazard Ratio** is a valid measure of effect, it does not solve the resource issue unless used in conjunction with a **case-cohort** or nested design, which leads back to the fellow's original point.
More Reporting in medical literature US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.