Interpretation differences US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Interpretation differences. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Interpretation differences US Medical PG Question 1: You are conducting a study comparing the efficacy of two different statin medications. Two groups are placed on different statin medications, statin A and statin B. Baseline LDL levels are drawn for each group and are subsequently measured every 3 months for 1 year. Average baseline LDL levels for each group were identical. The group receiving statin A exhibited an 11 mg/dL greater reduction in LDL in comparison to the statin B group. Your statistical analysis reports a p-value of 0.052. Which of the following best describes the meaning of this p-value?
- A. There is a 95% chance that the difference in reduction of LDL observed reflects a real difference between the two groups
- B. Though A is more effective than B, there is a 5% chance the difference in reduction of LDL between the two groups is due to chance
- C. If 100 permutations of this experiment were conducted, 5 of them would show similar results to those described above
- D. This is a statistically significant result
- E. There is a 5.2% chance of observing a difference in reduction of LDL of 11 mg/dL or greater even if the two medications have identical effects (Correct Answer)
Interpretation differences Explanation: **There is a 5.2% chance of observing a difference in reduction of LDL of 11 mg/dL or greater even if the two medications have identical effects**
- The **p-value** represents the probability of observing results as extreme as, or more extreme than, the observed data, assuming the **null hypothesis** is true (i.e., there is no true difference between the groups).
- A p-value of 0.052 means there's approximately a **5.2% chance** that the observed 11 mg/dL difference (or a more substantial difference) occurred due to **random variation**, even if both statins were equally effective.
*There is a 95% chance that the difference in reduction of LDL observed reflects a real difference between the two groups*
- This statement is an incorrect interpretation of the p-value; it confuses the p-value with the **probability that the alternative hypothesis is true**.
- A p-value does not directly tell us the probability that the observed difference is "real" or due to the intervention being studied.
*Though A is more effective than B, there is a 5% chance the difference in reduction of LDL between the two groups is due to chance*
- This statement implies that Statin A is more effective, which cannot be concluded with a p-value of 0.052 if the significance level (alpha) was set at 0.05.
- While it's true there's a chance the difference is due to chance, claiming A is "more effective" based on this p-value before statistical significance is usually declared is misleading.
*If 100 permutations of this experiment were conducted, 5 of them would show similar results to those described above*
- This is an incorrect interpretation. The p-value does not predict the outcome of repeated experiments in this manner.
- It refers to the **probability under the null hypothesis in a single experiment**, not the frequency of results across multiple hypothetical repetitions.
*This is a statistically significant result*
- A p-value of 0.052 is generally considered **not statistically significant** if the conventional alpha level (significance level) is set at 0.05 (or 5%).
- For a result to be statistically significant at alpha = 0.05, the p-value must be **less than 0.05**.
Interpretation differences US Medical PG Question 2: A medical research study is evaluating an investigational novel drug (medication 1) as compared with standard therapy (medication 2) in patients presenting to the emergency department with myocardial infarction (MI). The study enrolled a total of 3,000 subjects, 1,500 in each study arm. Follow-up was conducted at 45 days post-MI. The following are the results of the trial:
Endpoints Medication 1 Medication 2 P-Value
Primary: death from cardiac causes 134 210 0.03
Secondary: hyperkalemia 57 70 0.4
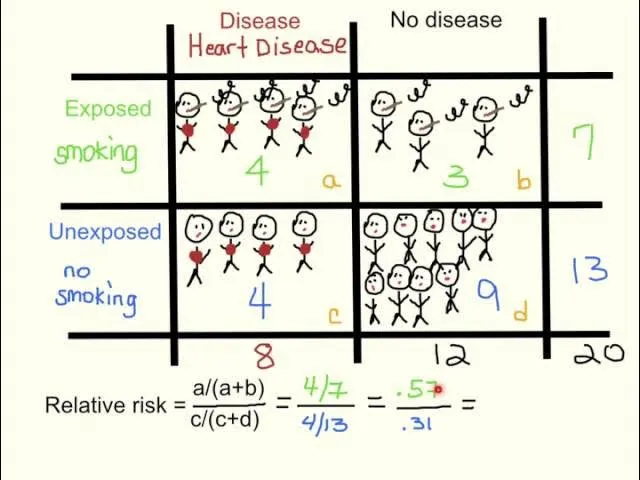
What is the relative risk of death from a cardiac cause, expressed as a percentage? (Round to the nearest whole number.)
- A. 64% (Correct Answer)
- B. 42%
- C. 72%
- D. 36%
- E. 57%
Interpretation differences Explanation: ***64%***
- The **relative risk (RR)** is calculated as the event rate in the exposed group divided by the event rate in the unexposed (control) group.
- For cardiac death, the event rate for Medication 1 is 134/1500 = 0.0893, and for Medication 2 is 210/1500 = 0.14. Therefore, RR = 0.0893 / 0.14 = 0.6378.
- Expressing as a percentage: 0.6378 × 100 = 63.78%, which rounds to **64%**.
- This indicates that Medication 1 has 64% of the risk of cardiac death compared to Medication 2, representing a **36% relative risk reduction**.
*42%*
- This option is incorrect as it does not reflect the accurate calculation of **relative risk** using the provided event rates.
- A calculation error or conceptual misunderstanding of the relative risk formula would lead to this value.
*72%*
- This percentage is higher than the calculated relative risk, suggesting an incorrect application of the formula or a misinterpretation of the event rates.
- It does not represent the ratio of risk between the two medication groups for cardiac death.
*36%*
- This value represents the **relative risk reduction** (100% - 64% = 36%), not the relative risk itself.
- This is a common error where students confuse relative risk with relative risk reduction.
*57%*
- While closer to the correct answer, this value is not the precise result when rounding to the nearest whole number.
- Small calculation discrepancies or rounding at intermediate steps could lead to this slightly different percentage.
Interpretation differences US Medical PG Question 3: A 6-month-old male presents for a routine visit to his pediatrician. Two months ago, the patient was seen for tachypnea and wheezing, and diagnosed with severe respiratory syncytial virus (RSV) bronchiolitis. After admission to the hospital and supportive care, the patient recovered and currently is not experiencing any trouble breathing. Regarding the possibility of future reactive airway disease, which of the following statements is most accurate?
- A. “There is no clear relationship between RSV and the development of asthma.”
- B. “Your child has a greater than 20% chance of developing asthma” (Correct Answer)
- C. “Your child’s risk of asthma is less than the general population.”
- D. “Your child has a less than 5% chance of developing asthma”
- E. “Your child’s risk of asthma is the same as the general population.”
Interpretation differences Explanation: ***“Your child has a greater than 20% chance of developing asthma”***
- Severe **RSV bronchiolitis** in infancy is a significant risk factor for the development of **recurrent wheezing** and **childhood asthma**.
- Studies estimate that a substantial proportion, often greater than 20%, of infants with severe RSV bronchiolitis will go on to develop **asthma** later in childhood.
*“There is no clear relationship between RSV and the development of asthma.”*
- This statement is incorrect as there is a **well-established link** between severe RSV infection in early life and an increased risk of developing **asthma**.
- Numerous epidemiological and longitudinal studies have documented this association.
*“Your child’s risk of asthma is less than the general population.”*
- This is incorrect, as severe RSV infection **increases** the risk of asthma, not decreases it.
- Children with a history of severe RSV have a **higher incidence** of asthma compared to the general pediatric population.
*“Your child has a less than 5% chance of developing asthma”*
- This percentage is **too low** given the known association between severe RSV bronchiolitis and subsequent asthma.
- The actual risk is considerably higher, typically falling into the range of 20-50% for those with severe RSV.
*“Your child’s risk of asthma is the same as the general population.”*
- This statement is inaccurate because severe RSV infection in infancy is a recognized independent **risk factor** for **asthma development**.
- Therefore, the child's risk is elevated above that of the general population.
Interpretation differences US Medical PG Question 4: A physician attempts to study cirrhosis in his state. Using a registry of admitted patients over the last 10 years at the local hospital, he isolates all patients who have been diagnosed with cirrhosis. Subsequently, he contacts this group of patients, asking them to complete a survey assessing their prior exposure to alcohol use, intravenous drug abuse, blood transfusions, personal history of cancer, and other medical comorbidities. An identical survey is given to an equal number of patients in the registry who do not carry a prior diagnosis of cirrhosis. Which of the following is the study design utilized by this physician?
- A. Randomized controlled trial
- B. Case-control study (Correct Answer)
- C. Cross-sectional study
- D. Cohort study
- E. Meta-analysis
Interpretation differences Explanation: ***Case-control study***
- This study design **identifies subjects based on their outcome (cases with cirrhosis, controls without cirrhosis)** and then retrospectively investigates their past exposures.
- The physician selected patients with cirrhosis (cases) and patients without cirrhosis (controls), then assessed their prior exposures to risk factors like alcohol use and intravenous drug abuse.
*Randomized controlled trial*
- This design involves randomly assigning participants to an **intervention group** or a **control group** to assess the effect of an intervention.
- There is no intervention being tested or randomization occurring in this study; it is observational.
*Cross-sectional study*
- A cross-sectional study measures the **prevalence of disease and exposure at a single point in time** in a defined population.
- This study collects retrospective exposure data and compares two distinct groups (cases and controls), rather than assessing prevalence at one time point.
*Cohort study*
- A cohort study **follows a group of individuals over time** to see if their exposure to a risk factor is associated with the development of a disease.
- This study starts with the outcome (cirrhosis) and looks backward at exposures, which is the opposite direction of a cohort study.
*Meta-analysis*
- A meta-analysis is a statistical method that **combines the results of multiple independent studies** to produce a single, more powerful estimate of treatment effect or association.
- This is an original research study collecting new data, not a systematic review or synthesis of existing studies.
Interpretation differences US Medical PG Question 5: A survey was conducted in a US midwestern town in an effort to assess maternal mortality over the past year. The data from the survey are given in the table below:
Women of childbearing age 250,000
Maternal deaths 2,500
Number of live births 100, 000
Number of deaths of women of childbearing age 7,500
Maternal death is defined as the death of a woman while pregnant or within 42 days of termination of pregnancy from any cause related to or aggravated by, the pregnancy. Which of the following is the maternal mortality rate in this midwestern town?
- A. 1,000 per 100,000 live births
- B. 33 per 100,000 live births
- C. 3,000 per 100,000 live births
- D. 33,300 per 100,000 live births
- E. 2,500 per 100,000 live births (Correct Answer)
Interpretation differences Explanation: ***2,500 per 100,000 live births***
- The maternal mortality rate is calculated as the number of **maternal deaths** per 100,000 **live births**. The given data directly provide these values.
- Calculation: (2,500 maternal deaths / 100,000 live births) × 100,000 = **2,500 per 100,000 live births**.
*1,000 per 100,000 live births*
- This value is incorrect as it does not align with the provided numbers for maternal deaths and live births in the calculation.
- It might result from a miscalculation or using incorrect numerator/denominator values from the dataset.
*33 per 100,000 live births*
- This value is significantly lower than the correct rate and suggests a substantial error in calculation or an incorrect understanding of how the maternal mortality rate is derived.
- It could potentially result from dividing the number of live births by maternal deaths, which is the inverse of the correct formula.
*3,000 per 100,000 live births*
- This option is close to the correct answer but slightly higher, indicating a possible calculation error, for instance, including non-maternal deaths or other causes of deaths in the numerator.
- The definition of maternal death is specific to pregnancy-related or aggravated causes, so extraneous deaths would inflate the rate.
*33,300 per 100,000 live births*
- This figure results from incorrectly calculating the proportion of maternal deaths among all deaths of women of childbearing age: (2,500 / 7,500) × 100,000 = 33,333.
- This is a conceptual error as the maternal mortality rate should use live births as the denominator, not total deaths of women of childbearing age.
Interpretation differences US Medical PG Question 6: In 2013 the national mean score on the USMLE Step 1 exam was 227 with a standard deviation of 22. Assuming that the scores for 15,000 people follow a normal distribution, approximately how many students scored above the mean but below 250?
- A. 5,100 (Correct Answer)
- B. 4,500
- C. 6,000
- D. 3,750
- E. 6,750
Interpretation differences Explanation: ***5,100***
- To solve this, first calculate the **z-score** for 250: (250 - 227) / 22 = 1.045.
- Using a **z-table**, the area under the curve from the mean (z=0) to z=1.045 is approximately 0.353. Multiplying this by 15,000 students gives approximately **5,295 students**, which is closest to 5,100.
*4,500*
- This answer would imply a smaller proportion of students between the mean and 250 (around 30%), which is lower than the calculated z-score of 1.045 suggests.
- It does not accurately reflect the area under the **normal distribution curve** for the given range.
*6,000*
- This option would mean that approximately 40% of students scored in this range, which would correspond to a z-score much higher than 1.045 or a different standard deviation.
- This calculation overestimates the number of students within the specified range.
*3,750*
- This value represents 25% of the total students (15,000 * 0.25), indicating that only a quarter of the distribution lies in this range.
- This significantly underestimates the proportion of students scoring between the mean and 250 for the given standard deviation.
*6,750*
- This option reflects approximately 45% of the total student population (15,000 * 0.45), which would correspond to a much larger z-score or a different distribution.
- This value is an overestimation and does not align with the standard normal distribution probabilities for the given parameters.
Interpretation differences US Medical PG Question 7: You are interested in studying the etiology of heart failure reduced ejection fraction (HFrEF) and attempt to construct an appropriate design study. Specifically, you wish to look for potential causality between dietary glucose consumption and HFrEF. Which of the following study designs would allow you to assess for and determine this causality?
- A. Cross-sectional study
- B. Case series
- C. Cohort study (Correct Answer)
- D. Case-control study
- E. Randomized controlled trial
Interpretation differences Explanation: ***Cohort study***
- A **cohort study** observes a group of individuals over time to identify risk factors and outcomes, allowing for the assessment of **temporal relationships** between exposure (dietary glucose) and outcome (HFrEF).
- This design is suitable for establishing a potential **causal link** as it tracks participants from exposure to outcome, enabling the calculation of incidence rates and relative risks.
*Cross-sectional study*
- A **cross-sectional study** measures exposure and outcome simultaneously at a single point in time, making it impossible to determine the **temporal sequence** of events.
- This design can only identify **associations** or correlations, not causation, as it cannot establish whether high glucose consumption preceded HFrEF.
*Case series*
- A **case series** describes characteristics of a group of patients with a particular disease or exposure, often to highlight unusual clinical features, but it lacks a **comparison group**.
- It cannot assess causality because it does not provide information on the frequency of exposure in healthy individuals or the incidence of the disease in unexposed individuals.
*Case-control study*
- A **case-control study** compares individuals with the outcome (cases) to those without the outcome (controls) to determine past exposures, which makes it prone to **recall bias**.
- While it can suggest associations, it cannot definitively establish a temporal relationship or causation as the outcome is already known when exposure is assessed.
*Randomized controlled trial*
- A **randomized controlled trial (RCT)** is the gold standard for establishing causation by randomly assigning participants to an intervention or control group, but it may not be ethical or feasible for studying long-term dietary exposures and chronic diseases like HFrEF due to the long follow-up period and complexity of diet.
- While ideal for causality, directly controlling and randomizing dietary glucose intake over decades to observe HFrEF development might be practically challenging or unethical.
Interpretation differences US Medical PG Question 8: A research fellow proposes a nested case-control study within an existing cohort examining antibiotic exposure and C. difficile infection. The mentor suggests this design wastes the cohort structure and that relative risk should be calculated instead. The fellow argues that odds ratios from nested case-control studies approximate relative risk while being more efficient. Evaluate the validity of each position and synthesize the optimal approach.
- A. Calculate RR from full cohort since all data are available and RR is more interpretable
- B. Use nested case-control only if computational resources are limited, otherwise use full cohort
- C. Use nested case-control with OR since it's mathematically equivalent to cohort RR with proper sampling (Correct Answer)
- D. Perform both analyses and compare results to validate the nested case-control approach
- E. Calculate hazard ratios using Cox regression as a compromise between efficiency and accuracy
Interpretation differences Explanation: ***Use nested case-control with OR since it's mathematically equivalent to cohort RR with proper sampling***
- In a **nested case-control study** using **incidence density sampling** (risk-set sampling), the **Odds Ratio (OR)** provides an unbiased estimate of the **Rate Ratio** or **Relative Risk (RR)** without requiring the rare disease assumption.
- This design is highly efficient as it preserves the **temporal sequence** of the cohort while significantly reducing the need to process exposure data for the entire **at-risk population**.
*Calculate RR from full cohort since all data are available and RR is more interpretable*
- While **Relative Risk** is intuitive, calculating it requires data for the **entire denominator**, which may be prohibitively expensive or time-consuming if additional exposure processing (e.g., biomarker testing) is needed.
- The mentor's insistence ignores the **efficiency gains** of the nested design, which provides the same statistical inference with a fraction of the data processing.
*Perform both analyses and compare results to validate the nested case-control approach*
- Performing both analyses is redundant and contradicts the primary goal of using a **nested case-control** design, which is to **save resources** by not analyzing the full cohort.
- Validation is unnecessary because the **mathematical validity** of the nested case-control method is already well-established in epidemiological theory.
*Use nested case-control only if computational resources are limited, otherwise use full cohort*
- The primary limitation addressed by nested designs is usually **resource-intensive exposure assessment** (e.g., expensive lab assays) rather than mere **computational power**.
- Even if resources are available, the nested approach is often preferred in large cohorts to maintain a manageable **sub-sample** while achieving nearly identical statistical power.
*Calculate hazard ratios using Cox regression as a compromise between efficiency and accuracy*
- **Cox regression** is typically performed on the **full cohort** data, whereas the fellow is specifically proposing a sampling method to reduce the data set size.
- While a **Hazard Ratio** is a valid measure of effect, it does not solve the resource issue unless used in conjunction with a **case-cohort** or nested design, which leads back to the fellow's original point.
Interpretation differences US Medical PG Question 9: Two studies examine statin therapy and stroke prevention. Study A (cohort, n=10,000) reports RR=0.75. Study B (case-control, n=2,000) reports OR=0.68. The absolute stroke rate in the general population is 2% over 5 years. Analyze these findings to determine which study provides more accurate information for clinical decision-making and why.
- A. Study B because case-control designs eliminate confounding
- B. Study B because odds ratios are more generalizable across populations
- C. Study A because relative risk is always more accurate than odds ratio
- D. Study A because the cohort design allows calculation of absolute risk reduction (Correct Answer)
- E. Both are equally valid since stroke is a rare outcome making OR approximate RR
Interpretation differences Explanation: ***Study A because the cohort design allows calculation of absolute risk reduction***
- **Study A (Cohort)** is superior for clinical decision-making because it directly measures **incidence**, enabling the calculation of **Absolute Risk Reduction (ARR)** and **Number Needed to Treat (NNT)**.
- **Cohort studies** establish a clear **temporal relationship** between exposure and outcome, providing stronger evidence for causality compared to retrospective designs.
*Study A because relative risk is always more accurate than odds ratio*
- **Relative Risk (RR)** is not inherently more "accurate," but it is mathematically more appropriate for describing risk in populations where **incidence** is known.
- The term accuracy refers to the lack of **bias** and **random error**, whereas RR and OR are simply different measures of association depending on study design.
*Study B because case-control designs eliminate confounding*
- **Case-control designs** are actually more prone to **selection and recall bias** and do not inherently eliminate **confounding** better than cohort studies.
- Confounding is typically controlled through **matching**, **stratification**, or **multivariate analysis** regardless of the study design used.
*Study B because odds ratios are more generalizable across populations*
- **Odds Ratios (OR)** are not more generalizable; they are frequently used in case-control studies because **incidence** cannot be directly calculated in those samples.
- Generalizability depends on the **representativeness** of the study sample to the target population, not on the mathematical measure (OR vs RR) used.
*Both are equally valid since stroke is a rare outcome making OR approximate RR*
- While the **Rare Disease Assumption** states that OR approximates RR when outcome prevalence is low (<10%), their clinical utility still differs.
- Even if the values are similar, the **Cohort study (Study A)** remains more robust for clinical decisions as it provides the **denominator** needed to calculate absolute benefits.
Interpretation differences US Medical PG Question 10: A genetic epidemiology study uses a case-control design to examine BRCA1 mutations and breast cancer risk, reporting an odds ratio of 15.0 (95% CI: 8.2-27.4). A patient with a BRCA1 mutation asks what this means for her actual risk of developing breast cancer. Evaluate how to appropriately counsel this patient regarding the study findings.
- A. The confidence interval suggests her risk is between 8-27 times higher
- B. The odds ratio cannot be directly interpreted as risk; population incidence data are needed (Correct Answer)
- C. Convert OR to RR using the formula: RR = OR/(1 + P0(OR-1)) where P0 is baseline risk
- D. Her risk is 15 times higher than women without the mutation
- E. She has a 15% absolute risk of developing breast cancer
Interpretation differences Explanation: ***The odds ratio cannot be directly interpreted as risk; population incidence data are needed***
- In a **case-control study**, the **Odds Ratio (OR)** represents the odds of exposure among cases versus controls, not the **probability** or risk of developing the disease.
- To determine actual **individual risk**, information on the **baseline population incidence** or absolute risk is required, which this study design does not provide.
*Her risk is 15 times higher than women without the mutation*
- This statement incorrectly equates OR with **Relative Risk (RR)**; while they are similar for rare diseases, they are distinct mathematical concepts.
- An OR of 15.0 means the **odds** are 15 times higher, but the **risk** (probability) might be lower than 15-fold depending on the prevalence.
*She has a 15% absolute risk of developing breast cancer*
- The OR is a **ratio of odds**, not a **percentage of absolute risk**; a value of 15.0 describes the strength of association, not a 15/100 probability.
- Absolute risk can only be calculated from **cohort studies** where the incidence of the disease is measured over time.
*Convert OR to RR using the formula: RR = OR/(1 + P0(OR-1)) where P0 is baseline risk*
- While this formula is mathematically used to convert OR to RR, it requires knowledge of the **baseline risk (P0)** in the unexposed population, which is not provided in a case-control study.
- Providing this formula to a patient is clinically inappropriate for **counseling** as it does not translate directly to her personal clinical outcome.
*The confidence interval suggests her risk is between 8-27 times higher*
- The **95% Confidence Interval (CI)** describes the precision and statistical significance of the **odds ratio**, not the range of individual risk.
- Using the CI to estimate **magnitude of risk** for a patient persists the same error of treating the OR as an equivalent to Relative Risk.
More Interpretation differences US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.