Common misinterpretations US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Common misinterpretations. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Common misinterpretations US Medical PG Question 1: A study is funded by the tobacco industry to examine the association between smoking and lung cancer. They design a study with a prospective cohort of 1,000 smokers between the ages of 20-30. The length of the study is five years. After the study period ends, they conclude that there is no relationship between smoking and lung cancer. Which of the following study features is the most likely reason for the failure of the study to note an association between tobacco use and cancer?
- A. Late-look bias
- B. Latency period (Correct Answer)
- C. Confounding
- D. Effect modification
- E. Pygmalion effect
Common misinterpretations Explanation: ***Latency period***
- **Lung cancer** typically has a **long latency period**, often **20-30+ years**, between initial exposure to tobacco carcinogens and the development of clinically detectable disease.
- A **five-year study duration** in young smokers (ages 20-30) is **far too short** to observe the development of lung cancer, which explains the false negative finding.
- This represents a **fundamental flaw in study design** rather than a bias—the biological timeline of disease development was not adequately considered.
*Late-look bias*
- **Late-look bias** occurs when a study enrolls participants who have already survived the early high-risk period of a disease, leading to **underestimation of true mortality or incidence**.
- Also called **survival bias**, it involves studying a population that has already been "selected" by survival.
- This is not applicable here, as the study simply ended before sufficient time elapsed for disease to develop.
*Confounding*
- **Confounding** occurs when a third variable is associated with both the exposure and outcome, distorting the apparent relationship between them.
- While confounding can affect study results, it would not completely eliminate the detection of a strong, well-established association like smoking and lung cancer in a properly conducted prospective cohort study.
- The issue here is temporal (insufficient follow-up time), not the presence of an unmeasured confounder.
*Effect modification*
- **Effect modification** (also called interaction) occurs when the magnitude of an association between exposure and outcome differs across levels of a third variable.
- This represents a **true biological phenomenon**, not a study design flaw or bias.
- It would not explain the complete failure to detect any association.
*Pygmalion effect*
- The **Pygmalion effect** (observer-expectancy effect) refers to a psychological phenomenon where higher expectations lead to improved performance in the observed subjects.
- This concept is relevant to **behavioral and educational research**, not to objective epidemiological studies of disease incidence.
- It has no relevance to the biological relationship between carcinogen exposure and cancer development.
Common misinterpretations US Medical PG Question 2: Group of 100 medical students took an end of the year exam. The mean score on the exam was 70%, with a standard deviation of 25%. The professor states that a student's score must be within the 95% confidence interval of the mean to pass the exam. Which of the following is the minimum score a student can have to pass the exam?
- A. 45%
- B. 63.75%
- C. 67.5%
- D. 20%
- E. 65% (Correct Answer)
Common misinterpretations Explanation: ***65%***
- To find the **95% confidence interval (CI) of the mean**, we use the formula: Mean ± (Z-score × Standard Error). For a 95% CI, the Z-score is approximately **1.96**.
- The **Standard Error (SE)** is calculated as SD/√n, where n is the sample size (100 students). So, SE = 25%/√100 = 25%/10 = **2.5%**.
- The 95% CI is 70% ± (1.96 × 2.5%) = 70% ± 4.9%. The lower bound is 70% - 4.9% = **65.1%**, which rounds to **65%** as the minimum passing score.
*45%*
- This value is significantly lower than the calculated lower bound of the 95% confidence interval (approximately 65.1%).
- It would represent a score far outside the defined passing range.
*63.75%*
- This value falls below the calculated lower bound of the 95% confidence interval (approximately 65.1%).
- While close, this score would not meet the professor's criterion for passing.
*67.5%*
- This value is within the 95% confidence interval (65.1% to 74.9%) but is **not the minimum score**.
- Lower scores within the interval would still qualify as passing.
*20%*
- This score is extremely low and falls significantly outside the 95% confidence interval for a mean of 70%.
- It would indicate performance far below the defined passing threshold.
Common misinterpretations US Medical PG Question 3: A surgeon is interested in studying how different surgical techniques impact the healing of tendon injuries. In particular, he will compare 3 different types of suture repairs biomechanically in order to determine the maximum load before failure of the tendon 2 weeks after repair. He collects data on maximum load for 90 different repaired tendons from an animal model. Thirty tendons were repaired using each of the different suture techniques. Which of the following statistical measures is most appropriate for analyzing the results of this study?
- A. Chi-squared
- B. Wilcoxon rank sum
- C. Pearson r coefficient
- D. Student t-test
- E. ANOVA (Correct Answer)
Common misinterpretations Explanation: ***ANOVA***
- **ANOVA (Analysis of Variance)** is appropriate here because it compares the means of **three or more independent groups** (the three different suture techniques) on a continuous dependent variable (maximum load before failure).
- The study has three distinct repair techniques, each with 30 tendons, making ANOVA suitable for determining if there are statistically significant differences among their mean failure loads.
*Chi-squared*
- The **Chi-squared test** is used for analyzing **categorical data** (frequencies or proportions) to determine if there is an association between two nominal variables.
- This study involves quantitative measurement (maximum load), not categorical data, making Chi-squared inappropriate.
*Wilcoxon rank sum*
- The **Wilcoxon rank sum test** (also known as Mann-Whitney U test) is a **non-parametric test** used to compare two independent groups when the data is not normally distributed or is ordinal.
- While the study has independent groups, it involves three groups, and the dependent variable is continuous, making ANOVA a more powerful and appropriate choice assuming normal distribution.
*Pearson r coefficient*
- The **Pearson r coefficient** measures the **strength and direction of a linear relationship between two continuous variables**.
- This study aims to compare means across different groups, not to determine the correlation between two continuous variables.
*Student t-test*
- The **Student t-test** is used to compare the means of **exactly two groups** (either independent or paired) on a continuous dependent variable.
- This study involves comparing three different suture techniques, not just two, making the t-test unsuitable.
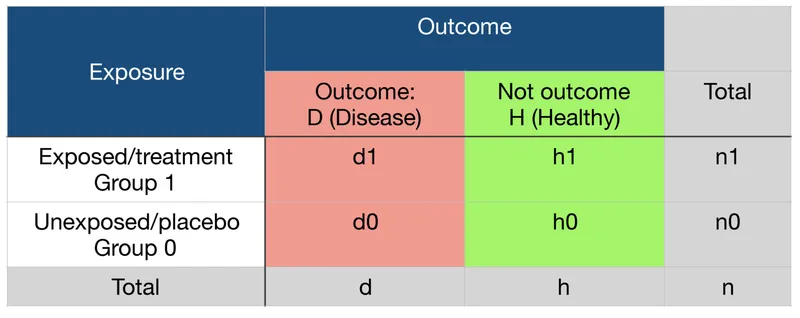
Common misinterpretations US Medical PG Question 4: A medical research study is evaluating an investigational novel drug (medication 1) as compared with standard therapy (medication 2) in patients presenting to the emergency department with myocardial infarction (MI). The study enrolled a total of 3,000 subjects, 1,500 in each study arm. Follow-up was conducted at 45 days post-MI. The following are the results of the trial:
Endpoints Medication 1 Medication 2 P-Value
Primary: death from cardiac causes 134 210 0.03
Secondary: hyperkalemia 57 70 0.4
What is the relative risk of death from a cardiac cause, expressed as a percentage? (Round to the nearest whole number.)
- A. 64% (Correct Answer)
- B. 42%
- C. 72%
- D. 36%
- E. 57%
Common misinterpretations Explanation: ***64%***
- The **relative risk (RR)** is calculated as the event rate in the exposed group divided by the event rate in the unexposed (control) group.
- For cardiac death, the event rate for Medication 1 is 134/1500 = 0.0893, and for Medication 2 is 210/1500 = 0.14. Therefore, RR = 0.0893 / 0.14 = 0.6378.
- Expressing as a percentage: 0.6378 × 100 = 63.78%, which rounds to **64%**.
- This indicates that Medication 1 has 64% of the risk of cardiac death compared to Medication 2, representing a **36% relative risk reduction**.
*42%*
- This option is incorrect as it does not reflect the accurate calculation of **relative risk** using the provided event rates.
- A calculation error or conceptual misunderstanding of the relative risk formula would lead to this value.
*72%*
- This percentage is higher than the calculated relative risk, suggesting an incorrect application of the formula or a misinterpretation of the event rates.
- It does not represent the ratio of risk between the two medication groups for cardiac death.
*36%*
- This value represents the **relative risk reduction** (100% - 64% = 36%), not the relative risk itself.
- This is a common error where students confuse relative risk with relative risk reduction.
*57%*
- While closer to the correct answer, this value is not the precise result when rounding to the nearest whole number.
- Small calculation discrepancies or rounding at intermediate steps could lead to this slightly different percentage.
Common misinterpretations US Medical PG Question 5: You are reading through a recent article that reports significant decreases in all-cause mortality for patients with malignant melanoma following treatment with a novel biological infusion. Which of the following choices refers to the probability that a study will find a statistically significant difference when one truly does exist?
- A. Type II error
- B. Type I error
- C. Confidence interval
- D. p-value
- E. Power (Correct Answer)
Common misinterpretations Explanation: ***Power***
- **Power** is the probability that a study will correctly reject the null hypothesis when it is, in fact, false (i.e., will find a statistically significant difference when one truly exists).
- A study with high power minimizes the risk of a **Type II error** (failing to detect a real effect).
*Type II error*
- A **Type II error** (or **beta error**) occurs when a study fails to reject a false null hypothesis, meaning it concludes there is no significant difference when one actually exists.
- This is the **opposite** of what the question describes, which asks for the probability of *finding* a difference.
*Type I error*
- A **Type I error** (or **alpha error**) occurs when a study incorrectly rejects a true null hypothesis, concluding there is a significant difference when one does not actually exist.
- This relates to the **p-value** and the level of statistical significance (e.g., p < 0.05).
*Confidence interval*
- A **confidence interval** provides a range of values within which the true population parameter is likely to lie with a certain degree of confidence (e.g., 95%).
- It does not directly represent the probability of finding a statistically significant difference when one truly exists.
*p-value*
- The **p-value** is the probability of observing data as extreme as, or more extreme than, that obtained in the study, assuming the null hypothesis is true.
- It is used to determine statistical significance, but it is not the probability of detecting a true effect.
Common misinterpretations US Medical PG Question 6: Study X examined the relationship between coffee consumption and lung cancer. The authors of Study X retrospectively reviewed patients' reported coffee consumption and found that drinking greater than 6 cups of coffee per day was associated with an increased risk of developing lung cancer. However, Study X was criticized by the authors of Study Y. Study Y showed that increased coffee consumption was associated with smoking. What type of bias affected Study X, and what study design is geared to reduce the chance of that bias?
- A. Observer bias; double blind analysis
- B. Selection bias; randomization
- C. Lead time bias; placebo
- D. Measurement bias; blinding
- E. Confounding; randomization (Correct Answer)
Common misinterpretations Explanation: ***Confounding; randomization***
- Study Y suggests that **smoking** is a **confounding variable** because it is associated with both increased coffee consumption (exposure) and increased risk of lung cancer (outcome), distorting the apparent relationship between coffee and lung cancer.
- **Randomization** in experimental studies (such as randomized controlled trials) helps reduce confounding by ensuring that known and unknown confounding factors are evenly distributed among study groups.
- In observational studies where randomization is not possible, confounding can be addressed through **stratification**, **matching**, or **multivariable adjustment** during analysis.
*Observer bias; double blind analysis*
- **Observer bias** occurs when researchers' beliefs or expectations influence the study outcome, which is not the primary issue described here regarding the relationship between coffee, smoking, and lung cancer.
- **Double-blind analysis** is a method to mitigate observer bias by ensuring neither participants nor researchers know who is in the control or experimental groups.
*Selection bias; randomization*
- **Selection bias** happens when the study population is not representative of the target population, leading to inaccurate results, which is not directly indicated by the interaction between coffee and smoking.
- While **randomization** is used to reduce selection bias by creating comparable groups, the core problem identified in Study X is confounding, not flawed participant selection.
*Lead time bias; placebo*
- **Lead time bias** occurs in screening programs when early detection without improved outcomes makes survival appear longer, an issue unrelated to the described association between coffee, smoking, and lung cancer.
- A **placebo** is an inactive treatment used in clinical trials to control for psychological effects, and its relevance here is limited to treatment intervention studies.
*Measurement bias; blinding*
- **Measurement bias** arises from systematic errors in data collection, such as inaccurate patient reporting of coffee consumption, but the main criticism from Study Y points to a third variable (smoking) affecting the association, not just flawed measurement.
- **Blinding** helps reduce measurement bias by preventing participants or researchers from knowing group assignments, thus minimizing conscious or unconscious influences on data collection.
Common misinterpretations US Medical PG Question 7: You submit a paper to a prestigious journal about the effects of coffee consumption on mesothelioma risk. The first reviewer lauds your clinical and scientific acumen, but expresses concern that your study does not have adequate statistical power. Statistical power refers to which of the following?
- A. The probability of detecting an association when no association exists.
- B. The probability of not detecting an association when an association does exist.
- C. The probability of detecting an association when an association does exist. (Correct Answer)
- D. The first derivative of work.
- E. The square root of the variance.
Common misinterpretations Explanation: ***The probability of detecting an association when an association does exist.***
- **Statistical power** is defined as the probability that a study will correctly reject a false null hypothesis, meaning it will detect a true effect or association if one exists.
- A study with **adequate statistical power** is less likely to miss a real effect.
*The probability of detecting an association when no association exists.*
- This describes a **Type I error** or **false positive**, often represented by **alpha (α)**.
- It is the probability of incorrectly concluding an effect or association exists when, in reality, there is none.
*The probability of not detecting an association when an association does exist.*
- This refers to a **Type II error** or **false negative**, represented by **beta (β)**.
- **Statistical power** is calculated as **1 - β**, so this option describes the complement of power.
*The first derivative of work.*
- The first derivative of work with respect to time represents **power** in physics, which is the rate at which work is done.
- This option is a **distractor** from physics and is unrelated to statistical power in research.
*The square root of the variance.*
- The **square root of the variance** is the **standard deviation**, a measure of the dispersion or spread of data.
- This is a statistical concept but is not the definition of statistical power.
Common misinterpretations US Medical PG Question 8: During an evaluation of a new diagnostic imaging modality for detecting salivary gland tumors, 90 patients tested positive out of the 100 patients who tested positive with the gold standard test. A total of 80 individuals tested negative with the new test out of the 100 individuals who tested negative with the gold standard test. What is the positive likelihood ratio for this test?
- A. 80/90
- B. 90/100
- C. 90/20 (Correct Answer)
- D. 90/110
- E. 10/80
Common misinterpretations Explanation: ***90/20***
- The **positive likelihood ratio (LR+)** is calculated as **sensitivity / (1 - specificity)**. To calculate this, we first need to determine the values for true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN).
- Given that 90 out of 100 actual positive patients tested positive, **TP = 90** and **FN = 100 - 90 = 10**. Also, 80 out of 100 actual negative patients tested negative, so **TN = 80** and **FP = 100 - 80 = 20**.
- **Sensitivity** is the true positive rate (TP / (TP + FN)) = 90 / (90 + 10) = 90 / 100.
- **Specificity** is the true negative rate (TN / (TN + FP)) = 80 / (80 + 20) = 80 / 100.
- Therefore, LR+ = (90/100) / (1 - 80/100) = (90/100) / (20/100) = **90/20**.
*80/90*
- This option incorrectly represents the components for the likelihood ratio. It seems to misinterpret the **true negative** count and the **true positive** count.
- It does not follow the formula for LR+ which is **sensitivity / (1 - specificity)**.
*90/100*
- This value represents the **sensitivity** of the test, which is the proportion of true positives among all actual positives.
- It does not incorporate the **false positive rate** (1 - specificity) in the denominator required for the positive likelihood ratio.
*90/110*
- This option incorrectly combines different values, possibly by confusing the denominator for sensitivity or specificity calculations.
- It does not correspond to the formula for the **positive likelihood ratio**.
*10/80*
- This value seems to relate to the inverse of the **false negative rate** (10/100) or misrepresents the relationship between false negatives and true negatives.
- It is not correctly structured to represent the **positive likelihood ratio (LR+)**.
Common misinterpretations US Medical PG Question 9: In 2013 the national mean score on the USMLE Step 1 exam was 227 with a standard deviation of 22. Assuming that the scores for 15,000 people follow a normal distribution, approximately how many students scored above the mean but below 250?
- A. 5,100 (Correct Answer)
- B. 4,500
- C. 6,000
- D. 3,750
- E. 6,750
Common misinterpretations Explanation: ***5,100***
- To solve this, first calculate the **z-score** for 250: (250 - 227) / 22 = 1.045.
- Using a **z-table**, the area under the curve from the mean (z=0) to z=1.045 is approximately 0.353. Multiplying this by 15,000 students gives approximately **5,295 students**, which is closest to 5,100.
*4,500*
- This answer would imply a smaller proportion of students between the mean and 250 (around 30%), which is lower than the calculated z-score of 1.045 suggests.
- It does not accurately reflect the area under the **normal distribution curve** for the given range.
*6,000*
- This option would mean that approximately 40% of students scored in this range, which would correspond to a z-score much higher than 1.045 or a different standard deviation.
- This calculation overestimates the number of students within the specified range.
*3,750*
- This value represents 25% of the total students (15,000 * 0.25), indicating that only a quarter of the distribution lies in this range.
- This significantly underestimates the proportion of students scoring between the mean and 250 for the given standard deviation.
*6,750*
- This option reflects approximately 45% of the total student population (15,000 * 0.45), which would correspond to a much larger z-score or a different distribution.
- This value is an overestimation and does not align with the standard normal distribution probabilities for the given parameters.
Common misinterpretations US Medical PG Question 10: You are interested in studying the etiology of heart failure reduced ejection fraction (HFrEF) and attempt to construct an appropriate design study. Specifically, you wish to look for potential causality between dietary glucose consumption and HFrEF. Which of the following study designs would allow you to assess for and determine this causality?
- A. Cross-sectional study
- B. Case series
- C. Cohort study (Correct Answer)
- D. Case-control study
- E. Randomized controlled trial
Common misinterpretations Explanation: ***Cohort study***
- A **cohort study** observes a group of individuals over time to identify risk factors and outcomes, allowing for the assessment of **temporal relationships** between exposure (dietary glucose) and outcome (HFrEF).
- This design is suitable for establishing a potential **causal link** as it tracks participants from exposure to outcome, enabling the calculation of incidence rates and relative risks.
*Cross-sectional study*
- A **cross-sectional study** measures exposure and outcome simultaneously at a single point in time, making it impossible to determine the **temporal sequence** of events.
- This design can only identify **associations** or correlations, not causation, as it cannot establish whether high glucose consumption preceded HFrEF.
*Case series*
- A **case series** describes characteristics of a group of patients with a particular disease or exposure, often to highlight unusual clinical features, but it lacks a **comparison group**.
- It cannot assess causality because it does not provide information on the frequency of exposure in healthy individuals or the incidence of the disease in unexposed individuals.
*Case-control study*
- A **case-control study** compares individuals with the outcome (cases) to those without the outcome (controls) to determine past exposures, which makes it prone to **recall bias**.
- While it can suggest associations, it cannot definitively establish a temporal relationship or causation as the outcome is already known when exposure is assessed.
*Randomized controlled trial*
- A **randomized controlled trial (RCT)** is the gold standard for establishing causation by randomly assigning participants to an intervention or control group, but it may not be ethical or feasible for studying long-term dietary exposures and chronic diseases like HFrEF due to the long follow-up period and complexity of diet.
- While ideal for causality, directly controlling and randomizing dietary glucose intake over decades to observe HFrEF development might be practically challenging or unethical.
More Common misinterpretations US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.