Test characteristics fundamentals US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Test characteristics fundamentals. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Test characteristics fundamentals US Medical PG Question 1: A 31-year-old woman gives birth to a boy in the labor and delivery ward of the local hospital. The child is immediately assessed and found to be crying vigorously. He is pink in appearance with blue extremities that appear to be flexed. Inducing some discomfort shows that both his arms and legs move slightly but remain largely flexed throughout. His pulse is found to be 128 beats per minute. What is the most likely APGAR score for this newborn at this time?
- A. 8 (Correct Answer)
- B. 5
- C. 9
- D. 6
- E. 7
Test characteristics fundamentals Explanation: ***8***
- The assessment breaks down as: **Appearance** (pink body with blue extremities/acrocyanosis) = 1 point; **Pulse** (128 bpm, >100) = 2 points; **Grimace** (crying vigorously in response to discomfort) = 2 points; **Activity** (slight movement but remains largely flexed) = 1 point; **Respiration** (crying vigorously) = 2 points. Total = **8**.
- An APGAR score of 8-10 is considered **normal** and indicates a healthy newborn with only minor deductions (in this case, acrocyanosis which is common and benign).
*7*
- A score of 7 would require one fewer point, such as only 1 point for **Respiration** (weak cry or slow breathing) instead of 2 points.
- The infant's **vigorous crying** clearly merits 2 points for respiration, not 1, making a score of 7 incorrect.
*9*
- A score of 9 would require either fully pink appearance (2 points for Appearance) or active movement against resistance (2 points for Activity).
- The infant's **acrocyanosis** (blue extremities) limits Appearance to 1 point, and **limited activity** (largely flexed with only slight movement) prevents a score of 9.
*5*
- A score of 5 suggests moderate distress with significantly lower scores across multiple categories.
- The infant's strong pulse (2 points), vigorous crying (2 points each for Grimace and Respiration), and reasonable activity contradict an APGAR score of 5.
*6*
- A score of 6 would imply lower scores in at least two categories compared to the given findings.
- The infant's excellent cardiovascular (pulse 128 bpm = 2 points) and respiratory status (vigorous cry = 2 points) make a score of 6 too low.
Test characteristics fundamentals US Medical PG Question 2: An infectious disease investigator is evaluating the diagnostic accuracy of a new interferon-gamma-based assay for diagnosing tuberculosis in patients who have previously received a Bacillus Calmette-Guérin (BCG) vaccine. Consenting participants with a history of BCG vaccination received an interferon-gamma assay and were subsequently evaluated for tuberculosis by sputum culture. Results of the study are summarized in the table below.
Tuberculosis, confirmed by culture No tuberculosis Total
Positive interferon-gamma assay 90 6 96
Negative interferon-gamma assay 10 194 204
Total 100 200 300
Based on these results, what is the sensitivity of the interferon-gamma-based assay for the diagnosis of tuberculosis in this study?
- A. 90/96
- B. 100/300
- C. 194/200
- D. 90/100 (Correct Answer)
- E. 194/204
Test characteristics fundamentals Explanation: ***90/100***
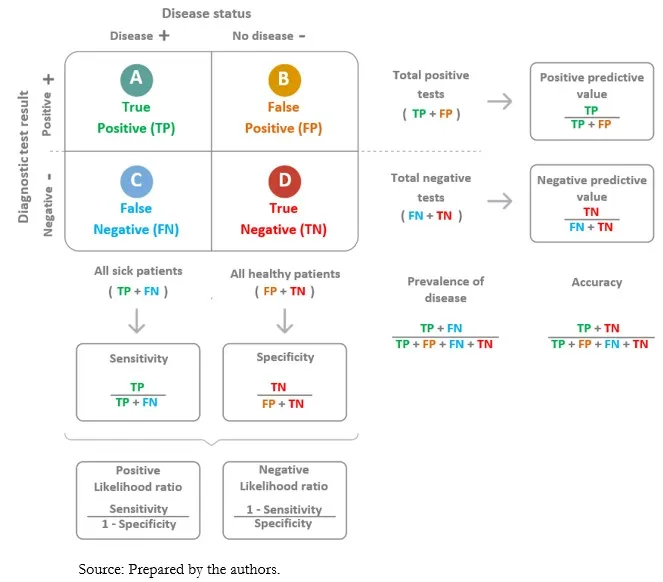
- **Sensitivity** measures the proportion of **true positive** cases that are correctly identified by the test.
- In this study, there are 90 true positive results (positive interferon-gamma assay in patients with confirmed tuberculosis) out of a total of 100 individuals with confirmed tuberculosis (90 + 10).
*90/96*
- This calculation represents the **positive predictive value** (90 true positives / 96 total positive tests).
- It answers the question: "If the test is positive, what is the likelihood that the patient actually has the disease?"
*100/300*
- This value represents the prevalence of tuberculosis in the study population (100 confirmed cases / 300 total participants).
- It does not reflect a measure of the test's diagnostic accuracy.
*194/200*
- This value represents the **specificity** of the test (194 true negatives / 200 total individuals without tuberculosis).
- Specificity measures the proportion of true negative cases that are correctly identified by the test.
*194/204*
- This calculation represents the **negative predictive value** (194 true negatives / 204 total negative tests).
- It answers the question: "If the test is negative, what is the likelihood that the patient does not have the disease?"
Test characteristics fundamentals US Medical PG Question 3: A home drug screening test kit is currently being developed. The cut-off level is initially set at 4 mg/uL, which is associated with a sensitivity of 92% and a specificity of 97%. How might the sensitivity and specificity of the test change if the cut-off level is changed to 2 mg/uL?
- A. Sensitivity = 92%, specificity = 97%
- B. Sensitivity = 95%, specificity = 98%
- C. Sensitivity = 100%, specificity = 97%
- D. Sensitivity = 90%, specificity = 99%
- E. Sensitivity = 97%, specificity = 96% (Correct Answer)
Test characteristics fundamentals Explanation: ***Sensitivity = 97%, specificity = 96%***
- Lowering the cut-off from 4 mg/uL to 2 mg/uL means that more individuals will be classified as **positive** (anyone with drug levels ≥2 mg/uL instead of ≥4 mg/uL). This change will **increase the sensitivity** (capturing more true positives, fewer false negatives) but **decrease the specificity** (more false positives among those without the condition).
- Therefore, sensitivity will increase (e.g., to 97%), and specificity will decrease (e.g., to 96%), reflecting the fundamental trade-off between these metrics.
*Sensitivity = 92%, specificity = 97%*
- This option reflects the **original values** at the 4 mg/uL cut-off and does not account for the change in the threshold.
- A change in the cut-off level will inherently alter the test's performance characteristics.
*Sensitivity = 95%, specificity = 98%*
- This option suggests an increase in **both sensitivity and specificity**, which is generally not possible by simply changing the cut-off level in the same direction.
- There is typically an **inverse relationship** between sensitivity and specificity when adjusting the cut-off threshold.
*Sensitivity = 100%, specificity = 97%*
- Reaching **100% sensitivity** while maintaining a high specificity is highly unlikely with a simple cut-off adjustment.
- While sensitivity would increase with a lower cut-off, achieving perfect sensitivity is unrealistic in clinical practice.
*Sensitivity = 90%, specificity = 99%*
- This option suggests a **decrease in sensitivity** and an **increase in specificity**.
- A lower cut-off would lead to more positive results, thus increasing sensitivity and reducing specificity, which contradicts the proposed values.
Test characteristics fundamentals US Medical PG Question 4: A 27-year-old man interested in pre-exposure therapy for HIV (PrEP) is being evaluated to qualify for a PrEP study. In order to qualify, patients must be HIV- and hepatitis B- and C-negative. Any other sexually transmitted infections require treatment prior to initiation of PrEP. The medical history is positive for a prior syphilis infection and bipolar affective disorder, for which he takes lithium. On his next visit, the liver and renal enzymes are within normal ranges. HIV and hepatitis B and C tests are negative. Which of the following about the HIV test is true?
- A. It is a quantitative test used for screening purposes.
- B. It is a qualitative test used for screening purposes. (Correct Answer)
- C. A secondary reagent is needed to interpret the results.
- D. A known antigen binds directly to the patient's serum.
- E. An unknown antigen binds to the known serum.
Test characteristics fundamentals Explanation: ***It is a qualitative test used for screening purposes.***
- **HIV screening tests** (e.g., 4th generation antibody/antigen combination assays) are typically **qualitative**, meaning they detect the presence or absence of HIV markers, not their exact amount.
- These tests are primarily used for broad **screening** of populations to identify potential cases of HIV infection.
*It is a quantitative test used for screening purposes.*
- **Quantitative tests** for HIV, such as viral load tests, measure the amount of virus in the blood and are typically used for monitoring disease progression or treatment effectiveness, not for initial screening.
- Screening tests are designed for high sensitivity to detect infection, even with low viral loads or early antibody responses, making a quantitative measurement less relevant for initial screening.
*A secondary reagent is needed to interpret the results.*
- While some complex immunoassays might involve multiple steps, modern **HIV screening tests** often use advanced technologies that directly yield results, making a separate secondary reagent for interpretation generally unnecessary.
- The results are typically indicated by a color change or a signal detected by an instrument, without requiring an additional interpretive reagent.
*A known antigen binds directly to the patient's serum.*
- **HIV antibody tests** detect **antibodies** produced by the patient's immune system in response to HIV infection.
- In such tests, **known HIV antigens** (from the test kit) bind to **HIV-specific antibodies present in the patient's serum**, not to serum components directly.
- This option is incorrect because it omits the critical role of antibodies as the target molecules being detected.
*An unknown antigen binds to the known serum.*
- This statement describes a different type of immunological assay where an unknown antigen is being identified using a known antibody, which is contrary to how **HIV screening tests** for infection are typically structured.
- **HIV screening tests** use known components (e.g., HIV antigens or antibodies) in the test kit to detect unknown components (e.g., HIV antibodies or viral antigens) in the patient's sample.
Test characteristics fundamentals US Medical PG Question 5: A medical research study is beginning to evaluate the positive predictive value of a novel blood test for non-Hodgkin’s lymphoma. The diagnostic arm contains 700 patients with NHL, of which 400 tested positive for the novel blood test. In the control arm, 700 age-matched control patients are enrolled and 0 are found positive for the novel test. What is the PPV of this test?
- A. 400 / (400 + 0) (Correct Answer)
- B. 700 / (700 + 300)
- C. 400 / (400 + 300)
- D. 700 / (700 + 0)
- E. 700 / (400 + 400)
Test characteristics fundamentals Explanation: ***400 / (400 + 0) = 1.0 or 100%***
- The **positive predictive value (PPV)** is calculated as **True Positives / (True Positives + False Positives)**.
- In this scenario, **True Positives (TP)** are the 400 patients with NHL who tested positive, and **False Positives (FP)** are 0, as no control patients tested positive.
- This gives a PPV of 400/400 = **1.0 or 100%**, indicating that all patients who tested positive actually had the disease.
*700 / (700 + 300)*
- This calculation does not align with the formula for PPV based on the given data.
- The denominator `(700+300)` suggests an incorrect combination of various patient groups.
*400 / (400 + 300)*
- The denominator `(400+300)` incorrectly includes 300, which is the number of **False Negatives** (patients with NHL who tested negative), not False Positives.
- PPV focuses on the proportion of true positives among all positive tests, not all diseased individuals.
*700 / (700 + 0)*
- This calculation incorrectly uses the total number of patients with NHL (700) as the numerator, rather than the number of positive test results in that group.
- The numerator should be the **True Positives** (400), not the total number of diseased individuals.
*700 / (400 + 400)*
- This calculation uses incorrect values for both the numerator and denominator, not corresponding to the PPV formula.
- The numerator 700 represents the total number of patients with the disease, not those who tested positive, and the denominator incorrectly sums up values that don't represent the proper PPV calculation.
Test characteristics fundamentals US Medical PG Question 6: During an evaluation of a new diagnostic imaging modality for detecting salivary gland tumors, 90 patients tested positive out of the 100 patients who tested positive with the gold standard test. A total of 80 individuals tested negative with the new test out of the 100 individuals who tested negative with the gold standard test. What is the positive likelihood ratio for this test?
- A. 80/90
- B. 90/100
- C. 90/20 (Correct Answer)
- D. 90/110
- E. 10/80
Test characteristics fundamentals Explanation: ***90/20***
- The **positive likelihood ratio (LR+)** is calculated as **sensitivity / (1 - specificity)**. To calculate this, we first need to determine the values for true positives (TP), false positives (FP), true negatives (TN), and false negatives (FN).
- Given that 90 out of 100 actual positive patients tested positive, **TP = 90** and **FN = 100 - 90 = 10**. Also, 80 out of 100 actual negative patients tested negative, so **TN = 80** and **FP = 100 - 80 = 20**.
- **Sensitivity** is the true positive rate (TP / (TP + FN)) = 90 / (90 + 10) = 90 / 100.
- **Specificity** is the true negative rate (TN / (TN + FP)) = 80 / (80 + 20) = 80 / 100.
- Therefore, LR+ = (90/100) / (1 - 80/100) = (90/100) / (20/100) = **90/20**.
*80/90*
- This option incorrectly represents the components for the likelihood ratio. It seems to misinterpret the **true negative** count and the **true positive** count.
- It does not follow the formula for LR+ which is **sensitivity / (1 - specificity)**.
*90/100*
- This value represents the **sensitivity** of the test, which is the proportion of true positives among all actual positives.
- It does not incorporate the **false positive rate** (1 - specificity) in the denominator required for the positive likelihood ratio.
*90/110*
- This option incorrectly combines different values, possibly by confusing the denominator for sensitivity or specificity calculations.
- It does not correspond to the formula for the **positive likelihood ratio**.
*10/80*
- This value seems to relate to the inverse of the **false negative rate** (10/100) or misrepresents the relationship between false negatives and true negatives.
- It is not correctly structured to represent the **positive likelihood ratio (LR+)**.
Test characteristics fundamentals US Medical PG Question 7: You are reviewing raw data from a research study performed at your medical center examining the effectiveness of a novel AIDS screening examination. The study enrolled 250 patients with confirmed AIDS, and 240 of these patients demonstrated a positive screening examination. The control arm of the study enrolled 250 patients who do not have AIDS, and only 5 of these patients tested positive on the novel screening examination. What is the NPV of this novel test?
- A. 240 / (240 + 15)
- B. 240 / (240 + 5)
- C. 240 / (240 + 10)
- D. 245 / (245 + 10) (Correct Answer)
- E. 245 / (245 + 5)
Test characteristics fundamentals Explanation: ***245 / (245 + 10)***
- The **negative predictive value (NPV)** is calculated as **true negatives (TN)** divided by the sum of **true negatives (TN)** and **false negatives (FN)**.
- In this study, there are 250 patients with AIDS; 240 tested positive (true positives, TP), meaning 10 tested negative (false negatives, FN = 250 - 240). There are 250 patients without AIDS; 5 tested positive (false positives, FP), meaning 245 tested negative (true negatives, TN = 250 - 5). Therefore, NPV = 245 / (245 + 10).
*240 / (240 + 15)*
- This calculation incorrectly uses the number of **true positives** (240) in the numerator and denominator, which is relevant for **positive predictive value (PPV)**, not NPV.
- The denominator `(240 + 15)` does not correspond to a valid sum for calculating NPV from the given data.
*240 / (240 + 5)*
- This calculation incorrectly uses **true positives** (240) in the numerator, which is not part of the NPV formula.
- The denominator `(240 + 5)` mixes true positives and false positives, which is incorrect for NPV.
*240 / (240 + 10)*
- This incorrectly places **true positives** (240) in the numerator instead of **true negatives**.
- The denominator `(240+10)` represents **true positives + false negatives**, which is related to sensitivity, not NPV.
*245 / (245 + 5)*
- This calculation correctly identifies **true negatives** (245) in the numerator but incorrectly uses **false positives** (5) in the denominator instead of **false negatives**.
- The denominator for NPV should be **true negatives + false negatives**, which is 245 + 10.
Test characteristics fundamentals US Medical PG Question 8: A pharmaceutical company develops a sequential testing protocol for a rare genetic disorder (prevalence 0.01%). Initial screening test has sensitivity 95% and specificity 90%. Positive results undergo confirmatory testing with sensitivity 99% and specificity 99.5%. The company claims this approach achieves PPV >80% for the final positive result. Evaluate this claim and the rationale for sequential testing in this context.
- A. The claim is true; sequential testing increases PPV by enriching the population tested in the second step (Correct Answer)
- B. The claim is false; sensitivity decreases with sequential testing, reducing PPV
- C. Sequential testing is unnecessary; the first test alone achieves adequate PPV
- D. The claim is false; sequential testing cannot achieve PPV >80% with such low prevalence
- E. The claim is true; the high specificity of the confirmatory test ensures high PPV regardless of prevalence
Test characteristics fundamentals Explanation: ***The claim is true; sequential testing increases PPV by enriching the population tested in the second step***
- Sequential testing works by increasing the **pre-test probability** for the second test, as the cohort being tested has already screened positive once.
- By applying a highly specific confirmatory test to this enriched group, the number of **false positives** is significantly reduced, which drastically improves the **Positive Predictive Value (PPV)**.
*The claim is false; sequential testing cannot achieve PPV >80% with such low prevalence*
- Even with a low **prevalence**, the multiplication of specificities in a sequential process can reduce the **False Positive** rate to a level where the PPV exceeds 80%.
- This line of reasoning ignores that the **denominator** of the PPV calculation (True Positives + False Positives) decreases much faster than the numerator during the second stage.
*The claim is true; the high specificity of the confirmatory test ensures high PPV regardless of prevalence*
- While high **specificity** is crucial, PPV is always dependent on the **prevalence** (pre-test probability) of the condition in the group being tested.
- The claim is true because sequential testing specifically raises that **pre-test probability**, not because prevalence is irrelevant to the calculation.
*The claim is false; sensitivity decreases with sequential testing, reducing PPV*
- It is true that **net sensitivity** decreases in sequential testing, but a decrease in sensitivity actually tends to have a negligible effect on PPV compared to specificity gains.
- **PPV** is primarily driven by the **specificity** and the prevalence in the tested population, both of which are optimized in this two-step protocol.
*Sequential testing is unnecessary; the first test alone achieves adequate PPV*
- Given a prevalence of 0.01% and 90% specificity, the **first test** alone would yield a massive amount of false positives, resulting in a very low PPV (~0.09%).
- A **confirmatory test** is clinically and ethically necessary to avoid wrongly diagnosing thousands of healthy individuals with a **rare genetic disorder**.
Test characteristics fundamentals US Medical PG Question 9: A hospital system is implementing a sepsis screening algorithm using clinical criteria with sensitivity of 92% and specificity of 75%. False positives result in unnecessary antibiotics, cultures, and ICU evaluations costing $3,000 per case. Missing true sepsis cases (false negatives) results in average increased mortality and morbidity costs of $50,000 per case. Hospital sepsis prevalence is 8%. Evaluate the optimal threshold adjustment strategy.
- A. Maintain current threshold as it balances sensitivity and specificity equally
- B. Implement risk stratification with different thresholds for different populations
- C. Abandon screening due to unacceptable false positive rate
- D. Increase threshold to improve specificity and reduce costs from false positives
- E. Decrease threshold to improve sensitivity despite more false positives (Correct Answer)
Test characteristics fundamentals Explanation: ***Decrease threshold to improve sensitivity despite more false positives***
- In sepsis screening, the **cost of a false negative** ($50,000) is nearly 17 times higher than the **cost of a false positive** ($3,000), necessitating a strategy that prioritizes **sensitivity** to minimize missed cases.
- Lowering the threshold further ensures fewer high-cost **mortality and morbidity** events occur, which is the most economically and clinically sound approach given the significant **weighted cost** of missing a diagnosis.
*Increase threshold to improve specificity and reduce costs from false positives*
- Increasing the threshold would increase the number of **false negatives**, leading to massive financial losses due to the $50,000 cost per missed **sepsis case**.
- While it reduces the $3,000 expense of unnecessary **antibiotics and cultures**, the savings are mathematically dwarfed by the increased costs of untreated sepsis.
*Maintain current threshold as it balances sensitivity and specificity equally*
- A balanced threshold is inappropriate when the **consequences of error types** are highly asymmetrical; the algorithm should favor the side with the more severe outcome.
- Simply balancing **sensitivity and specificity** fails to account for the 8% **prevalence** and the extreme disparity in costs between false positives and false negatives.
*Implement risk stratification with different thresholds for different populations*
- While risk stratification is useful, it does not address the fundamental need to minimize **false negatives** across the entire 8% prevalence population.
- This approach adds **operational complexity** without necessarily solving the primary economic imbalance between **screening costs** and mortality costs.
*Abandon screening due to unacceptable false positive rate*
- Abandoning screening would lead to an even higher rate of **missed sepsis cases**, resulting in catastrophic clinical outcomes and **increased hospital liability**.
- The current 75% **specificity** is acceptable because the clinical priority in sepsis is **early detection** to prevent rapid physiological deterioration.
Test characteristics fundamentals US Medical PG Question 10: A 58-year-old man with chronic cough undergoes evaluation for tuberculosis. A tuberculin skin test (TST) is positive (15mm induration). TST has sensitivity of 80% and specificity of 95% in immunocompetent adults. However, he received BCG vaccination as a child in Asia. Local TB prevalence is 0.5%, but his occupational exposure increases his pre-test probability to 10%. Evaluate the most appropriate interpretation and management approach.
- A. Calculate post-test probability and obtain interferon-gamma release assay (IGRA) (Correct Answer)
- B. Repeat TST in 2 weeks to confirm
- C. Treat empirically regardless of test characteristics
- D. Positive test confirms TB; start treatment immediately
- E. False positive due to BCG; no further testing needed
Test characteristics fundamentals Explanation: ***Calculate post-test probability and obtain interferon-gamma release assay (IGRA)***
- In individuals previously vaccinated with **BCG**, the **Tuberculin Skin Test (TST)** can yield **false positives** because the test cross-reacts with BCG antigens, whereas **IGRA** is more specific.
- Clinical decision-making requires integrating **pre-test probability** (10% in this case) with test characteristics to determine **post-test probability** before starting long-term therapy.
*Positive test confirms TB; start treatment immediately*
- A positive **TST** in a patient with a **BCG vaccination** history does not automatically confirm infection; it lacks the specificity to distinguish between vaccination and actual **Mycobacterium tuberculosis** infection.
- Starting **antitubercular therapy** immediately without ruling out a false positive or assessing for **active versus latent disease** violates standard diagnostic protocols.
*False positive due to BCG; no further testing needed*
- While **BCG** causes false positives, the patient’s **occupational exposure** and a significant **15mm induration** make infection plausible; dismissing the result is unsafe.
- High-risk individuals require definitive testing, usually via **IGRA**, to ensure **latent tuberculosis infection (LTBI)** is not overlooked.
*Repeat TST in 2 weeks to confirm*
- Repeating a **TST** within a short window can lead to the **booster effect**, where the second test appears positive due to immunological memory rather than new infection.
- Re-testing with the same diagnostic tool does not solve the underlying issue of **BCG cross-reactivity**; a different, more specific test is required.
*Treat empirically regardless of test characteristics*
- Empirical treatment ignores the potential for **medication toxicity** (e.g., hepatotoxicity from Isoniazid) in a patient who might not actually have **LTBI**.
- Evidence-based medicine requires utilizing **sensitivity, specificity, and prevalence** to justify treatment, especially when more specific tests like **IGRA** are available.
More Test characteristics fundamentals US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.

 curve showing True Positive Rate vs False Positive Rate)
curve showing True Positive Rate vs False Positive Rate)
