Screening test selection criteria US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Screening test selection criteria. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Screening test selection criteria US Medical PG Question 1: A 36-year-old female presents to clinic inquiring about the meaning of a previous negative test result from a new HIV screening test. The efficacy of this new screening test for HIV has been assessed by comparison against existing gold standard detection of HIV RNA via PCR. The study includes 1000 patients, with 850 HIV-negative patients (by PCR) receiving a negative test result, 30 HIV-negative patients receiving a positive test result, 100 HIV positive patients receiving a positive test result, and 20 HIV positive patients receiving a negative test result. Which of the following is most likely to increase the negative predictive value for this test?
- A. Decreased prevalence of HIV in the tested population (Correct Answer)
- B. Increased prevalence of HIV in the tested population
- C. Increased number of false positive test results
- D. Increased number of false negative test results
- E. Decreased number of false positive test results
Screening test selection criteria Explanation: ***Decreased prevalence of HIV in the tested population***
- A **lower prevalence** of a disease in the population means there are fewer actual cases, making a **negative test result** more reliable in ruling out the disease.
- This increases the probability that a person with a negative test truly does not have the disease, thus elevating the **negative predictive value (NPV)**.
*Increased prevalence of HIV in the tested population*
- A **higher prevalence** means there are more actual cases of HIV in the population.
- In this scenario, a negative test result is less reassuring, as there's a greater chance of missing a true positive case, leading to a **decreased NPV**.
*Increased number of false positive test results*
- **False positives** are instances where a test indicates disease when it's not present; they do not directly impact the ability of a negative test to predict absence of disease.
- While they affect the **positive predictive value (PPV)**, they do not directly alter the reliability of a negative result to exclude disease, so the NPV is not increased.
*Increased number of false negative test results*
- **False negatives** occur when a test indicates no disease, but the disease is actually present.
- An increase in false negatives directly implies that a negative test result is less trustworthy, leading to a **decrease in the NPV**.
*Decreased number of false positive test results*
- A decrease in false positive results primarily improves the **positive predictive value (PPV)**.
- While it indicates a more accurate test overall, it does not directly affect NPV, which measures the reliability of a negative test result in ruling out disease.
Screening test selection criteria US Medical PG Question 2: A 25-year-old man with a genetic disorder presents for genetic counseling because he is concerned about the risk that any children he has will have the same disease as himself. Specifically, since childhood he has had difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy. He has also had diarrhea and malabsorption requiring enzyme replacement therapy. If his wife comes from a population where 1 in 10,000 people are affected by this same disorder, which of the following best represents the likelihood a child would be affected as well?
- A. 0.01%
- B. 2%
- C. 0.5%
- D. 1% (Correct Answer)
- E. 50%
Screening test selection criteria Explanation: ***Correct Option: 1%***
- The patient's symptoms (difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy; diarrhea and malabsorption requiring enzyme replacement therapy) are classic for **cystic fibrosis (CF)**, an **autosomal recessive disorder**.
- For an autosomal recessive disorder with a prevalence of 1 in 10,000 in the general population, **q² = 1/10,000**, so **q = 1/100 = 0.01**. The carrier frequency **(2pq)** is approximately **2q = 2 × (1/100) = 1/50 = 0.02**.
- The affected man is **homozygous recessive (aa)** and will always pass on the recessive allele. His wife has a **1/50 chance of being a carrier (Aa)**. If she is a carrier, she has a **1/2 chance of passing on the recessive allele**.
- Therefore, the probability of an affected child = **(Probability wife is a carrier) × (Probability wife passes recessive allele) = 1/50 × 1/2 = 1/100 = 1%**.
*Incorrect Option: 0.01%*
- This percentage is too low and does not correctly account for the carrier frequency in the population and the probability of transmission from a carrier mother.
*Incorrect Option: 2%*
- This represents approximately the carrier frequency (1/50 ≈ 2%), but does not account for the additional 1/2 probability that a carrier mother would pass on the recessive allele.
*Incorrect Option: 0.5%*
- This value would be correct if the carrier frequency were 1/100 instead of 1/50, which does not match the given population prevalence.
*Incorrect Option: 50%*
- **50%** would be the risk if both parents were carriers of an autosomal recessive disorder (1/4 chance = 25% for affected, but if we know one parent passes the allele, conditional probability changes). More accurately, 50% would apply if the disorder were **autosomal dominant** with one affected parent, which is not the case here.
Screening test selection criteria US Medical PG Question 3: A mother presents to the family physician with her 16-year-old son. She explains, "There's something wrong with him doc. His grades are getting worse, he's cutting class, he's gaining weight, and his eyes are often bloodshot." Upon interviewing the patient apart from his mother, he seems withdrawn and angry at times when probed about his social history. The patient denies abuse and sexual history. What initial test should be sent to rule out the most likely culprit of this patient's behavior?
- A. Complete blood count
- B. Sexually transmitted infection (STI) testing
- C. Blood culture
- D. Urine toxicology screen (Correct Answer)
- E. Slit lamp examination
Screening test selection criteria Explanation: ***Urine toxicology screen***
- The patient's presentation with **declining grades**, **cutting class**, **weight gain**, **bloodshot eyes**, and **irritability** are classic signs of **substance abuse** in an adolescent.
- A **urine toxicology screen** is the most appropriate initial test to detect common illicit substances, especially given the clear signs pointing towards drug use.
*Slit lamp examination*
- This test is used to examine the **anterior segment of the eye**, including the conjunctiva, cornea, iris, and lens.
- While the patient has **bloodshot eyes**, this specific test would be more relevant for ruling out ocular infections or injuries, not for diagnosing the underlying cause of systemic behavioral changes.
*Complete blood count*
- A **complete blood count (CBC)** measures different components of the blood, such as red blood cells, white blood cells, and platelets.
- A CBC is a general health indicator and while it can detect infections or anemia, it is not specific or sensitive enough to identify the cause of the behavioral changes described.
*Sexually transmitted infection (STI) testing*
- Although the patient denies sexual history, all adolescents presenting with certain risk factors or symptoms may warrant STI testing in a broader health assessment.
- However, in this scenario, the primary cluster of symptoms (poor grades, cutting class, bloodshot eyes, irritability) points more directly to substance abuse than to an STI.
*Blood culture*
- A **blood culture** is used to detect the presence of bacteria or other microorganisms in the bloodstream, indicating a systemic infection (sepsis).
- The patient's symptoms are not indicative of an acute bacterial bloodstream infection, and a blood culture would not be the initial test for the presented behavioral changes.
Screening test selection criteria US Medical PG Question 4: A novel PET radiotracer is being evaluated for its ability to aid in the diagnosis of Alzheimer’s disease (AD). The study decides to use a sample size of 1,000 patients, and half of the patients enrolled have AD. In the group of patients with AD, 400 are found positive on the novel type of PET imaging examination. In the control group, 50 are found positive. What is the PPV of this novel exam?
- A. 400 / (400+50) (Correct Answer)
- B. 450 / (450 + 100)
- C. 400 / (400+100)
- D. 450 / (450 + 50)
- E. 400 / (400 + 150)
Screening test selection criteria Explanation: ***400 / (400+50)***
- The **Positive Predictive Value (PPV)** is the probability that subjects with a positive test result actually have the disease. It's calculated as **True Positives / (True Positives + False Positives)**.
- In this scenario, **True Positives** are 400 (patients with AD who tested positive), and **False Positives** are 50 (control patients without AD who tested positive).
*450 / (450 + 100)*
- This calculation incorrectly includes **False Negatives** (450, total AD patients - true positives) in the numerator or denominator for PPV, and misidentifies other components.
- The formula for PPV specifically focuses on positive test results and the proportion of those that are truly disease-positive.
*400 / (400+100)*
- This option correctly identifies **True Positives** as 400 but incorrectly assumes **False Positives** are 100.
- The problem states that 50 control patients (without AD) tested positive, which are the false positives.
*450 / (450 + 50)*
- This formula incorrectly uses **450** as the number of **True Positives**, which represents the total number of patients with AD testing positive and negative (400 TP + 100 FN).
- PPV only considers those who tested positive in its numerator.
*400 / (400 + 150)*
- While 400 is correctly identified as **True Positives**, the **False Positives** are incorrectly stated as 150.
- The problem explicitly states that 50 control patients were found positive, making 50 the correct number for false positives.
Screening test selection criteria US Medical PG Question 5: Study X examined the relationship between coffee consumption and lung cancer. The authors of Study X retrospectively reviewed patients' reported coffee consumption and found that drinking greater than 6 cups of coffee per day was associated with an increased risk of developing lung cancer. However, Study X was criticized by the authors of Study Y. Study Y showed that increased coffee consumption was associated with smoking. What type of bias affected Study X, and what study design is geared to reduce the chance of that bias?
- A. Observer bias; double blind analysis
- B. Selection bias; randomization
- C. Lead time bias; placebo
- D. Measurement bias; blinding
- E. Confounding; randomization (Correct Answer)
Screening test selection criteria Explanation: ***Confounding; randomization***
- Study Y suggests that **smoking** is a **confounding variable** because it is associated with both increased coffee consumption (exposure) and increased risk of lung cancer (outcome), distorting the apparent relationship between coffee and lung cancer.
- **Randomization** in experimental studies (such as randomized controlled trials) helps reduce confounding by ensuring that known and unknown confounding factors are evenly distributed among study groups.
- In observational studies where randomization is not possible, confounding can be addressed through **stratification**, **matching**, or **multivariable adjustment** during analysis.
*Observer bias; double blind analysis*
- **Observer bias** occurs when researchers' beliefs or expectations influence the study outcome, which is not the primary issue described here regarding the relationship between coffee, smoking, and lung cancer.
- **Double-blind analysis** is a method to mitigate observer bias by ensuring neither participants nor researchers know who is in the control or experimental groups.
*Selection bias; randomization*
- **Selection bias** happens when the study population is not representative of the target population, leading to inaccurate results, which is not directly indicated by the interaction between coffee and smoking.
- While **randomization** is used to reduce selection bias by creating comparable groups, the core problem identified in Study X is confounding, not flawed participant selection.
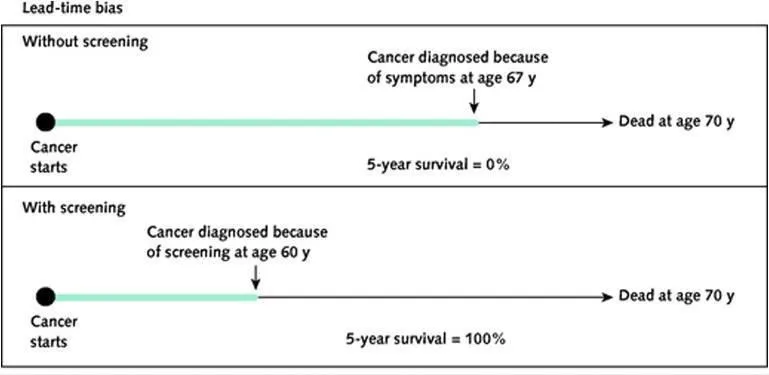
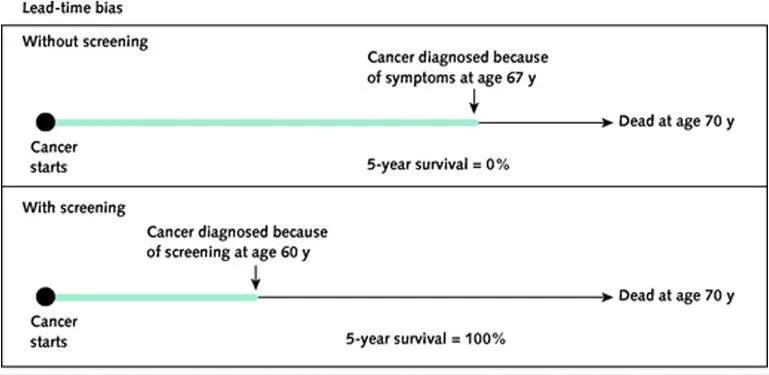
*Lead time bias; placebo*
- **Lead time bias** occurs in screening programs when early detection without improved outcomes makes survival appear longer, an issue unrelated to the described association between coffee, smoking, and lung cancer.
- A **placebo** is an inactive treatment used in clinical trials to control for psychological effects, and its relevance here is limited to treatment intervention studies.
*Measurement bias; blinding*
- **Measurement bias** arises from systematic errors in data collection, such as inaccurate patient reporting of coffee consumption, but the main criticism from Study Y points to a third variable (smoking) affecting the association, not just flawed measurement.
- **Blinding** helps reduce measurement bias by preventing participants or researchers from knowing group assignments, thus minimizing conscious or unconscious influences on data collection.
Screening test selection criteria US Medical PG Question 6: A medical research study is beginning to evaluate the positive predictive value of a novel blood test for non-Hodgkin’s lymphoma. The diagnostic arm contains 700 patients with NHL, of which 400 tested positive for the novel blood test. In the control arm, 700 age-matched control patients are enrolled and 0 are found positive for the novel test. What is the PPV of this test?
- A. 400 / (400 + 0) (Correct Answer)
- B. 700 / (700 + 300)
- C. 400 / (400 + 300)
- D. 700 / (700 + 0)
- E. 700 / (400 + 400)
Screening test selection criteria Explanation: ***400 / (400 + 0) = 1.0 or 100%***
- The **positive predictive value (PPV)** is calculated as **True Positives / (True Positives + False Positives)**.
- In this scenario, **True Positives (TP)** are the 400 patients with NHL who tested positive, and **False Positives (FP)** are 0, as no control patients tested positive.
- This gives a PPV of 400/400 = **1.0 or 100%**, indicating that all patients who tested positive actually had the disease.
*700 / (700 + 300)*
- This calculation does not align with the formula for PPV based on the given data.
- The denominator `(700+300)` suggests an incorrect combination of various patient groups.
*400 / (400 + 300)*
- The denominator `(400+300)` incorrectly includes 300, which is the number of **False Negatives** (patients with NHL who tested negative), not False Positives.
- PPV focuses on the proportion of true positives among all positive tests, not all diseased individuals.
*700 / (700 + 0)*
- This calculation incorrectly uses the total number of patients with NHL (700) as the numerator, rather than the number of positive test results in that group.
- The numerator should be the **True Positives** (400), not the total number of diseased individuals.
*700 / (400 + 400)*
- This calculation uses incorrect values for both the numerator and denominator, not corresponding to the PPV formula.
- The numerator 700 represents the total number of patients with the disease, not those who tested positive, and the denominator incorrectly sums up values that don't represent the proper PPV calculation.
Screening test selection criteria US Medical PG Question 7: Two studies are reviewed for submission to an oncology journal. In Study A, a novel MRI technology is evaluated as a screening tool for ovarian cancer. The authors find that the mean survival time is 4 years in the control group and 10 years in the MRI-screened group. In Study B, cognitive behavioral therapy (CBT) and a novel antidepressant are used to treat patients with comorbid pancreatic cancer and major depression. Patients receiving the new drug are told that they are expected to have quick resolution of their depression, while those who do not receive the drug are not told anything about their prognosis. Which of the following describes the likely type of bias in Study A and Study B?
- A. Latency Bias; Golem effect
- B. Confounding; Golem effect
- C. Lead time bias; Golem effect
- D. Lead time bias; Pygmalion effect (Correct Answer)
- E. Latency bias; Pygmalion effect
Screening test selection criteria Explanation: ***Lead time bias; Pygmalion effect***
- In Study A, the MRI technology detects ovarian cancer earlier, artificially making the survival time appear longer simply due to earlier diagnosis, not necessarily improved outcomes, which is characteristic of **lead time bias**.
- In Study B, the patients receiving the new drug are told to expect quick resolution of their depression, leading to increased expectation of improvement, which describes the **Pygmalion effect** (a form of observer-expectancy effect where higher expectations lead to increased performance).
*Latency Bias; Golem effect*
- **Latency bias** refers to a delay in the manifestation of an outcome, which is not the primary issue in Study A's screening context.
- The **Golem effect** is a form of negative self-fulfilling prophecy where lower expectations placed upon individuals by superiors/researchers lead to poorer performance, which is opposite to what is described in Study B.
*Confounding; Golem effect*
- **Confounding** occurs when an unmeasured third variable is associated with both the exposure and the outcome, distorting the observed relationship; while confounding is common, the scenario in Study A specifically points to a screening effect on survival time.
- As mentioned, the **Golem effect** refers to negative expectations leading to poorer outcomes, which is not present in Study B.
*Lead time bias; Golem effect*
- **Lead time bias** correctly identifies the issue in Study A, as explaining the apparently longer survival as a result of earlier detection.
- However, the **Golem effect** incorrectly describes the scenario in Study B, where positive expectations are given, not negative ones.
*Latency bias; Pygmalion effect*
- **Latency bias** is not the primary bias described in Study A; the immediate impact of early detection on survival statistics points to lead time bias.
- The **Pygmalion effect** correctly describes the bias in Study B, where positive expectations from the researchers influence patient outcomes.
Screening test selection criteria US Medical PG Question 8: A student health coordinator plans on leading a campus-wide HIV screening program that will be free for the entire undergraduate student body. The goal is to capture as many correct HIV diagnoses as possible with the fewest false positives. The coordinator consults with the hospital to see which tests are available to use for this program. Test A has a sensitivity of 0.92 and a specificity of 0.99. Test B has a sensitivity of 0.95 and a specificity of 0.96. Test C has a sensitivity of 0.98 and a specificity of 0.93. Which of the following testing schemes should the coordinator pursue?
- A. Test A on the entire student body followed by Test B on those who are positive
- B. Test A on the entire student body followed by Test C on those who are positive
- C. Test C on the entire student body followed by Test B on those who are positive
- D. Test C on the entire student body followed by Test A on those who are positive (Correct Answer)
- E. Test B on the entire student body followed by Test A on those who are positive
Screening test selection criteria Explanation: ***Test C on the entire student body followed by Test A on those who are positive***
- To "capture as many correct HIV diagnoses as possible" (maximize true positives), the initial screening test should have the **highest sensitivity**. Test C has the highest sensitivity (0.98).
- To "capture as few false positives as possible" (maximize true negatives and confirm diagnoses), the confirmatory test should have the **highest specificity**. Test A has the highest specificity (0.99).
*Test A on the entire student body followed by Test B on those who are positive*
- Starting with Test A (sensitivity 0.92) would miss more true positive cases than starting with Test C (sensitivity 0.98), failing the goal of **capturing as many cases as possible**.
- Following with Test B (specificity 0.96) would result in more false positives than following with Test A (specificity 0.99).
*Test A on the entire student body followed by Test C on those who are positive*
- This scheme would miss many true positive cases initially due to Test A's lower sensitivity compared to Test C.
- Following with Test C would introduce more false positives than necessary, as it has a lower specificity (0.93) than Test A (0.99).
*Test C on the entire student body followed by Test B on those who are positive*
- While Test C is a good initial screen for its high sensitivity, following it with Test B (specificity 0.96) is less optimal than Test A (specificity 0.99) for minimizing false positives in the confirmation step.
- This combination would therefore yield more false positives in the confirmatory stage than using Test A.
*Test B on the entire student body followed by Test A on those who are positive*
- Test B has a sensitivity of 0.95, which is lower than Test C's sensitivity of 0.98, meaning it would miss more true positive cases at the initial screening stage.
- While Test A provides excellent specificity for confirmation, the initial screening step is suboptimal for the goal of capturing as many diagnoses as possible.
Screening test selection criteria US Medical PG Question 9: You are currently employed as a clinical researcher working on clinical trials of a new drug to be used for the treatment of Parkinson's disease. Currently, you have already determined the safe clinical dose of the drug in a healthy patient. You are in the phase of drug development where the drug is studied in patients with the target disease to determine its efficacy. Which of the following phases is this new drug currently in?
- A. Phase 4
- B. Phase 1
- C. Phase 2 (Correct Answer)
- D. Phase 0
- E. Phase 3
Screening test selection criteria Explanation: ***Phase 2***
- **Phase 2 trials** involve studying the drug in patients with the target disease to assess its **efficacy** and further evaluate safety, typically involving a few hundred patients.
- The question describes a stage after safe dosing in healthy patients (Phase 1) and before large-scale efficacy confirmation (Phase 3), focusing on efficacy in the target population.
*Phase 4*
- **Phase 4 trials** occur **after a drug has been approved** and marketed, monitoring long-term effects, optimal use, and rare side effects in a diverse patient population.
- This phase is conducted post-market approval, whereas the question describes a drug still in development prior to approval.
*Phase 1*
- **Phase 1 trials** primarily focus on determining the **safety and dosage** of a new drug in a **small group of healthy volunteers** (or sometimes patients with advanced disease if the drug is highly toxic).
- The question states that the safe clinical dose in a healthy patient has already been determined, indicating that Phase 1 has been completed.
*Phase 0*
- **Phase 0 trials** are exploratory, very early-stage studies designed to confirm that the drug reaches the target and acts as intended, typically involving a very small number of doses and participants.
- These trials are conducted much earlier in the development process, preceding the determination of safe clinical doses and large-scale efficacy studies.
*Phase 3*
- **Phase 3 trials** are large-scale studies involving hundreds to thousands of patients to confirm **efficacy**, monitor side effects, compare it to commonly used treatments, and collect information that will allow the drug to be used safely.
- While Phase 3 does assess efficacy, it follows Phase 2 and is typically conducted on a much larger scale before submitting for regulatory approval.
Screening test selection criteria US Medical PG Question 10: A pharmaceutical company develops a sequential testing protocol for a rare genetic disorder (prevalence 0.01%). Initial screening test has sensitivity 95% and specificity 90%. Positive results undergo confirmatory testing with sensitivity 99% and specificity 99.5%. The company claims this approach achieves PPV >80% for the final positive result. Evaluate this claim and the rationale for sequential testing in this context.
- A. The claim is true; sequential testing increases PPV by enriching the population tested in the second step (Correct Answer)
- B. The claim is false; sensitivity decreases with sequential testing, reducing PPV
- C. Sequential testing is unnecessary; the first test alone achieves adequate PPV
- D. The claim is false; sequential testing cannot achieve PPV >80% with such low prevalence
- E. The claim is true; the high specificity of the confirmatory test ensures high PPV regardless of prevalence
Screening test selection criteria Explanation: ***The claim is true; sequential testing increases PPV by enriching the population tested in the second step***
- Sequential testing works by increasing the **pre-test probability** for the second test, as the cohort being tested has already screened positive once.
- By applying a highly specific confirmatory test to this enriched group, the number of **false positives** is significantly reduced, which drastically improves the **Positive Predictive Value (PPV)**.
*The claim is false; sequential testing cannot achieve PPV >80% with such low prevalence*
- Even with a low **prevalence**, the multiplication of specificities in a sequential process can reduce the **False Positive** rate to a level where the PPV exceeds 80%.
- This line of reasoning ignores that the **denominator** of the PPV calculation (True Positives + False Positives) decreases much faster than the numerator during the second stage.
*The claim is true; the high specificity of the confirmatory test ensures high PPV regardless of prevalence*
- While high **specificity** is crucial, PPV is always dependent on the **prevalence** (pre-test probability) of the condition in the group being tested.
- The claim is true because sequential testing specifically raises that **pre-test probability**, not because prevalence is irrelevant to the calculation.
*The claim is false; sensitivity decreases with sequential testing, reducing PPV*
- It is true that **net sensitivity** decreases in sequential testing, but a decrease in sensitivity actually tends to have a negligible effect on PPV compared to specificity gains.
- **PPV** is primarily driven by the **specificity** and the prevalence in the tested population, both of which are optimized in this two-step protocol.
*Sequential testing is unnecessary; the first test alone achieves adequate PPV*
- Given a prevalence of 0.01% and 90% specificity, the **first test** alone would yield a massive amount of false positives, resulting in a very low PPV (~0.09%).
- A **confirmatory test** is clinically and ethically necessary to avoid wrongly diagnosing thousands of healthy individuals with a **rare genetic disorder**.
More Screening test selection criteria US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.