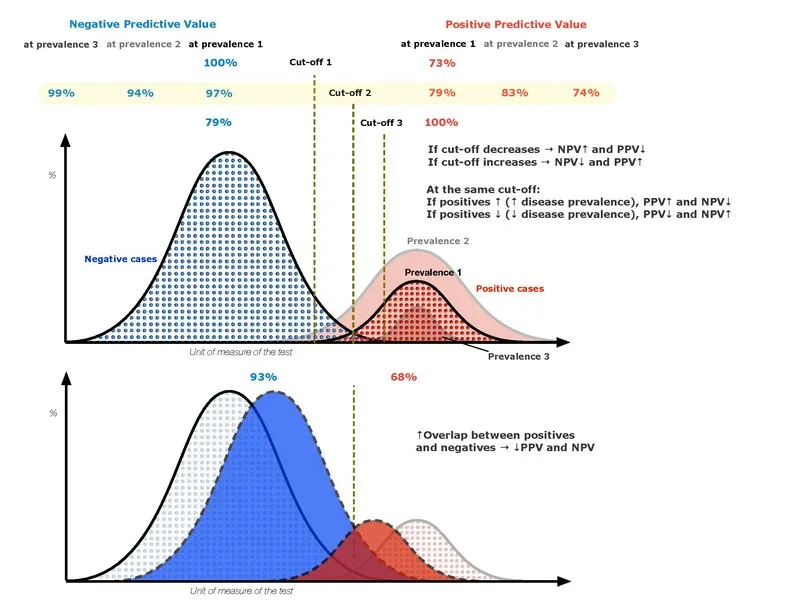
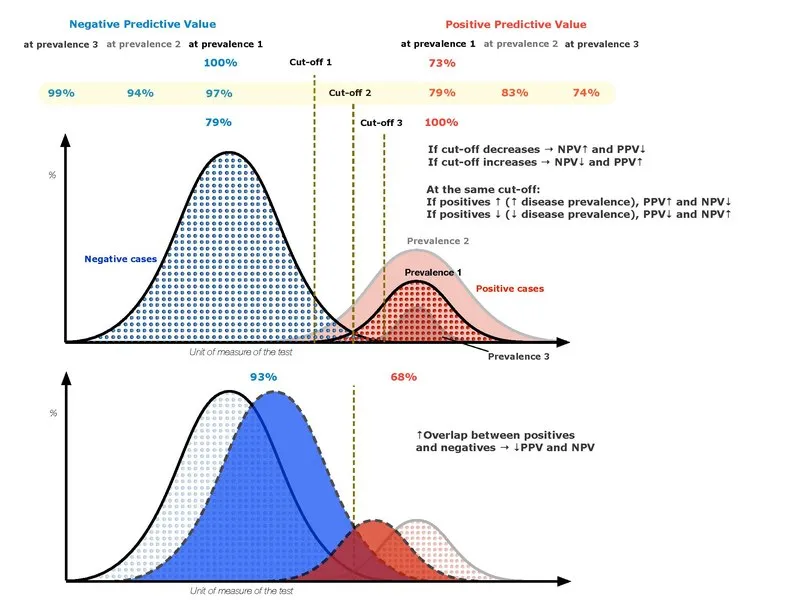
Prevalence effects on predictive values US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Prevalence effects on predictive values. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Prevalence effects on predictive values US Medical PG Question 1: A 25-year-old man with a genetic disorder presents for genetic counseling because he is concerned about the risk that any children he has will have the same disease as himself. Specifically, since childhood he has had difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy. He has also had diarrhea and malabsorption requiring enzyme replacement therapy. If his wife comes from a population where 1 in 10,000 people are affected by this same disorder, which of the following best represents the likelihood a child would be affected as well?
- A. 0.01%
- B. 2%
- C. 0.5%
- D. 1% (Correct Answer)
- E. 50%
Prevalence effects on predictive values Explanation: ***Correct Option: 1%***
- The patient's symptoms (difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy; diarrhea and malabsorption requiring enzyme replacement therapy) are classic for **cystic fibrosis (CF)**, an **autosomal recessive disorder**.
- For an autosomal recessive disorder with a prevalence of 1 in 10,000 in the general population, **q² = 1/10,000**, so **q = 1/100 = 0.01**. The carrier frequency **(2pq)** is approximately **2q = 2 × (1/100) = 1/50 = 0.02**.
- The affected man is **homozygous recessive (aa)** and will always pass on the recessive allele. His wife has a **1/50 chance of being a carrier (Aa)**. If she is a carrier, she has a **1/2 chance of passing on the recessive allele**.
- Therefore, the probability of an affected child = **(Probability wife is a carrier) × (Probability wife passes recessive allele) = 1/50 × 1/2 = 1/100 = 1%**.
*Incorrect Option: 0.01%*
- This percentage is too low and does not correctly account for the carrier frequency in the population and the probability of transmission from a carrier mother.
*Incorrect Option: 2%*
- This represents approximately the carrier frequency (1/50 ≈ 2%), but does not account for the additional 1/2 probability that a carrier mother would pass on the recessive allele.
*Incorrect Option: 0.5%*
- This value would be correct if the carrier frequency were 1/100 instead of 1/50, which does not match the given population prevalence.
*Incorrect Option: 50%*
- **50%** would be the risk if both parents were carriers of an autosomal recessive disorder (1/4 chance = 25% for affected, but if we know one parent passes the allele, conditional probability changes). More accurately, 50% would apply if the disorder were **autosomal dominant** with one affected parent, which is not the case here.
Prevalence effects on predictive values US Medical PG Question 2: A scientist in Boston is studying a new blood test to detect Ab to the parainfluenza virus with increased sensitivity and specificity. So far, her best attempt at creating such an exam reached 82% sensitivity and 88% specificity. She is hoping to increase these numbers by at least 2 percent for each value. After several years of work, she believes that she has actually managed to reach a sensitivity and specificity even greater than what she had originally hoped for. She travels to South America to begin testing her newest blood test. She finds 2,000 patients who are willing to participate in her study. Of the 2,000 patients, 1,200 of them are known to be infected with the parainfluenza virus. The scientist tests these 1,200 patients’ blood and finds that only 120 of them tested negative with her new test. Of the following options, which describes the sensitivity of the test?
- A. 82%
- B. 86%
- C. 98%
- D. 90% (Correct Answer)
- E. 84%
Prevalence effects on predictive values Explanation: ***90%***
- **Sensitivity** is calculated as the number of **true positives** divided by the total number of individuals with the disease (true positives + false negatives).
- In this scenario, there were 1200 infected patients (total diseased), and 120 of them tested negative (false negatives). Therefore, 1200 - 120 = 1080 patients tested positive (true positives). The sensitivity is 1080 / 1200 = 0.90, or **90%**.
*82%*
- This value was the **original sensitivity** of the test before the scientist improved it.
- The question states that the scientist believes she has achieved a sensitivity "even greater than what she had originally hoped for."
*86%*
- This value is not directly derivable from the given data for the new test's sensitivity.
- It might represent an intermediate calculation or an incorrect interpretation of the provided numbers.
*98%*
- This would imply only 24 false negatives out of 1200 true disease cases, which is not the case (120 false negatives).
- A sensitivity of 98% would be significantly higher than the calculated 90% and the initial stated values.
*84%*
- This value is not derived from the presented data regarding the new test's performance.
- It could be mistaken for an attempt to add 2% to the original 82% sensitivity, but the actual data from the new test should be used.
Prevalence effects on predictive values US Medical PG Question 3: A 43-year-old woman presents to her primary care physician with complaints of mild shortness of breath and right-sided chest pain for three days. She reports that lately she has had a nagging nonproductive cough and low-grade fevers. On examination, her vital signs are: temperature 99.1 deg F (37.3 deg C), blood pressure is 115/70 mmHg, pulse is 91/min, respirations are 17/min, and oxygen saturation 97% on room air. She is well-appearing, with normal work of breathing, and no leg swelling. She is otherwise healthy, with no prior medical or surgical history, currently taking no medications. The attending has a low suspicion for the most concerning diagnosis and would like to exclude it with a very sensitive though non-specific test. Which of the following should this physician order?
- A. Obtain chest radiograph
- B. Obtain spiral CT chest with IV contrast
- C. Order a lower extremity ultrasound
- D. Order a D-dimer (Correct Answer)
- E. Obtain ventilation-perfusion scan
Prevalence effects on predictive values Explanation: ***Order a D-dimer***
- The physician has a **low suspicion based on clinical assessment** and wants to **exclude** a concerning diagnosis (likely **pulmonary embolism** or PE) using a **sensitive test**. A negative D-dimer test can effectively rule out PE in patients with a low pre-test probability.
- The D-dimer is a product of **fibrin degradation** and its elevation indicates recent or ongoing **thrombus formation** and lysis. It is highly sensitive for PE but has low specificity.
*Obtain chest radiograph*
- A chest radiograph is often **normal in pulmonary embolism** or may show non-specific findings, making it unsuitable for ruling out PE.
- While useful for diagnosing other conditions like pneumonia or pleural effusions, it is **not sensitive enough to exclude PE**.
*Obtain spiral CT chest with IV contrast*
- A **spiral CT chest with IV contrast (CT pulmonary angiography)** is the gold standard for diagnosing PE, but it is **not a sensitive rule-out test** for low-probability cases.
- It involves **radiation exposure** and **contrast administration**, which are generally avoided if a less invasive, equally effective rule-out test is available for low-risk patients.
*Order a lower extremity ultrasound*
- Lower extremity ultrasound is used to diagnose **deep vein thrombosis (DVT)**, which is a common source of PE.
- While DVT can lead to PE, a negative lower extremity ultrasound **does not rule out PE** itself, as the clot may have already embolized or originated from elsewhere.
*Obtain ventilation-perfusion scan*
- A **ventilation-perfusion (V/Q) scan** is an alternative to CT angiography for diagnosing PE, particularly in patients with contraindications to contrast.
- However, it is **less definitive than CTPA** and is typically used when suspicion for PE is moderate or higher, rather than as a primary rule-out test for low-probability patients.
Prevalence effects on predictive values US Medical PG Question 4: A 6-month-old male presents for a routine visit to his pediatrician. Two months ago, the patient was seen for tachypnea and wheezing, and diagnosed with severe respiratory syncytial virus (RSV) bronchiolitis. After admission to the hospital and supportive care, the patient recovered and currently is not experiencing any trouble breathing. Regarding the possibility of future reactive airway disease, which of the following statements is most accurate?
- A. “There is no clear relationship between RSV and the development of asthma.”
- B. “Your child has a greater than 20% chance of developing asthma” (Correct Answer)
- C. “Your child’s risk of asthma is less than the general population.”
- D. “Your child has a less than 5% chance of developing asthma”
- E. “Your child’s risk of asthma is the same as the general population.”
Prevalence effects on predictive values Explanation: ***“Your child has a greater than 20% chance of developing asthma”***
- Severe **RSV bronchiolitis** in infancy is a significant risk factor for the development of **recurrent wheezing** and **childhood asthma**.
- Studies estimate that a substantial proportion, often greater than 20%, of infants with severe RSV bronchiolitis will go on to develop **asthma** later in childhood.
*“There is no clear relationship between RSV and the development of asthma.”*
- This statement is incorrect as there is a **well-established link** between severe RSV infection in early life and an increased risk of developing **asthma**.
- Numerous epidemiological and longitudinal studies have documented this association.
*“Your child’s risk of asthma is less than the general population.”*
- This is incorrect, as severe RSV infection **increases** the risk of asthma, not decreases it.
- Children with a history of severe RSV have a **higher incidence** of asthma compared to the general pediatric population.
*“Your child has a less than 5% chance of developing asthma”*
- This percentage is **too low** given the known association between severe RSV bronchiolitis and subsequent asthma.
- The actual risk is considerably higher, typically falling into the range of 20-50% for those with severe RSV.
*“Your child’s risk of asthma is the same as the general population.”*
- This statement is inaccurate because severe RSV infection in infancy is a recognized independent **risk factor** for **asthma development**.
- Therefore, the child's risk is elevated above that of the general population.
Prevalence effects on predictive values US Medical PG Question 5: A novel PET radiotracer is being evaluated for its ability to aid in the diagnosis of Alzheimer’s disease (AD). The study decides to use a sample size of 1,000 patients, and half of the patients enrolled have AD. In the group of patients with AD, 400 are found positive on the novel type of PET imaging examination. In the control group, 50 are found positive. What is the PPV of this novel exam?
- A. 400 / (400+50) (Correct Answer)
- B. 450 / (450 + 100)
- C. 400 / (400+100)
- D. 450 / (450 + 50)
- E. 400 / (400 + 150)
Prevalence effects on predictive values Explanation: ***400 / (400+50)***
- The **Positive Predictive Value (PPV)** is the probability that subjects with a positive test result actually have the disease. It's calculated as **True Positives / (True Positives + False Positives)**.
- In this scenario, **True Positives** are 400 (patients with AD who tested positive), and **False Positives** are 50 (control patients without AD who tested positive).
*450 / (450 + 100)*
- This calculation incorrectly includes **False Negatives** (450, total AD patients - true positives) in the numerator or denominator for PPV, and misidentifies other components.
- The formula for PPV specifically focuses on positive test results and the proportion of those that are truly disease-positive.
*400 / (400+100)*
- This option correctly identifies **True Positives** as 400 but incorrectly assumes **False Positives** are 100.
- The problem states that 50 control patients (without AD) tested positive, which are the false positives.
*450 / (450 + 50)*
- This formula incorrectly uses **450** as the number of **True Positives**, which represents the total number of patients with AD testing positive and negative (400 TP + 100 FN).
- PPV only considers those who tested positive in its numerator.
*400 / (400 + 150)*
- While 400 is correctly identified as **True Positives**, the **False Positives** are incorrectly stated as 150.
- The problem explicitly states that 50 control patients were found positive, making 50 the correct number for false positives.
Prevalence effects on predictive values US Medical PG Question 6: A medical research study is beginning to evaluate the positive predictive value of a novel blood test for non-Hodgkin’s lymphoma. The diagnostic arm contains 700 patients with NHL, of which 400 tested positive for the novel blood test. In the control arm, 700 age-matched control patients are enrolled and 0 are found positive for the novel test. What is the PPV of this test?
- A. 400 / (400 + 0) (Correct Answer)
- B. 700 / (700 + 300)
- C. 400 / (400 + 300)
- D. 700 / (700 + 0)
- E. 700 / (400 + 400)
Prevalence effects on predictive values Explanation: ***400 / (400 + 0) = 1.0 or 100%***
- The **positive predictive value (PPV)** is calculated as **True Positives / (True Positives + False Positives)**.
- In this scenario, **True Positives (TP)** are the 400 patients with NHL who tested positive, and **False Positives (FP)** are 0, as no control patients tested positive.
- This gives a PPV of 400/400 = **1.0 or 100%**, indicating that all patients who tested positive actually had the disease.
*700 / (700 + 300)*
- This calculation does not align with the formula for PPV based on the given data.
- The denominator `(700+300)` suggests an incorrect combination of various patient groups.
*400 / (400 + 300)*
- The denominator `(400+300)` incorrectly includes 300, which is the number of **False Negatives** (patients with NHL who tested negative), not False Positives.
- PPV focuses on the proportion of true positives among all positive tests, not all diseased individuals.
*700 / (700 + 0)*
- This calculation incorrectly uses the total number of patients with NHL (700) as the numerator, rather than the number of positive test results in that group.
- The numerator should be the **True Positives** (400), not the total number of diseased individuals.
*700 / (400 + 400)*
- This calculation uses incorrect values for both the numerator and denominator, not corresponding to the PPV formula.
- The numerator 700 represents the total number of patients with the disease, not those who tested positive, and the denominator incorrectly sums up values that don't represent the proper PPV calculation.
Prevalence effects on predictive values US Medical PG Question 7: A public health campaign increases vaccination rates against human papillomaviruses 16 and 18. Increased vaccination rates would have which of the following effects on the Papanicolaou test?
- A. Decreased true positive rate
- B. Decreased positive predictive value (Correct Answer)
- C. Decreased negative predictive value
- D. Increased positive likelihood ratio
- E. Increased true negative rate
Prevalence effects on predictive values Explanation: ***Decreased positive predictive value***
- An increase in vaccination rates against **HPV 16 and 18** will reduce the **prevalence of cervical dysplasia and cancer** caused by these types.
- With fewer true cases in the population, a Papanicolaou (Pap) test is more likely to yield a **false positive result** when it tests positive, thus decreasing its **positive predictive value**.
- **PPV = TP/(TP+FP)** - when disease prevalence decreases, the number of true positives decreases while false positives remain relatively stable, reducing the overall PPV.
*Decreased true positive rate*
- The **true positive rate (sensitivity)** of the Pap test refers to its ability to correctly identify individuals with the disease (cervical dysplasia/cancer).
- While the overall number of true positives will decrease due to reduced disease prevalence, the inherent ability of the test to detect existing disease (i.e., its sensitivity) is **not directly affected by vaccination rates**.
- Sensitivity is an intrinsic test property: **Sensitivity = TP/(TP+FN)**.
*Decreased negative predictive value*
- The **negative predictive value** is the probability that a person with a negative test result truly does not have the disease.
- As the prevalence of the disease decreases due to vaccination, the probability of a negative test being truly negative actually **increases**, leading to an **increased negative predictive value**.
- **NPV = TN/(TN+FN)** - lower prevalence means fewer false negatives relative to true negatives.
*Increased positive likelihood ratio*
- The **positive likelihood ratio** describes how much more likely a positive test result is in someone with the disease compared to someone without the disease and is derived from sensitivity and specificity.
- **LR+ = Sensitivity/(1-Specificity)** - vaccination reduces disease prevalence but does not inherently change the **diagnostic accuracy** (sensitivity and specificity) of the Pap test, so the likelihood ratio remains unchanged.
*Increased true negative rate*
- The **true negative rate (specificity)** of the Pap test refers to its ability to correctly identify individuals who do not have the disease.
- While the overall number of true negatives will increase (because there are fewer cases to begin with), the inherent ability of the test to correctly identify healthy individuals (i.e., its specificity) is **not directly affected by the change in disease prevalence**.
- Specificity is an intrinsic test property: **Specificity = TN/(TN+FP)**.
Prevalence effects on predictive values US Medical PG Question 8: An office team is being observed by an outside agency at the request of management to make sure they are completing all their tasks appropriately. Several of the employees are nervous that they are being watched and take care to perform their jobs with extra care, more so than they would have done during a normal workday. What best describes this behavior?
- A. Pygmalion effect
- B. Novelty effect
- C. Hawthorne effect (Correct Answer)
- D. Observer bias
- E. Ringelmann effect
Prevalence effects on predictive values Explanation: ***Hawthorne effect***
- The **Hawthorne effect** describes changes in behavior that occur among individuals who are aware that they are being observed.
- In this scenario, the employees' increased diligence due to being watched by an outside agency aligns perfectly with this psychological phenomenon.
*Pygmalion effect*
- The **Pygmalion effect** refers to the phenomenon where higher expectations lead to improved performance in a given area.
- It focuses on how an observer's expectations can influence the subject's behavior, rather than the subject's awareness of observation itself.
*Novelty effect*
- The **novelty effect** occurs when the initial interest or enthusiasm for a new item or intervention temporarily improves performance, which then wanes over time.
- This effect is related to the newness of a situation, not the act of being observed.
*Observer bias*
- **Observer bias** (also known as ascertainment bias) happens when the observer's expectations, beliefs, or preconceptions influence how they perceive or record data.
- It refers to a bias in the *observer*, not a change in the *observed subject's behavior* due to being watched.
*Ringelmann effect*
- The **Ringelmann effect** (or social loafing) describes the tendency for individual members of a group to become less productive as the size of their group increases.
- This is a phenomenon of reduced individual effort in a group setting, not an alteration in behavior due to being observed.
Prevalence effects on predictive values US Medical PG Question 9: A pharmaceutical company develops a sequential testing protocol for a rare genetic disorder (prevalence 0.01%). Initial screening test has sensitivity 95% and specificity 90%. Positive results undergo confirmatory testing with sensitivity 99% and specificity 99.5%. The company claims this approach achieves PPV >80% for the final positive result. Evaluate this claim and the rationale for sequential testing in this context.
- A. The claim is true; sequential testing increases PPV by enriching the population tested in the second step (Correct Answer)
- B. The claim is false; sensitivity decreases with sequential testing, reducing PPV
- C. Sequential testing is unnecessary; the first test alone achieves adequate PPV
- D. The claim is false; sequential testing cannot achieve PPV >80% with such low prevalence
- E. The claim is true; the high specificity of the confirmatory test ensures high PPV regardless of prevalence
Prevalence effects on predictive values Explanation: ***The claim is true; sequential testing increases PPV by enriching the population tested in the second step***
- Sequential testing works by increasing the **pre-test probability** for the second test, as the cohort being tested has already screened positive once.
- By applying a highly specific confirmatory test to this enriched group, the number of **false positives** is significantly reduced, which drastically improves the **Positive Predictive Value (PPV)**.
*The claim is false; sequential testing cannot achieve PPV >80% with such low prevalence*
- Even with a low **prevalence**, the multiplication of specificities in a sequential process can reduce the **False Positive** rate to a level where the PPV exceeds 80%.
- This line of reasoning ignores that the **denominator** of the PPV calculation (True Positives + False Positives) decreases much faster than the numerator during the second stage.
*The claim is true; the high specificity of the confirmatory test ensures high PPV regardless of prevalence*
- While high **specificity** is crucial, PPV is always dependent on the **prevalence** (pre-test probability) of the condition in the group being tested.
- The claim is true because sequential testing specifically raises that **pre-test probability**, not because prevalence is irrelevant to the calculation.
*The claim is false; sensitivity decreases with sequential testing, reducing PPV*
- It is true that **net sensitivity** decreases in sequential testing, but a decrease in sensitivity actually tends to have a negligible effect on PPV compared to specificity gains.
- **PPV** is primarily driven by the **specificity** and the prevalence in the tested population, both of which are optimized in this two-step protocol.
*Sequential testing is unnecessary; the first test alone achieves adequate PPV*
- Given a prevalence of 0.01% and 90% specificity, the **first test** alone would yield a massive amount of false positives, resulting in a very low PPV (~0.09%).
- A **confirmatory test** is clinically and ethically necessary to avoid wrongly diagnosing thousands of healthy individuals with a **rare genetic disorder**.
Prevalence effects on predictive values US Medical PG Question 10: A hospital system is implementing a sepsis screening algorithm using clinical criteria with sensitivity of 92% and specificity of 75%. False positives result in unnecessary antibiotics, cultures, and ICU evaluations costing $3,000 per case. Missing true sepsis cases (false negatives) results in average increased mortality and morbidity costs of $50,000 per case. Hospital sepsis prevalence is 8%. Evaluate the optimal threshold adjustment strategy.
- A. Maintain current threshold as it balances sensitivity and specificity equally
- B. Implement risk stratification with different thresholds for different populations
- C. Abandon screening due to unacceptable false positive rate
- D. Increase threshold to improve specificity and reduce costs from false positives
- E. Decrease threshold to improve sensitivity despite more false positives (Correct Answer)
Prevalence effects on predictive values Explanation: ***Decrease threshold to improve sensitivity despite more false positives***
- In sepsis screening, the **cost of a false negative** ($50,000) is nearly 17 times higher than the **cost of a false positive** ($3,000), necessitating a strategy that prioritizes **sensitivity** to minimize missed cases.
- Lowering the threshold further ensures fewer high-cost **mortality and morbidity** events occur, which is the most economically and clinically sound approach given the significant **weighted cost** of missing a diagnosis.
*Increase threshold to improve specificity and reduce costs from false positives*
- Increasing the threshold would increase the number of **false negatives**, leading to massive financial losses due to the $50,000 cost per missed **sepsis case**.
- While it reduces the $3,000 expense of unnecessary **antibiotics and cultures**, the savings are mathematically dwarfed by the increased costs of untreated sepsis.
*Maintain current threshold as it balances sensitivity and specificity equally*
- A balanced threshold is inappropriate when the **consequences of error types** are highly asymmetrical; the algorithm should favor the side with the more severe outcome.
- Simply balancing **sensitivity and specificity** fails to account for the 8% **prevalence** and the extreme disparity in costs between false positives and false negatives.
*Implement risk stratification with different thresholds for different populations*
- While risk stratification is useful, it does not address the fundamental need to minimize **false negatives** across the entire 8% prevalence population.
- This approach adds **operational complexity** without necessarily solving the primary economic imbalance between **screening costs** and mortality costs.
*Abandon screening due to unacceptable false positive rate*
- Abandoning screening would lead to an even higher rate of **missed sepsis cases**, resulting in catastrophic clinical outcomes and **increased hospital liability**.
- The current 75% **specificity** is acceptable because the clinical priority in sepsis is **early detection** to prevent rapid physiological deterioration.
More Prevalence effects on predictive values US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.