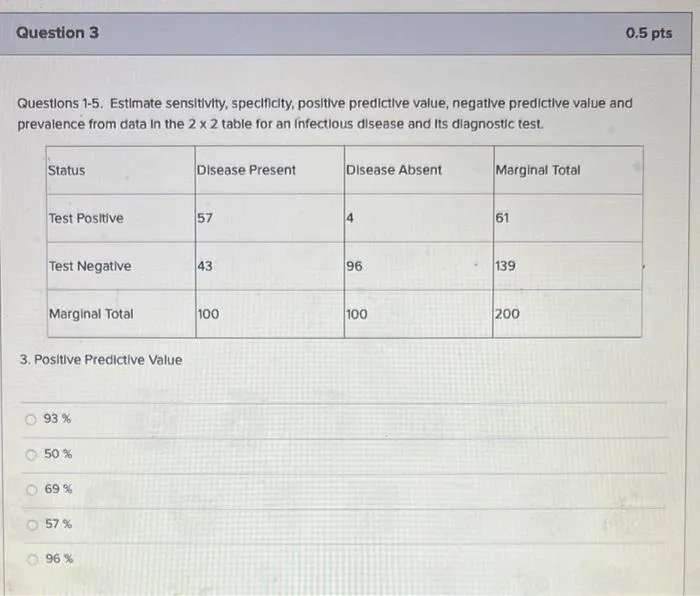
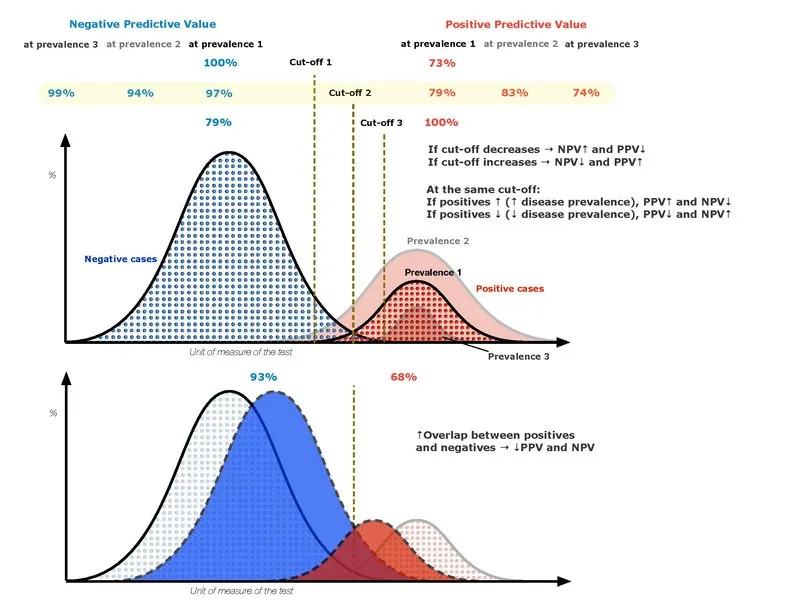
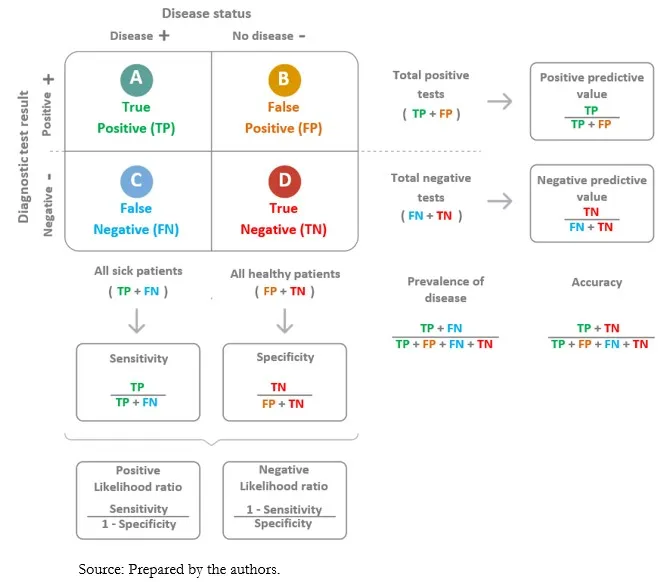
Positive predictive value US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Positive predictive value. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Positive predictive value US Medical PG Question 1: A 36-year-old female presents to clinic inquiring about the meaning of a previous negative test result from a new HIV screening test. The efficacy of this new screening test for HIV has been assessed by comparison against existing gold standard detection of HIV RNA via PCR. The study includes 1000 patients, with 850 HIV-negative patients (by PCR) receiving a negative test result, 30 HIV-negative patients receiving a positive test result, 100 HIV positive patients receiving a positive test result, and 20 HIV positive patients receiving a negative test result. Which of the following is most likely to increase the negative predictive value for this test?
- A. Decreased prevalence of HIV in the tested population (Correct Answer)
- B. Increased prevalence of HIV in the tested population
- C. Increased number of false positive test results
- D. Increased number of false negative test results
- E. Decreased number of false positive test results
Positive predictive value Explanation: ***Decreased prevalence of HIV in the tested population***
- A **lower prevalence** of a disease in the population means there are fewer actual cases, making a **negative test result** more reliable in ruling out the disease.
- This increases the probability that a person with a negative test truly does not have the disease, thus elevating the **negative predictive value (NPV)**.
*Increased prevalence of HIV in the tested population*
- A **higher prevalence** means there are more actual cases of HIV in the population.
- In this scenario, a negative test result is less reassuring, as there's a greater chance of missing a true positive case, leading to a **decreased NPV**.
*Increased number of false positive test results*
- **False positives** are instances where a test indicates disease when it's not present; they do not directly impact the ability of a negative test to predict absence of disease.
- While they affect the **positive predictive value (PPV)**, they do not directly alter the reliability of a negative result to exclude disease, so the NPV is not increased.
*Increased number of false negative test results*
- **False negatives** occur when a test indicates no disease, but the disease is actually present.
- An increase in false negatives directly implies that a negative test result is less trustworthy, leading to a **decrease in the NPV**.
*Decreased number of false positive test results*
- A decrease in false positive results primarily improves the **positive predictive value (PPV)**.
- While it indicates a more accurate test overall, it does not directly affect NPV, which measures the reliability of a negative test result in ruling out disease.
Positive predictive value US Medical PG Question 2: You are developing a new diagnostic test to identify patients with disease X. Of 100 patients tested with the gold standard test, 10% tested positive. Of those that tested positive, the experimental test was positive for 90% of those patients. The specificity of the experimental test is 20%. What is the positive predictive value of this new test?
- A. 10%
- B. 90%
- C. 95%
- D. 11% (Correct Answer)
- E. 20%
Positive predictive value Explanation: ***11%***
- The positive predictive value (PPV) is calculated as **true positives / (true positives + false positives)**.
- From 100 patients, 10 have disease (prevalence 10%). With 90% sensitivity, the test correctly identifies **9 true positives** (90% of 10).
- Of 90 patients without disease, specificity of 20% means 20% are correctly identified as negative (18 true negatives), so **72 false positives** = 90 × (1 - 0.20).
- Therefore, PPV = 9 / (9 + 72) = 9/81 = **11.1% ≈ 11%**.
*10%*
- This value represents the **prevalence** of the disease in the population, not the positive predictive value of the test.
- Prevalence is the proportion of individuals who have the disease (10 out of 100 patients).
*90%*
- This figure represents the **sensitivity** of the test, which is the percentage of true positives correctly identified by the experimental test.
- Sensitivity = true positives / (true positives + false negatives) = 9/10 = 90%.
*95%*
- This value is not directly derivable from the given data and does not represent any standard test characteristic in this context.
- It would imply a much higher PPV than what can be calculated given the low specificity of 20%.
*20%*
- This is the stated **specificity** of the test, which measures the proportion of true negatives correctly identified.
- Specificity = true negatives / (true negatives + false positives) = 18/90 = 20%.
Positive predictive value US Medical PG Question 3: A 27-year-old man interested in pre-exposure therapy for HIV (PrEP) is being evaluated to qualify for a PrEP study. In order to qualify, patients must be HIV- and hepatitis B- and C-negative. Any other sexually transmitted infections require treatment prior to initiation of PrEP. The medical history is positive for a prior syphilis infection and bipolar affective disorder, for which he takes lithium. On his next visit, the liver and renal enzymes are within normal ranges. HIV and hepatitis B and C tests are negative. Which of the following about the HIV test is true?
- A. It is a quantitative test used for screening purposes.
- B. It is a qualitative test used for screening purposes. (Correct Answer)
- C. A secondary reagent is needed to interpret the results.
- D. A known antigen binds directly to the patient's serum.
- E. An unknown antigen binds to the known serum.
Positive predictive value Explanation: ***It is a qualitative test used for screening purposes.***
- **HIV screening tests** (e.g., 4th generation antibody/antigen combination assays) are typically **qualitative**, meaning they detect the presence or absence of HIV markers, not their exact amount.
- These tests are primarily used for broad **screening** of populations to identify potential cases of HIV infection.
*It is a quantitative test used for screening purposes.*
- **Quantitative tests** for HIV, such as viral load tests, measure the amount of virus in the blood and are typically used for monitoring disease progression or treatment effectiveness, not for initial screening.
- Screening tests are designed for high sensitivity to detect infection, even with low viral loads or early antibody responses, making a quantitative measurement less relevant for initial screening.
*A secondary reagent is needed to interpret the results.*
- While some complex immunoassays might involve multiple steps, modern **HIV screening tests** often use advanced technologies that directly yield results, making a separate secondary reagent for interpretation generally unnecessary.
- The results are typically indicated by a color change or a signal detected by an instrument, without requiring an additional interpretive reagent.
*A known antigen binds directly to the patient's serum.*
- **HIV antibody tests** detect **antibodies** produced by the patient's immune system in response to HIV infection.
- In such tests, **known HIV antigens** (from the test kit) bind to **HIV-specific antibodies present in the patient's serum**, not to serum components directly.
- This option is incorrect because it omits the critical role of antibodies as the target molecules being detected.
*An unknown antigen binds to the known serum.*
- This statement describes a different type of immunological assay where an unknown antigen is being identified using a known antibody, which is contrary to how **HIV screening tests** for infection are typically structured.
- **HIV screening tests** use known components (e.g., HIV antigens or antibodies) in the test kit to detect unknown components (e.g., HIV antibodies or viral antigens) in the patient's sample.
Positive predictive value US Medical PG Question 4: A novel PET radiotracer is being evaluated for its ability to aid in the diagnosis of Alzheimer’s disease (AD). The study decides to use a sample size of 1,000 patients, and half of the patients enrolled have AD. In the group of patients with AD, 400 are found positive on the novel type of PET imaging examination. In the control group, 50 are found positive. What is the PPV of this novel exam?
- A. 400 / (400+50) (Correct Answer)
- B. 450 / (450 + 100)
- C. 400 / (400+100)
- D. 450 / (450 + 50)
- E. 400 / (400 + 150)
Positive predictive value Explanation: ***400 / (400+50)***
- The **Positive Predictive Value (PPV)** is the probability that subjects with a positive test result actually have the disease. It's calculated as **True Positives / (True Positives + False Positives)**.
- In this scenario, **True Positives** are 400 (patients with AD who tested positive), and **False Positives** are 50 (control patients without AD who tested positive).
*450 / (450 + 100)*
- This calculation incorrectly includes **False Negatives** (450, total AD patients - true positives) in the numerator or denominator for PPV, and misidentifies other components.
- The formula for PPV specifically focuses on positive test results and the proportion of those that are truly disease-positive.
*400 / (400+100)*
- This option correctly identifies **True Positives** as 400 but incorrectly assumes **False Positives** are 100.
- The problem states that 50 control patients (without AD) tested positive, which are the false positives.
*450 / (450 + 50)*
- This formula incorrectly uses **450** as the number of **True Positives**, which represents the total number of patients with AD testing positive and negative (400 TP + 100 FN).
- PPV only considers those who tested positive in its numerator.
*400 / (400 + 150)*
- While 400 is correctly identified as **True Positives**, the **False Positives** are incorrectly stated as 150.
- The problem explicitly states that 50 control patients were found positive, making 50 the correct number for false positives.
Positive predictive value US Medical PG Question 5: A medical research study is beginning to evaluate the positive predictive value of a novel blood test for non-Hodgkin’s lymphoma. The diagnostic arm contains 700 patients with NHL, of which 400 tested positive for the novel blood test. In the control arm, 700 age-matched control patients are enrolled and 0 are found positive for the novel test. What is the PPV of this test?
- A. 400 / (400 + 0) (Correct Answer)
- B. 700 / (700 + 300)
- C. 400 / (400 + 300)
- D. 700 / (700 + 0)
- E. 700 / (400 + 400)
Positive predictive value Explanation: ***400 / (400 + 0) = 1.0 or 100%***
- The **positive predictive value (PPV)** is calculated as **True Positives / (True Positives + False Positives)**.
- In this scenario, **True Positives (TP)** are the 400 patients with NHL who tested positive, and **False Positives (FP)** are 0, as no control patients tested positive.
- This gives a PPV of 400/400 = **1.0 or 100%**, indicating that all patients who tested positive actually had the disease.
*700 / (700 + 300)*
- This calculation does not align with the formula for PPV based on the given data.
- The denominator `(700+300)` suggests an incorrect combination of various patient groups.
*400 / (400 + 300)*
- The denominator `(400+300)` incorrectly includes 300, which is the number of **False Negatives** (patients with NHL who tested negative), not False Positives.
- PPV focuses on the proportion of true positives among all positive tests, not all diseased individuals.
*700 / (700 + 0)*
- This calculation incorrectly uses the total number of patients with NHL (700) as the numerator, rather than the number of positive test results in that group.
- The numerator should be the **True Positives** (400), not the total number of diseased individuals.
*700 / (400 + 400)*
- This calculation uses incorrect values for both the numerator and denominator, not corresponding to the PPV formula.
- The numerator 700 represents the total number of patients with the disease, not those who tested positive, and the denominator incorrectly sums up values that don't represent the proper PPV calculation.
Positive predictive value US Medical PG Question 6: A pharmaceutical corporation is developing a research study to evaluate a novel blood test to screen for breast cancer. They enrolled 800 patients in the study, half of which have breast cancer. The remaining enrolled patients are age-matched controls who do not have the disease. Of those in the diseased arm, 330 are found positive for the test. Of the patients in the control arm, only 30 are found positive. What is this test’s sensitivity?
- A. 330 / (330 + 30)
- B. 330 / (330 + 70) (Correct Answer)
- C. 370 / (30 + 370)
- D. 370 / (70 + 370)
- E. 330 / (400 + 400)
Positive predictive value Explanation: ***330 / (330 + 70)***
- **Sensitivity** measures the proportion of actual **positives** that are correctly identified as such.
- In this study, there are **400 diseased patients** (half of 800). Of these, 330 tested positive (true positives), meaning 70 tested negative (false negatives). So sensitivity is **330 / (330 + 70)**.
*330 / (330 + 30)*
- This calculation represents the **positive predictive value**, which is the probability that subjects with a positive screening test truly have the disease. It uses **true positives / (true positives + false positives)**.
- It does not correctly calculate **sensitivity**, which requires knowing the total number of diseased individuals.
*370 / (30 + 370)*
- This expression is attempting to calculate **specificity**, which is the proportion of actual negatives that are correctly identified. It would be **true negatives / (true negatives + false positives)**.
- However, the numbers used are incorrect for specificity in this context given the data provided.
*370 / (70 + 370)*
- This formula is an incorrect combination of values and does not represent any standard epidemiological measure like **sensitivity** or **specificity**.
- It is attempting to combine false negatives (70) and true negatives (370 from control arm) in a non-standard way.
*330 / (400 + 400)*
- This calculation attempts to divide true positives by the total study population (800 patients).
- This metric represents the **prevalence of true positives within the entire study cohort**, not the test's **sensitivity**.
Positive predictive value US Medical PG Question 7: A public health campaign increases vaccination rates against human papillomaviruses 16 and 18. Increased vaccination rates would have which of the following effects on the Papanicolaou test?
- A. Decreased true positive rate
- B. Decreased positive predictive value (Correct Answer)
- C. Decreased negative predictive value
- D. Increased positive likelihood ratio
- E. Increased true negative rate
Positive predictive value Explanation: ***Decreased positive predictive value***
- An increase in vaccination rates against **HPV 16 and 18** will reduce the **prevalence of cervical dysplasia and cancer** caused by these types.
- With fewer true cases in the population, a Papanicolaou (Pap) test is more likely to yield a **false positive result** when it tests positive, thus decreasing its **positive predictive value**.
- **PPV = TP/(TP+FP)** - when disease prevalence decreases, the number of true positives decreases while false positives remain relatively stable, reducing the overall PPV.
*Decreased true positive rate*
- The **true positive rate (sensitivity)** of the Pap test refers to its ability to correctly identify individuals with the disease (cervical dysplasia/cancer).
- While the overall number of true positives will decrease due to reduced disease prevalence, the inherent ability of the test to detect existing disease (i.e., its sensitivity) is **not directly affected by vaccination rates**.
- Sensitivity is an intrinsic test property: **Sensitivity = TP/(TP+FN)**.
*Decreased negative predictive value*
- The **negative predictive value** is the probability that a person with a negative test result truly does not have the disease.
- As the prevalence of the disease decreases due to vaccination, the probability of a negative test being truly negative actually **increases**, leading to an **increased negative predictive value**.
- **NPV = TN/(TN+FN)** - lower prevalence means fewer false negatives relative to true negatives.
*Increased positive likelihood ratio*
- The **positive likelihood ratio** describes how much more likely a positive test result is in someone with the disease compared to someone without the disease and is derived from sensitivity and specificity.
- **LR+ = Sensitivity/(1-Specificity)** - vaccination reduces disease prevalence but does not inherently change the **diagnostic accuracy** (sensitivity and specificity) of the Pap test, so the likelihood ratio remains unchanged.
*Increased true negative rate*
- The **true negative rate (specificity)** of the Pap test refers to its ability to correctly identify individuals who do not have the disease.
- While the overall number of true negatives will increase (because there are fewer cases to begin with), the inherent ability of the test to correctly identify healthy individuals (i.e., its specificity) is **not directly affected by the change in disease prevalence**.
- Specificity is an intrinsic test property: **Specificity = TN/(TN+FP)**.
Positive predictive value US Medical PG Question 8: A 65-year-old non-smoking woman with no symptoms comes to your clinic to establish care with a primary care provider. She hasn’t seen a doctor in 12 years and states that she feels very healthy. You realize that guidelines by the national cancer organization suggest that she is due for some cancer screening tests, including a mammogram for breast cancer, a colonoscopy for colon cancer, and a pap smear for cervical cancer. These three screening tests are most likely to be considered which of the following?
- A. Tertiary prevention
- B. Primary prevention
- C. Secondary prevention (Correct Answer)
- D. Cancer screening does not fit into these categories
- E. Quaternary prevention
Positive predictive value Explanation: ***Secondary prevention***
- **Secondary prevention** aims to detect and treat a disease early, before symptoms appear, to prevent its progression or recurrence.
- **Cancer screening tests** such as mammograms, colonoscopies, and Pap smears fit this category perfectly as they are performed in asymptomatic individuals to identify early-stage cancer or pre-cancerous lesions.
*Tertiary prevention*
- **Tertiary prevention** focuses on minimizing the impact of an established disease and improving quality of life through treatment and rehabilitation.
- This would involve managing existing cancer, not screening for it.
*Primary prevention*
- **Primary prevention** aims to prevent a disease from occurring in the first place, often through health promotion and risk reduction.
- Examples include vaccination, lifestyle modifications (e.g., healthy diet, exercise), or avoiding smoking.
*Cancer screening does not fit into these categories*
- This statement is incorrect as cancer screening is a well-established component of preventive healthcare.
- It clearly falls within the defined categories of prevention, specifically secondary prevention.
*Quaternary prevention*
- **Quaternary prevention** aims to protect patients from medical interventions that are likely to cause more harm than good, or to avoid over-medicalization.
- This concept is distinct from screening for diseases and focuses on ethical considerations in medical care.
Positive predictive value US Medical PG Question 9: A 50-year-old male presents to his primary care physician for a routine check-up. He reports that he is doing well overall without any bothersome symptoms. His past medical history is significant only for hypertension, which has been well controlled with losartan. Vital signs are as follows: T 37.0 C, HR 80, BP 128/76, RR 14, SpO2 99%. Physical examination does not reveal any concerning abnormalities. The physician recommends a fecal occult blood test at this visit to screen for the presence of any blood in the patient's stool that might be suggestive of an underlying colorectal cancer. Which of the following best describes this method of disease prevention?
- A. Primary prevention
- B. Primordial prevention
- C. Secondary prevention (Correct Answer)
- D. Tertiary prevention
- E. Quaternary prevention
Positive predictive value Explanation: ***Secondary prevention***
- **Secondary prevention** involves **early detection** of a disease or health problem in apparently healthy individuals. Screening tests, such as the fecal occult blood test used to detect colorectal cancer before symptoms arise, are prime examples of secondary prevention.
- The goal is to identify and address the disease in its early stages, allowing for timely intervention and potentially improving outcomes.
*Primary prevention*
- **Primary prevention** aims to **prevent a disease from occurring** in the first place by reducing risk factors or increasing protective factors. Examples include vaccinations, promoting healthy diets, and regular exercise.
- In this scenario, the individual is already being screened for a potential disease, not taking measures to prevent its initial development.
*Primordial prevention*
- **Primordial prevention** focuses on **preventing the development of risk factors** themselves at a societal level. This often involves public policy and environmental changes to promote healthier lifestyles.
- It targets broad determinants of health before specific risk factors emerge in individuals, which is distinct from an individual screening test.
*Tertiary prevention*
- **Tertiary prevention** occurs **after a disease has been diagnosed** and aims to prevent progression, reduce complications, improve quality of life, and restore function. Examples include rehabilitation after a stroke or chemotherapy for cancer.
- The patient in the scenario is asymptomatic and undergoing screening, not managing an existing, diagnosed condition.
*Quaternary prevention*
- **Quaternary prevention** aims to **protect patients from medical interventions** that are likely to cause more harm than good, or to mitigate the consequences of unnecessary or excessive medical care. It focuses on identifying and avoiding overmedicalization.
- The fecal occult blood test is a standard screening tool in this context, not an intervention designed to counter the negative effects of over-treatment.
Positive predictive value US Medical PG Question 10: You are reviewing raw data from a research study performed at your medical center examining the effectiveness of a novel AIDS screening examination. The study enrolled 250 patients with confirmed AIDS, and 240 of these patients demonstrated a positive screening examination. The control arm of the study enrolled 250 patients who do not have AIDS, and only 5 of these patients tested positive on the novel screening examination. What is the NPV of this novel test?
- A. 240 / (240 + 15)
- B. 240 / (240 + 5)
- C. 240 / (240 + 10)
- D. 245 / (245 + 10) (Correct Answer)
- E. 245 / (245 + 5)
Positive predictive value Explanation: ***245 / (245 + 10)***
- The **negative predictive value (NPV)** is calculated as **true negatives (TN)** divided by the sum of **true negatives (TN)** and **false negatives (FN)**.
- In this study, there are 250 patients with AIDS; 240 tested positive (true positives, TP), meaning 10 tested negative (false negatives, FN = 250 - 240). There are 250 patients without AIDS; 5 tested positive (false positives, FP), meaning 245 tested negative (true negatives, TN = 250 - 5). Therefore, NPV = 245 / (245 + 10).
*240 / (240 + 15)*
- This calculation incorrectly uses the number of **true positives** (240) in the numerator and denominator, which is relevant for **positive predictive value (PPV)**, not NPV.
- The denominator `(240 + 15)` does not correspond to a valid sum for calculating NPV from the given data.
*240 / (240 + 5)*
- This calculation incorrectly uses **true positives** (240) in the numerator, which is not part of the NPV formula.
- The denominator `(240 + 5)` mixes true positives and false positives, which is incorrect for NPV.
*240 / (240 + 10)*
- This incorrectly places **true positives** (240) in the numerator instead of **true negatives**.
- The denominator `(240+10)` represents **true positives + false negatives**, which is related to sensitivity, not NPV.
*245 / (245 + 5)*
- This calculation correctly identifies **true negatives** (245) in the numerator but incorrectly uses **false positives** (5) in the denominator instead of **false negatives**.
- The denominator for NPV should be **true negatives + false negatives**, which is 245 + 10.
More Positive predictive value US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.