Likelihood ratios US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Likelihood ratios. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Likelihood ratios US Medical PG Question 1: A researcher is trying to determine whether a newly discovered substance X can be useful in promoting wound healing after surgery. She conducts this study by enrolling the next 100 patients that will be undergoing this surgery and separating them into 2 groups. She decides which patient will be in which group by using a random number generator. Subsequently, she prepares 1 set of syringes with the novel substance X and 1 set of syringes with a saline control. Both of these sets of syringes are unlabeled and the substances inside cannot be distinguished. She gives the surgeon performing the surgery 1 of the syringes and does not inform him nor the patient which syringe was used. After the study is complete, she analyzes all the data that was collected and performs statistical analysis. This study most likely provides which level of evidence for use of substance X?
- A. Level 3
- B. Level 1 (Correct Answer)
- C. Level 4
- D. Level 5
- E. Level 2
Likelihood ratios Explanation: ***Level 1***
- The study design described is a **randomized controlled trial (RCT)**, which is considered the **highest level of evidence (Level 1)** in the hierarchy of medical evidence.
- Key features like **randomization**, **control group**, and **blinding (double-blind)** help minimize bias and strengthen the validity of the findings.
*Level 2*
- Level 2 evidence typically comprises **well-designed controlled trials without randomization** (non-randomized controlled trials) or **high-quality cohort studies**.
- While strong, they do not possess the same level of internal validity as randomized controlled trials.
*Level 3*
- Level 3 evidence typically includes **case-control studies** or **cohort studies**, which are observational designs and carry a higher risk of bias compared to RCTs.
- These studies generally do not involve randomization or intervention assignment by the researchers.
*Level 4*
- Level 4 evidence is usually derived from **case series** or **poor quality cohort and case-control studies**.
- These studies provide descriptive information or investigate associations without strong control for confounding factors.
*Level 5*
- Level 5 evidence is the **lowest level of evidence**, consisting of **expert opinion** or **animal research/bench research**.
- This level lacks human clinical data or systematic investigative rigor needed for higher evidence levels.
Likelihood ratios US Medical PG Question 2: A 26-year-old medical student comes to the physician with a 3-week history of night sweats and myalgias. During this time, he has also had a 3.6-kg (8-lb) weight loss. He returned from a 6-month tropical medicine rotation in Cambodia 1 month ago. A chest x-ray (CXR) shows reticulonodular opacities suggestive of active tuberculosis (TB). The student is curious about his likelihood of having active TB. He reads a study that compares sputum testing results between 2,800 patients with likely active TB on a basis of history, clinical symptoms, and CXR pattern and 2,400 controls. The results are shown:
Sputum testing positive for TB Sputum testing negative for TB Total
Active TB likely on basis of history, clinical symptoms, and CXR pattern 700 2100 2,800
Active TB not likely on basis of history, clinical symptoms, and CXR pattern 300 2100 2,400
Total 1000 4200 5,200
Which of the following values reflects the probability that a patient with a diagnosis of active TB on the basis of history, clinical symptoms, and CXR pattern actually has active TB?
- A. 1.4
- B. 0.50
- C. 0.70
- D. 0.88
- E. 0.25 (Correct Answer)
Likelihood ratios Explanation: ***0.25***
- This value represents the **positive predictive value (PPV)** for active TB based on the initial clinical assessment criteria (history, symptoms, CXR).
- PPV is calculated as the number of true positives (700) divided by the total number of individuals with a positive clinical diagnosis (700 + 2100 = 2800). So, 700 / 2800 = 0.25.
- **This answers the question**: the probability that someone with a clinical diagnosis of active TB actually has the disease.
*Incorrect 1.4*
- This value is not a valid probability, as probabilities must be between 0 and 1.0.
- It might arise from an incorrect calculation or misinterpretation of the provided data.
*Incorrect 0.50*
- This value does not correspond to any standard diagnostic metric calculated from the provided data.
- The actual prevalence of TB (based on positive sputum) is 1000/5200 = 0.19, not 0.50.
- This is likely a distractor with no meaningful interpretation in this context.
*Incorrect 0.70*
- This value represents the **sensitivity** of the sputum test for detecting active TB.
- Sensitivity is calculated as true positives (700) divided by total with disease (700 + 300 = 1000). So, 700 / 1000 = 0.70.
- Sensitivity tells us how good the test is at detecting disease when present, not the probability of having disease given a positive clinical diagnosis.
*Incorrect 0.88*
- This value represents the **specificity** of the clinical assessment.
- Specificity is calculated as true negatives (2100) divided by total without disease (2100 + 300 = 2400). So, 2100 / 2400 = 0.875 ≈ 0.88.
- Specificity tells us how good the assessment is at ruling out disease in those without it, not the probability of disease given a positive assessment.
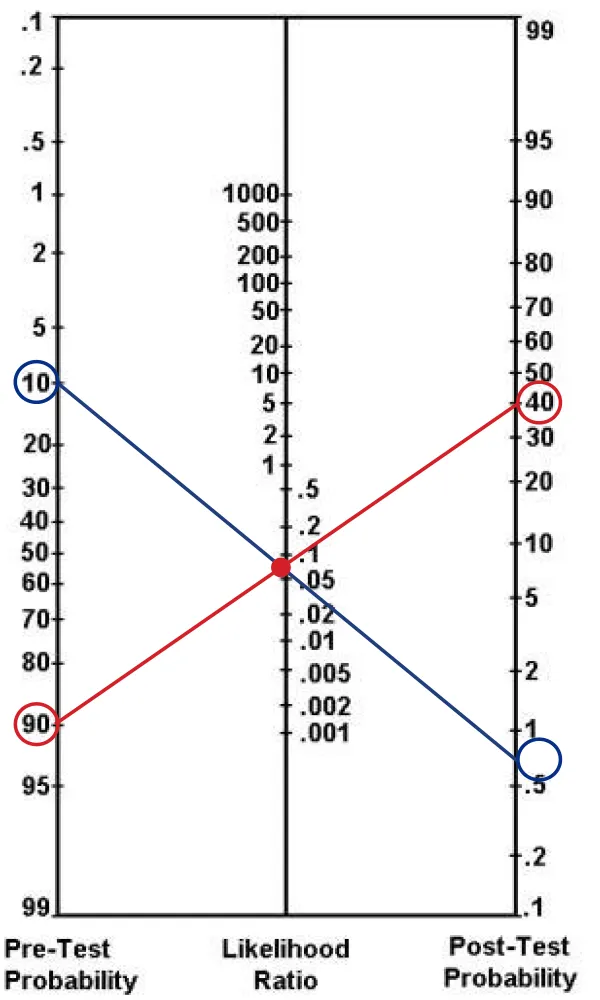
Likelihood ratios US Medical PG Question 3: A research group wants to assess the safety and toxicity profile of a new drug. A clinical trial is conducted with 20 volunteers to estimate the maximum tolerated dose and monitor the apparent toxicity of the drug. The study design is best described as which of the following phases of a clinical trial?
- A. Phase 0
- B. Phase III
- C. Phase V
- D. Phase II
- E. Phase I (Correct Answer)
Likelihood ratios Explanation: ***Phase I***
- **Phase I clinical trials** involve a small group of healthy volunteers (typically 20-100) to primarily assess **drug safety**, determine a safe dosage range, and identify side effects.
- The main goal is to establish the **maximum tolerated dose (MTD)** and evaluate the drug's pharmacokinetic and pharmacodynamic profiles.
*Phase 0*
- **Phase 0 trials** are exploratory studies conducted in a very small number of subjects (10-15) to gather preliminary data on a drug's **pharmacodynamics and pharmacokinetics** in humans.
- They involve microdoses, not intended to have therapeutic effects, and thus cannot determine toxicity or MTD.
*Phase III*
- **Phase III trials** are large-scale studies involving hundreds to thousands of patients to confirm the drug's **efficacy**, monitor side effects, compare it to standard treatments, and collect information that will allow the drug to be used safely.
- These trials are conducted after safety and initial efficacy have been established in earlier phases.
*Phase V*
- "Phase V" is not a standard, recognized phase in the traditional clinical trial classification (Phase 0, I, II, III, IV).
- This term might be used in some non-standard research contexts or for post-marketing studies that go beyond Phase IV surveillance, but it is not a formal phase for initial drug development.
*Phase II*
- **Phase II trials** involve several hundred patients with the condition the drug is intended to treat, focusing on **drug efficacy** and further evaluating safety.
- While safety is still monitored, the primary objective shifts to determining if the drug works for its intended purpose and at what dose.
Likelihood ratios US Medical PG Question 4: In 2013 the national mean score on the USMLE Step 1 exam was 227 with a standard deviation of 22. Assuming that the scores for 15,000 people follow a normal distribution, approximately how many students scored above the mean but below 250?
- A. 5,100 (Correct Answer)
- B. 4,500
- C. 6,000
- D. 3,750
- E. 6,750
Likelihood ratios Explanation: ***5,100***
- To solve this, first calculate the **z-score** for 250: (250 - 227) / 22 = 1.045.
- Using a **z-table**, the area under the curve from the mean (z=0) to z=1.045 is approximately 0.353. Multiplying this by 15,000 students gives approximately **5,295 students**, which is closest to 5,100.
*4,500*
- This answer would imply a smaller proportion of students between the mean and 250 (around 30%), which is lower than the calculated z-score of 1.045 suggests.
- It does not accurately reflect the area under the **normal distribution curve** for the given range.
*6,000*
- This option would mean that approximately 40% of students scored in this range, which would correspond to a z-score much higher than 1.045 or a different standard deviation.
- This calculation overestimates the number of students within the specified range.
*3,750*
- This value represents 25% of the total students (15,000 * 0.25), indicating that only a quarter of the distribution lies in this range.
- This significantly underestimates the proportion of students scoring between the mean and 250 for the given standard deviation.
*6,750*
- This option reflects approximately 45% of the total student population (15,000 * 0.45), which would correspond to a much larger z-score or a different distribution.
- This value is an overestimation and does not align with the standard normal distribution probabilities for the given parameters.
Likelihood ratios US Medical PG Question 5: You are reviewing raw data from a research study performed at your medical center examining the effectiveness of a novel AIDS screening examination. The study enrolled 250 patients with confirmed AIDS, and 240 of these patients demonstrated a positive screening examination. The control arm of the study enrolled 250 patients who do not have AIDS, and only 5 of these patients tested positive on the novel screening examination. What is the NPV of this novel test?
- A. 240 / (240 + 15)
- B. 240 / (240 + 5)
- C. 240 / (240 + 10)
- D. 245 / (245 + 10) (Correct Answer)
- E. 245 / (245 + 5)
Likelihood ratios Explanation: ***245 / (245 + 10)***
- The **negative predictive value (NPV)** is calculated as **true negatives (TN)** divided by the sum of **true negatives (TN)** and **false negatives (FN)**.
- In this study, there are 250 patients with AIDS; 240 tested positive (true positives, TP), meaning 10 tested negative (false negatives, FN = 250 - 240). There are 250 patients without AIDS; 5 tested positive (false positives, FP), meaning 245 tested negative (true negatives, TN = 250 - 5). Therefore, NPV = 245 / (245 + 10).
*240 / (240 + 15)*
- This calculation incorrectly uses the number of **true positives** (240) in the numerator and denominator, which is relevant for **positive predictive value (PPV)**, not NPV.
- The denominator `(240 + 15)` does not correspond to a valid sum for calculating NPV from the given data.
*240 / (240 + 5)*
- This calculation incorrectly uses **true positives** (240) in the numerator, which is not part of the NPV formula.
- The denominator `(240 + 5)` mixes true positives and false positives, which is incorrect for NPV.
*240 / (240 + 10)*
- This incorrectly places **true positives** (240) in the numerator instead of **true negatives**.
- The denominator `(240+10)` represents **true positives + false negatives**, which is related to sensitivity, not NPV.
*245 / (245 + 5)*
- This calculation correctly identifies **true negatives** (245) in the numerator but incorrectly uses **false positives** (5) in the denominator instead of **false negatives**.
- The denominator for NPV should be **true negatives + false negatives**, which is 245 + 10.
Likelihood ratios US Medical PG Question 6: A 45-year-old man presents for his annual checkup. The patient has a past medical history of diabetes mellitus (DM) type 2 that is well-controlled with diet. In addition, he was admitted to this hospital 1-year ago for a myocardial infarction (MI). The patient reports a 40-pack-year smoking history. However, after his MI, his doctors informed him about how detrimental smoking was to his heart condition. Since then, he has made efforts to cut down and now, for the past seven months, has stopped smoking. He says he used to use smoking as a means of dealing with his work and family stresses. He now attends wellness sessions at work and meditates early every morning before the family wakes up. Which of the following stages of the transtheoretical model is this patient most likely in?
- A. Preparation
- B. Contemplation
- C. Action
- D. Precontemplation
- E. Maintenance (Correct Answer)
Likelihood ratios Explanation: ***Maintenance***
- The patient has **successfully stopped smoking for seven months**, indicating sustained behavior change.
- He has also adopted **new coping mechanisms** like wellness sessions and meditation, which are crucial for preventing relapse and falls under this stage.
*Preparation*
- This stage involves **intending to take action** in the immediate future (e.g., within the next month) and involves some steps towards change, such as making a plan.
- The patient has already acted and sustained the behavior change, moving past mere preparation.
*Contemplation*
- Individuals in this stage are **aware a problem exists** and are seriously thinking about overcoming it but have not yet committed to taking action.
- The patient has clearly moved past just thinking about quitting and has actively stopped smoking.
*Action*
- This stage involves **modifying behavior, experiences, or environment** in order to overcome problems.
- While the patient was in the action stage when he initially quit, he has now maintained this change for an extended period (seven months), progressing beyond the initial action phase.
*Precontemplation*
- In this stage, individuals are **not intending to take action** in the foreseeable future (e.g., within 6 months) and are often unaware or underaware of their problems.
- This patient actively quit smoking and maintained cessation, showing he was not in precontemplation.
Likelihood ratios US Medical PG Question 7: A 7-year-old girl presents for a follow-up visit after recent discharge from the hospital. She was admitted about 4 months ago for symptoms of seizures, altered mental status, and fever. She was diagnosed during that admission with herpes encephalitis and recovered well after being treated with acyclovir. However, at this visit, her parents complain of some “strange behaviors” that have developed over the past several weeks. For example, she seems to be snacking uncontrollably and eats significantly more than she did before. Her teacher has also sent home notes stating that she has been chewing on art supplies such as crayons and glue and that she has been sent to the principal twice for rubbing her genitals inappropriately during class. The pediatric neurologist decides to get a follow-up MRI. Which of the following parts of the brain is most likely to have abnormal findings?
- A. Amygdala (Correct Answer)
- B. Hippocampus
- C. Brainstem
- D. Lateral geniculate nucleus
- E. Substantia nigra
Likelihood ratios Explanation: ***Amygdala***
- Herpes encephalitis commonly affects the **temporal lobes**, which house the amygdala, leading to **Klüver-Bucy syndrome** symptoms like hyperorality, hypersexuality, and hyperphagia.
- The described "strange behaviors" (uncontrolled snacking, chewing non-food items, inappropriate genital rubbing) are classic manifestations of **Klüver-Bucy syndrome**, which results from bilateral damage to the amygdala.
*Hippocampus*
- While the hippocampus is also located in the temporal lobe and can be affected by herpes encephalitis, damage primarily leads to **memory deficits** (anterograde amnesia).
- It is not directly responsible for the behavioral changes seen in Klüver-Bucy syndrome.
*Brainstem*
- The brainstem controls **vital functions** (e.g., breathing, heart rate) and consciousness.
- Damage to the brainstem would present with more severe and acute symptoms, such as **coma**, respiratory failure, or cranial nerve palsies, not the specific behavioral disturbances observed.
*Lateral geniculate nucleus*
- The lateral geniculate nucleus is a relay center for **visual information** in the thalamus.
- Damage would primarily result in **visual field defects** or problems with visual processing, not the behavioral changes described.
*Substantia nigra*
- Located in the midbrain, the substantia nigra is crucial for **motor control** due to its role in dopamine production.
- Damage is classically associated with **Parkinsonian symptoms** (e.g., tremor, rigidity, bradykinesia), which are not present in this patient.
Likelihood ratios US Medical PG Question 8: A pharmaceutical company develops a sequential testing protocol for a rare genetic disorder (prevalence 0.01%). Initial screening test has sensitivity 95% and specificity 90%. Positive results undergo confirmatory testing with sensitivity 99% and specificity 99.5%. The company claims this approach achieves PPV >80% for the final positive result. Evaluate this claim and the rationale for sequential testing in this context.
- A. The claim is true; sequential testing increases PPV by enriching the population tested in the second step (Correct Answer)
- B. The claim is false; sensitivity decreases with sequential testing, reducing PPV
- C. Sequential testing is unnecessary; the first test alone achieves adequate PPV
- D. The claim is false; sequential testing cannot achieve PPV >80% with such low prevalence
- E. The claim is true; the high specificity of the confirmatory test ensures high PPV regardless of prevalence
Likelihood ratios Explanation: ***The claim is true; sequential testing increases PPV by enriching the population tested in the second step***
- Sequential testing works by increasing the **pre-test probability** for the second test, as the cohort being tested has already screened positive once.
- By applying a highly specific confirmatory test to this enriched group, the number of **false positives** is significantly reduced, which drastically improves the **Positive Predictive Value (PPV)**.
*The claim is false; sequential testing cannot achieve PPV >80% with such low prevalence*
- Even with a low **prevalence**, the multiplication of specificities in a sequential process can reduce the **False Positive** rate to a level where the PPV exceeds 80%.
- This line of reasoning ignores that the **denominator** of the PPV calculation (True Positives + False Positives) decreases much faster than the numerator during the second stage.
*The claim is true; the high specificity of the confirmatory test ensures high PPV regardless of prevalence*
- While high **specificity** is crucial, PPV is always dependent on the **prevalence** (pre-test probability) of the condition in the group being tested.
- The claim is true because sequential testing specifically raises that **pre-test probability**, not because prevalence is irrelevant to the calculation.
*The claim is false; sensitivity decreases with sequential testing, reducing PPV*
- It is true that **net sensitivity** decreases in sequential testing, but a decrease in sensitivity actually tends to have a negligible effect on PPV compared to specificity gains.
- **PPV** is primarily driven by the **specificity** and the prevalence in the tested population, both of which are optimized in this two-step protocol.
*Sequential testing is unnecessary; the first test alone achieves adequate PPV*
- Given a prevalence of 0.01% and 90% specificity, the **first test** alone would yield a massive amount of false positives, resulting in a very low PPV (~0.09%).
- A **confirmatory test** is clinically and ethically necessary to avoid wrongly diagnosing thousands of healthy individuals with a **rare genetic disorder**.
Likelihood ratios US Medical PG Question 9: A hospital system is implementing a sepsis screening algorithm using clinical criteria with sensitivity of 92% and specificity of 75%. False positives result in unnecessary antibiotics, cultures, and ICU evaluations costing $3,000 per case. Missing true sepsis cases (false negatives) results in average increased mortality and morbidity costs of $50,000 per case. Hospital sepsis prevalence is 8%. Evaluate the optimal threshold adjustment strategy.
- A. Maintain current threshold as it balances sensitivity and specificity equally
- B. Implement risk stratification with different thresholds for different populations
- C. Abandon screening due to unacceptable false positive rate
- D. Increase threshold to improve specificity and reduce costs from false positives
- E. Decrease threshold to improve sensitivity despite more false positives (Correct Answer)
Likelihood ratios Explanation: ***Decrease threshold to improve sensitivity despite more false positives***
- In sepsis screening, the **cost of a false negative** ($50,000) is nearly 17 times higher than the **cost of a false positive** ($3,000), necessitating a strategy that prioritizes **sensitivity** to minimize missed cases.
- Lowering the threshold further ensures fewer high-cost **mortality and morbidity** events occur, which is the most economically and clinically sound approach given the significant **weighted cost** of missing a diagnosis.
*Increase threshold to improve specificity and reduce costs from false positives*
- Increasing the threshold would increase the number of **false negatives**, leading to massive financial losses due to the $50,000 cost per missed **sepsis case**.
- While it reduces the $3,000 expense of unnecessary **antibiotics and cultures**, the savings are mathematically dwarfed by the increased costs of untreated sepsis.
*Maintain current threshold as it balances sensitivity and specificity equally*
- A balanced threshold is inappropriate when the **consequences of error types** are highly asymmetrical; the algorithm should favor the side with the more severe outcome.
- Simply balancing **sensitivity and specificity** fails to account for the 8% **prevalence** and the extreme disparity in costs between false positives and false negatives.
*Implement risk stratification with different thresholds for different populations*
- While risk stratification is useful, it does not address the fundamental need to minimize **false negatives** across the entire 8% prevalence population.
- This approach adds **operational complexity** without necessarily solving the primary economic imbalance between **screening costs** and mortality costs.
*Abandon screening due to unacceptable false positive rate*
- Abandoning screening would lead to an even higher rate of **missed sepsis cases**, resulting in catastrophic clinical outcomes and **increased hospital liability**.
- The current 75% **specificity** is acceptable because the clinical priority in sepsis is **early detection** to prevent rapid physiological deterioration.
Likelihood ratios US Medical PG Question 10: A 58-year-old man with chronic cough undergoes evaluation for tuberculosis. A tuberculin skin test (TST) is positive (15mm induration). TST has sensitivity of 80% and specificity of 95% in immunocompetent adults. However, he received BCG vaccination as a child in Asia. Local TB prevalence is 0.5%, but his occupational exposure increases his pre-test probability to 10%. Evaluate the most appropriate interpretation and management approach.
- A. Calculate post-test probability and obtain interferon-gamma release assay (IGRA) (Correct Answer)
- B. Repeat TST in 2 weeks to confirm
- C. Treat empirically regardless of test characteristics
- D. Positive test confirms TB; start treatment immediately
- E. False positive due to BCG; no further testing needed
Likelihood ratios Explanation: ***Calculate post-test probability and obtain interferon-gamma release assay (IGRA)***
- In individuals previously vaccinated with **BCG**, the **Tuberculin Skin Test (TST)** can yield **false positives** because the test cross-reacts with BCG antigens, whereas **IGRA** is more specific.
- Clinical decision-making requires integrating **pre-test probability** (10% in this case) with test characteristics to determine **post-test probability** before starting long-term therapy.
*Positive test confirms TB; start treatment immediately*
- A positive **TST** in a patient with a **BCG vaccination** history does not automatically confirm infection; it lacks the specificity to distinguish between vaccination and actual **Mycobacterium tuberculosis** infection.
- Starting **antitubercular therapy** immediately without ruling out a false positive or assessing for **active versus latent disease** violates standard diagnostic protocols.
*False positive due to BCG; no further testing needed*
- While **BCG** causes false positives, the patient’s **occupational exposure** and a significant **15mm induration** make infection plausible; dismissing the result is unsafe.
- High-risk individuals require definitive testing, usually via **IGRA**, to ensure **latent tuberculosis infection (LTBI)** is not overlooked.
*Repeat TST in 2 weeks to confirm*
- Repeating a **TST** within a short window can lead to the **booster effect**, where the second test appears positive due to immunological memory rather than new infection.
- Re-testing with the same diagnostic tool does not solve the underlying issue of **BCG cross-reactivity**; a different, more specific test is required.
*Treat empirically regardless of test characteristics*
- Empirical treatment ignores the potential for **medication toxicity** (e.g., hepatotoxicity from Isoniazid) in a patient who might not actually have **LTBI**.
- Evidence-based medicine requires utilizing **sensitivity, specificity, and prevalence** to justify treatment, especially when more specific tests like **IGRA** are available.
More Likelihood ratios US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.
