Type I and Type II errors US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Type I and Type II errors. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Type I and Type II errors US Medical PG Question 1: A randomized double-blind controlled trial is conducted on the efficacy of 2 different ACE-inhibitors. The null hypothesis is that both drugs will be equivalent in their blood-pressure-lowering abilities. The study concluded, however, that Medication 1 was more efficacious in lowering blood pressure than medication 2 as determined by a p-value < 0.01 (with significance defined as p ≤ 0.05). Which of the following statements is correct?
- A. We can accept the null hypothesis.
- B. We can reject the null hypothesis. (Correct Answer)
- C. This trial did not reach statistical significance.
- D. There is a 0.1% chance that medication 2 is superior.
- E. There is a 10% chance that medication 1 is superior.
Type I and Type II errors Explanation: ***We can reject the null hypothesis.***
- A **p-value < 0.01** indicates that the observed difference is **statistically significant** at the **α = 0.05 level**, meaning there is strong evidence against the null hypothesis.
- When a result is statistically significant (p < α), we **reject the null hypothesis**. This is the standard statistical terminology for concluding that the observed effect is unlikely to be due to chance alone.
*We can accept the null hypothesis.*
- A **p-value < 0.01** is **less than the significance level of 0.05**, providing strong evidence to **reject the null hypothesis**, not accept it.
- Accepting the null hypothesis would imply there's no treatment effect, which contradicts the study's finding that Medication 1 was more efficacious.
- Note: In hypothesis testing, we never truly "accept" the null hypothesis; we either reject it or fail to reject it.
*This trial did not reach statistical significance.*
- The trial **did reach statistical significance** because the **p-value (p < 0.01) is less than the defined significance level (p ≤ 0.05)**.
- A p-value of 0.01 indicates a 1% chance that the observed results occurred by random chance if the null hypothesis were true.
*There is a 0.1% chance that medication 2 is superior.*
- The p-value of **p < 0.01** relates to the probability of observing the data (or more extreme data) given the null hypothesis is true, not the probability of one medication being superior.
- It does not directly provide the probability of Medication 2 being superior; rather, it indicates the **unlikelihood of the observed difference** if no true difference exists.
*There is a 10% chance that medication 1 is superior.*
- A **p-value of < 0.01** means there is **less than a 1% chance** of observing such a result if the null hypothesis (no difference) were true, not a 10% chance of superiority.
- The p-value represents the probability of observing the data, or more extreme data, assuming the **null hypothesis is true**, not the probability that one treatment is superior.
Type I and Type II errors US Medical PG Question 2: A 25-year-old man with a genetic disorder presents for genetic counseling because he is concerned about the risk that any children he has will have the same disease as himself. Specifically, since childhood he has had difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy. He has also had diarrhea and malabsorption requiring enzyme replacement therapy. If his wife comes from a population where 1 in 10,000 people are affected by this same disorder, which of the following best represents the likelihood a child would be affected as well?
- A. 0.01%
- B. 2%
- C. 0.5%
- D. 1% (Correct Answer)
- E. 50%
Type I and Type II errors Explanation: ***Correct Option: 1%***
- The patient's symptoms (difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy; diarrhea and malabsorption requiring enzyme replacement therapy) are classic for **cystic fibrosis (CF)**, an **autosomal recessive disorder**.
- For an autosomal recessive disorder with a prevalence of 1 in 10,000 in the general population, **q² = 1/10,000**, so **q = 1/100 = 0.01**. The carrier frequency **(2pq)** is approximately **2q = 2 × (1/100) = 1/50 = 0.02**.
- The affected man is **homozygous recessive (aa)** and will always pass on the recessive allele. His wife has a **1/50 chance of being a carrier (Aa)**. If she is a carrier, she has a **1/2 chance of passing on the recessive allele**.
- Therefore, the probability of an affected child = **(Probability wife is a carrier) × (Probability wife passes recessive allele) = 1/50 × 1/2 = 1/100 = 1%**.
*Incorrect Option: 0.01%*
- This percentage is too low and does not correctly account for the carrier frequency in the population and the probability of transmission from a carrier mother.
*Incorrect Option: 2%*
- This represents approximately the carrier frequency (1/50 ≈ 2%), but does not account for the additional 1/2 probability that a carrier mother would pass on the recessive allele.
*Incorrect Option: 0.5%*
- This value would be correct if the carrier frequency were 1/100 instead of 1/50, which does not match the given population prevalence.
*Incorrect Option: 50%*
- **50%** would be the risk if both parents were carriers of an autosomal recessive disorder (1/4 chance = 25% for affected, but if we know one parent passes the allele, conditional probability changes). More accurately, 50% would apply if the disorder were **autosomal dominant** with one affected parent, which is not the case here.
Type I and Type II errors US Medical PG Question 3: A research group wants to assess the safety and toxicity profile of a new drug. A clinical trial is conducted with 20 volunteers to estimate the maximum tolerated dose and monitor the apparent toxicity of the drug. The study design is best described as which of the following phases of a clinical trial?
- A. Phase 0
- B. Phase III
- C. Phase V
- D. Phase II
- E. Phase I (Correct Answer)
Type I and Type II errors Explanation: ***Phase I***
- **Phase I clinical trials** involve a small group of healthy volunteers (typically 20-100) to primarily assess **drug safety**, determine a safe dosage range, and identify side effects.
- The main goal is to establish the **maximum tolerated dose (MTD)** and evaluate the drug's pharmacokinetic and pharmacodynamic profiles.
*Phase 0*
- **Phase 0 trials** are exploratory studies conducted in a very small number of subjects (10-15) to gather preliminary data on a drug's **pharmacodynamics and pharmacokinetics** in humans.
- They involve microdoses, not intended to have therapeutic effects, and thus cannot determine toxicity or MTD.
*Phase III*
- **Phase III trials** are large-scale studies involving hundreds to thousands of patients to confirm the drug's **efficacy**, monitor side effects, compare it to standard treatments, and collect information that will allow the drug to be used safely.
- These trials are conducted after safety and initial efficacy have been established in earlier phases.
*Phase V*
- "Phase V" is not a standard, recognized phase in the traditional clinical trial classification (Phase 0, I, II, III, IV).
- This term might be used in some non-standard research contexts or for post-marketing studies that go beyond Phase IV surveillance, but it is not a formal phase for initial drug development.
*Phase II*
- **Phase II trials** involve several hundred patients with the condition the drug is intended to treat, focusing on **drug efficacy** and further evaluating safety.
- While safety is still monitored, the primary objective shifts to determining if the drug works for its intended purpose and at what dose.
Type I and Type II errors US Medical PG Question 4: A medical research study is beginning to evaluate the positive predictive value of a novel blood test for non-Hodgkin’s lymphoma. The diagnostic arm contains 700 patients with NHL, of which 400 tested positive for the novel blood test. In the control arm, 700 age-matched control patients are enrolled and 0 are found positive for the novel test. What is the PPV of this test?
- A. 400 / (400 + 0) (Correct Answer)
- B. 700 / (700 + 300)
- C. 400 / (400 + 300)
- D. 700 / (700 + 0)
- E. 700 / (400 + 400)
Type I and Type II errors Explanation: ***400 / (400 + 0) = 1.0 or 100%***
- The **positive predictive value (PPV)** is calculated as **True Positives / (True Positives + False Positives)**.
- In this scenario, **True Positives (TP)** are the 400 patients with NHL who tested positive, and **False Positives (FP)** are 0, as no control patients tested positive.
- This gives a PPV of 400/400 = **1.0 or 100%**, indicating that all patients who tested positive actually had the disease.
*700 / (700 + 300)*
- This calculation does not align with the formula for PPV based on the given data.
- The denominator `(700+300)` suggests an incorrect combination of various patient groups.
*400 / (400 + 300)*
- The denominator `(400+300)` incorrectly includes 300, which is the number of **False Negatives** (patients with NHL who tested negative), not False Positives.
- PPV focuses on the proportion of true positives among all positive tests, not all diseased individuals.
*700 / (700 + 0)*
- This calculation incorrectly uses the total number of patients with NHL (700) as the numerator, rather than the number of positive test results in that group.
- The numerator should be the **True Positives** (400), not the total number of diseased individuals.
*700 / (400 + 400)*
- This calculation uses incorrect values for both the numerator and denominator, not corresponding to the PPV formula.
- The numerator 700 represents the total number of patients with the disease, not those who tested positive, and the denominator incorrectly sums up values that don't represent the proper PPV calculation.
Type I and Type II errors US Medical PG Question 5: An academic medical center in the United States is approached by a pharmaceutical company to run a small clinical trial to test the effectiveness of its new drug, compound X. The company wants to know if the measured hemoglobin a1c (Hba1c) of patients with type 2 diabetes receiving metformin and compound X would be lower than that of control subjects receiving only metformin. After a year of study and data analysis, researchers conclude that the control and treatment groups did not differ significantly in their Hba1c levels.
However, parallel clinical trials in several other countries found that compound X led to a significant decrease in Hba1c. Interested in the discrepancy between these findings, the company funded a larger study in the United States, which confirmed that compound X decreased Hba1c levels. After compound X was approved by the FDA, and after several years of use in the general population, outcomes data confirmed that it effectively lowered Hba1c levels and increased overall survival. What term best describes the discrepant findings in the initial clinical trial run by institution A?
- A. Type I error
- B. Hawthorne effect
- C. Type II error (Correct Answer)
- D. Publication bias
- E. Confirmation bias
Type I and Type II errors Explanation: ***Type II error***
- A **Type II error** occurs when a study fails to **reject a false null hypothesis**, meaning it concludes there is no significant difference or effect when one actually exists.
- In this case, the initial US trial incorrectly concluded that Compound X had no significant effect on HbA1c, while subsequent larger studies and real-world data proved it did.
*Type I error*
- A **Type I error** (alpha error) occurs when a study incorrectly **rejects a true null hypothesis**, concluding there is a significant difference or effect when there isn't.
- This scenario describes the opposite: the initial study failed to find an effect that genuinely existed, indicating a Type II error, not a Type I error.
*Hawthorne effect*
- The **Hawthorne effect** is a type of reactivity in which individuals modify an aspect of their behavior in response to their awareness of being observed.
- This effect does not explain the initial trial's failure to detect a real drug effect; rather, it relates to participants changing behavior due to study participation itself.
*Publication bias*
- **Publication bias** occurs when studies with positive or statistically significant results are more likely to be published than those with negative or non-significant results.
- While relevant to the literature as a whole, it doesn't explain the discrepancy in findings within a single drug's development where a real effect was initially missed.
*Confirmation bias*
- **Confirmation bias** is the tendency to search for, interpret, favor, and recall information in a way that confirms one's preexisting beliefs or hypotheses.
- This bias would likely lead researchers to *find* an effect if they expected one, or to disregard data that contradicts their beliefs, which is not what happened in the initial trial.
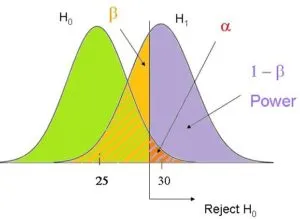
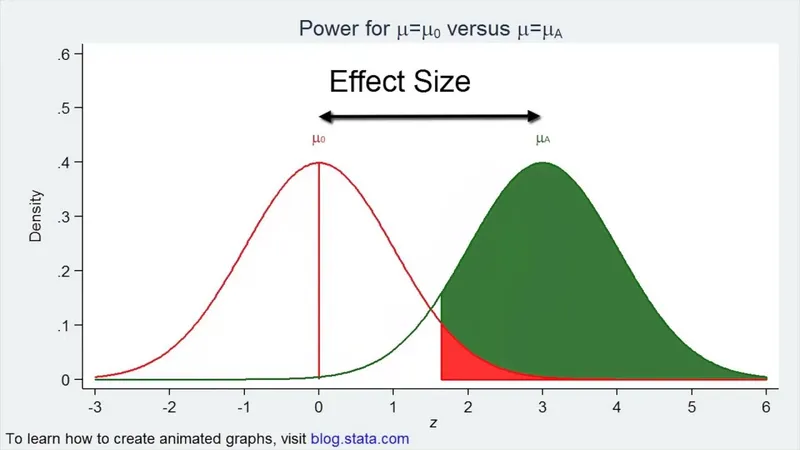
Type I and Type II errors US Medical PG Question 6: The height of American adults is expected to follow a normal distribution, with a typical male adult having an average height of 69 inches with a standard deviation of 0.1 inches. An investigator has been informed about a community in the American Midwest with a history of heavy air and water pollution in which a lower mean height has been reported. The investigator plans to sample 30 male residents to test the claim that heights in this town differ significantly from the national average based on heights assumed be normally distributed. The significance level is set at 10% and the probability of a type 2 error is assumed to be 15%. Based on this information, which of the following is the power of the proposed study?
- A. 0.10
- B. 0.85 (Correct Answer)
- C. 0.90
- D. 0.15
- E. 0.05
Type I and Type II errors Explanation: ***0.85***
- **Power** is defined as **1 - β**, where β is the **probability of a Type II error**.
- Given that the probability of a **Type II error (β)** is 15% or 0.15, the power of the study is 1 - 0.15 = **0.85**.
*0.10*
- This value represents the **significance level (α)**, which is the probability of committing a **Type I error** (rejecting a true null hypothesis).
- The significance level is distinct from the **power of the study**, which relates to Type II errors.
*0.90*
- This value would be the power if the **Type II error rate (β)** was 0.10 (1 - 0.10 = 0.90), but the question specifies a β of 0.15.
- It is also the complement of the significance level (1 - α), which is not the definition of power.
*0.15*
- This value is the **probability of a Type II error (β)**, not the power of the study.
- **Power** is the probability of correctly rejecting a false null hypothesis, which is 1 - β.
*0.05*
- While 0.05 is a common significance level (α), it is not given as the significance level in this question (which is 0.10).
- This value also does not represent the power of the study, which would be calculated using the **Type II error rate**.
Type I and Type II errors US Medical PG Question 7: A 55-year-old man with recurrent pneumonia comes to the physician for a follow-up examination one week after hospitalization for pneumonia. He feels well but still has a productive cough. He has smoked 1 pack of cigarettes daily for 5 years. His temperature is 36.9°C (98.4°F) and respirations are 20/min. Cardiopulmonary examination shows coarse crackles at the right lung base. Microscopic examination of a biopsy specimen of the right lower lung parenchyma shows proliferation of clustered, cuboidal, foamy-appearing cells. These cells are responsible for which of the following functions?
- A. Mucus secretion
- B. Cytokine release
- C. Lecithin production (Correct Answer)
- D. Toxin degradation
- E. Gas diffusion
Type I and Type II errors Explanation: ***Lecithin production***
- The description of **clustered, cuboidal, foamy-appearing cells** in the lung parenchyma strongly suggests **Type II pneumocytes**.
- **Type II pneumocytes** are primarily responsible for producing and secreting **pulmonary surfactant**, which is rich in **lecithin (phosphatidylcholine)**, to reduce surface tension in the alveoli.
*Mucus secretion*
- **Goblet cells** and **submucosal glands** in the airways are responsible for mucus secretion, not the alveolar cells described.
- Mucus functions to trap particles and pathogens, preventing them from reaching the alveoli.
*Cytokine release*
- While various lung cells, including macrophages and epithelial cells, can release cytokines in response to inflammation or infection, it is not the primary defining function of Type II pneumocytes.
- **Cytokine release** is a broad immune response, not specific to the unique morphology and function described.
*Toxin degradation*
- The liver and kidneys are the primary organs for **toxin degradation** and excretion, though some detoxification can occur in the lungs.
- This function is not characteristic of **Type II pneumocytes**, which are focused on surfactant production and alveolar repair.
*Gas diffusion*
- **Gas diffusion** primarily occurs across the **Type I pneumocytes** (squamous alveolar cells) and the capillary endothelial cells due to their thinness and large surface area.
- **Type II pneumocytes** are thicker and less involved in direct gas exchange.
Type I and Type II errors US Medical PG Question 8: An 18-year-old male reports to his physician that he is having repeated episodes of a "racing heart beat". He believes these episodes are occurring completely at random. He is experiencing approximately 2 episodes each week, each lasting for only a few minutes. During the episodes he feels palpitations and shortness of breath, then nervous and uncomfortable, but these feelings resolve in a matter of minutes. He is otherwise well. Vital signs are as follows: T 98.8F, HR 60 bpm, BP 110/80 mmHg, RR 12. His resting EKG shows a short PR interval and a delta wave. What is the likely diagnosis?
- A. Atrioventricular reentrant tachycardia (Correct Answer)
- B. Paroxysmal atrial fibrillation
- C. Ventricular tachycardia
- D. Panic attacks
- E. Atrioventricular block, Mobitz Type II
Type I and Type II errors Explanation: ***Atrioventricular reentrant tachycardia***
- The patient's presentation with sudden onset, paroxysmal episodes of "racing heartbeat," shortness of breath, and nervousness in an otherwise healthy young male is highly suggestive of **supraventricular tachycardia (SVT)**.
- The **short PR interval and delta wave** on resting EKG are pathognomonic for **Wolff-Parkinson-White (WPW) syndrome**, which involves an accessory pathway (bundle of Kent) between the atria and ventricles.
- **Atrioventricular reentrant tachycardia (AVRT)** is the most common arrhythmia associated with WPW syndrome, where the reentrant circuit involves the accessory pathway, causing paroxysmal tachycardia episodes.
*Paroxysmal atrial fibrillation*
- While paroxysmal atrial fibrillation can cause a "racing heartbeat," it typically presents with an **irregularly irregular rhythm**, which is not suggested by the consistent episodes described.
- The presence of **delta waves on EKG** points specifically to an accessory pathway (WPW), not atrial fibrillation as the primary diagnosis.
- Note: Patients with WPW can develop atrial fibrillation, but it would conduct irregularly, not as the regular paroxysmal episodes described.
*Ventricular tachycardia*
- **Ventricular tachycardia (VT)** is a more serious arrhythmia, generally associated with structural heart disease or channelopathies, and typically presents with more severe symptoms like syncope or hemodynamic compromise.
- The **delta wave and short PR interval** indicate a supraventricular accessory pathway, not a ventricular origin of the arrhythmia.
- In a young, otherwise healthy individual with normal vital signs between episodes, VT is much less likely than AVRT.
*Panic attacks*
- While panic attacks can cause symptoms like palpitations and shortness of breath, they would not produce **EKG findings of delta waves and short PR interval**.
- The specific EKG findings indicate a **structural cardiac accessory pathway** rather than a purely psychological etiology.
- The description of consistent "racing heart beat" episodes with characteristic EKG changes confirms a primary cardiac arrhythmia (AVRT) rather than panic disorder.
*Atrioventricular block, Mobitz Type II*
- **Mobitz Type II AV block** is a bradyarrhythmia characterized by intermittent dropped QRS complexes following P waves, leading to a slow heart rate.
- This condition would cause **bradycardia and possible syncope**, not a "racing heart beat" or palpitations associated with tachycardia.
- The EKG findings of **short PR interval (not prolonged) and delta wave** are completely inconsistent with AV block.
Type I and Type II errors US Medical PG Question 9: An 18-month-old girl is brought to the pediatrician’s office for failure to thrive and developmental delay. The patient’s mother says she has not started speaking and is just now starting to pull herself up to standing position. Furthermore, her movement appears to be restricted. Physical examination reveals coarse facial features and restricted joint mobility. Laboratory studies show increased plasma levels of several enzymes. Which of the following is the underlying biochemical defect in this patient?
- A. Congenital lack of lysosomal formation
- B. Inappropriate protein targeting to endoplasmic reticulum
- C. Failure of mannose phosphorylation (Correct Answer)
- D. Inappropriate degradation of lysosomal enzymes
- E. Misfolding of nuclear proteins
Type I and Type II errors Explanation: ***Failure of mannose phosphorylation***
- The constellation of **failure to thrive**, **developmental delay**, **coarse facial features**, restricted joint mobility, and elevated plasma enzymes in an 18-month-old girl is highly suggestive of **I-cell disease** (mucolipidosis type II).
- **I-cell disease** is caused by the deficiency of **N-acetylglucosaminyl-1-phosphotransferase**, an enzyme responsible for phosphorylating mannose residues on lysosomal enzymes, which is crucial for proper targeting to the lysosome.
*Congenital lack of lysosomal formation*
- **Lysosomes** are present in this condition, but their enzymes are misdirected.
- A congenital lack of lysosomal formation would present with even more severe and widespread cellular dysfunction, possibly incompatible with life beyond early embryonic stages.
*Inappropriate protein targeting to endoplasmic reticulum*
- Proteins destined for the endoplasmic reticulum (ER) are typically targeted by an N-terminal signal peptide and then processed within the ER.
- While ER dysfunction can cause various disorders, the specific symptoms and enzyme elevations point away from a primary ER targeting defect related to lysosomal enzymes.
*Inappropriate degradation of lysosomal enzymes*
- In I-cell disease, lysosomal enzymes are synthesized but are **not properly targeted to the lysosomes**; instead, they are secreted into the bloodstream, leading to their elevated plasma levels.
- While some degradation might occur, the primary issue is mis-packaging and secretion, not increased degradation within the cell.
*Misfolding of nuclear proteins*
- Misfolding of nuclear proteins can lead to a variety of genetic disorders and cellular stress responses, but the clinical presentation, particularly the accumulation of undegraded material and elevated plasma lysosomal enzymes, is not characteristic of primary nuclear protein misfolding.
- The pathology in I-cell disease centers on lysosomal dysfunction rather than nuclear protein abnormalities.
Type I and Type II errors US Medical PG Question 10: A 52-year-old man presents for a routine checkup. Past medical history is remarkable for stage 1 systemic hypertension and hepatitis A infection diagnosed 10 years ago. He takes aspirin, rosuvastatin, enalapril daily, and a magnesium supplement every once in a while. He is planning to visit Ecuador for a week-long vacation and is concerned about malaria prophylaxis before his travel. The physician advised taking 1 primaquine pill every day while he is there and for 7 consecutive days after leaving Ecuador. On the third day of his trip, the patient develops an acute onset headache, dizziness, shortness of breath, and fingertips and toes turning blue. His blood pressure is 135/80 mm Hg, heart rate is 94/min, respiratory rate is 22/min, temperature is 36.9℃ (98.4℉), and blood oxygen saturation is 97% in room air. While drawing blood for his laboratory workup, the nurse notes that his blood has a chocolate brown color. Which of the following statements best describes the etiology of this patient’s most likely condition?
- A. The patient’s condition is due to consumption of water polluted with nitrates.
- B. The patient had pre-existing liver damage caused by viral hepatitis.
- C. This condition resulted from primaquine overdose.
- D. It is a type B adverse drug reaction. (Correct Answer)
- E. The condition developed because of his concomitant use of primaquine and magnesium supplement.
Type I and Type II errors Explanation: ***It is a type B adverse drug reaction.***
- The patient's symptoms (headache, dizziness, shortness of breath, cyanosis, chocolate brown blood) are consistent with **methemoglobinemia**, which is a known idiosyncratic reaction to **primaquine**. Type B adverse drug reactions are **unpredictable** and not dose-dependent, representing an individual's unique response to a drug.
- This reaction likely stems from an underlying **glucose-6-phosphate dehydrogenase (G6PD) deficiency**, making him susceptible to oxidative stress induced by primaquine, leading to methemoglobin formation. The occurrence of symptoms early in the course of medication (3rd day) also supports an idiosyncratic reaction rather than a typical dose-related effect.
*The patient’s condition is due to consumption of water polluted with nitrates.*
- While **nitrate poisoning** can cause methemoglobinemia, the patient’s symptoms appeared shortly after starting primaquine for malaria prophylaxis, making drug-induced methemoglobinemia a more direct and probable cause in this clinical context.
- Exposure to nitrate-polluted water is unlikely to cause a sudden onset of such severe symptoms within 3 days of arrival, especially considering he is taking a known oxidizing agent (primaquine).
*The patient had pre-existing liver damage caused by viral hepatitis.*
- Although **liver dysfunction** can alter drug metabolism, hepatitis A is an acute infection that does not typically cause chronic liver damage leading to altered drug metabolism for primaquine in the long term, especially 10 years after diagnosis.
- The primary risk factor for primaquine-induced methemoglobinemia is G6PD deficiency, not liver damage, which affects red blood cell susceptibility to oxidative stress.
*This condition resulted from primaquine overdose.*
- The prescribed dose of primaquine (one pill daily) is standard for malaria prophylaxis, and there is no indication the patient took more than prescribed. This reaction is likely due to an **idiosyncratic response** rather than an excessive dose.
- Methemoglobinemia from primaquine is often seen in individuals with **G6PD deficiency** even at therapeutic doses, making it an unpredictable Type B adverse reaction rather than a direct dose-dependent toxicity.
*The condition developed because of his concomitant use of primaquine and magnesium supplement.*
- There is no known direct significant **drug interaction** between primaquine and magnesium supplements that would lead to methemoglobinemia.
- The underlying cause of methemoglobinemia with primaquine is typically due to its **oxidative properties** in susceptible individuals (e.g., G6PD deficiency), not an interaction with magnesium.
More Type I and Type II errors US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.