P-values and confidence intervals US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for P-values and confidence intervals. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
P-values and confidence intervals US Medical PG Question 1: Group of 100 medical students took an end of the year exam. The mean score on the exam was 70%, with a standard deviation of 25%. The professor states that a student's score must be within the 95% confidence interval of the mean to pass the exam. Which of the following is the minimum score a student can have to pass the exam?
- A. 45%
- B. 63.75%
- C. 67.5%
- D. 20%
- E. 65% (Correct Answer)
P-values and confidence intervals Explanation: ***65%***
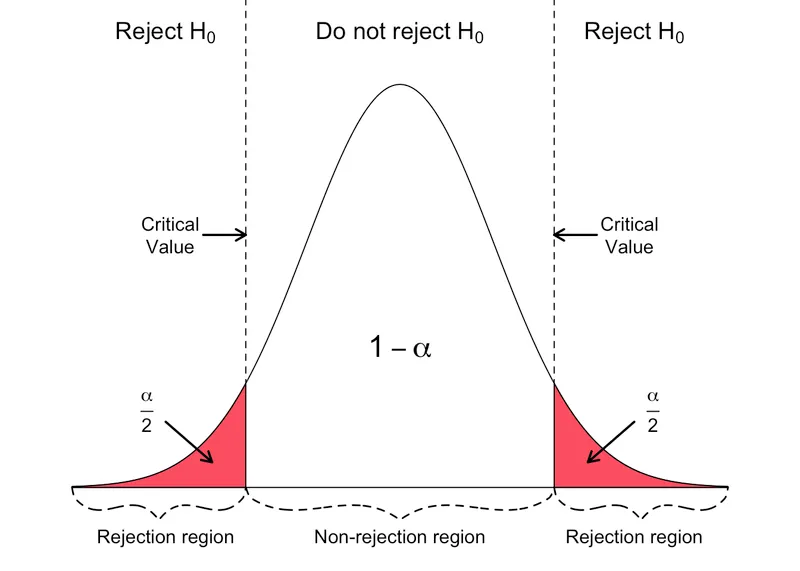
- To find the **95% confidence interval (CI) of the mean**, we use the formula: Mean ± (Z-score × Standard Error). For a 95% CI, the Z-score is approximately **1.96**.
- The **Standard Error (SE)** is calculated as SD/√n, where n is the sample size (100 students). So, SE = 25%/√100 = 25%/10 = **2.5%**.
- The 95% CI is 70% ± (1.96 × 2.5%) = 70% ± 4.9%. The lower bound is 70% - 4.9% = **65.1%**, which rounds to **65%** as the minimum passing score.
*45%*
- This value is significantly lower than the calculated lower bound of the 95% confidence interval (approximately 65.1%).
- It would represent a score far outside the defined passing range.
*63.75%*
- This value falls below the calculated lower bound of the 95% confidence interval (approximately 65.1%).
- While close, this score would not meet the professor's criterion for passing.
*67.5%*
- This value is within the 95% confidence interval (65.1% to 74.9%) but is **not the minimum score**.
- Lower scores within the interval would still qualify as passing.
*20%*
- This score is extremely low and falls significantly outside the 95% confidence interval for a mean of 70%.
- It would indicate performance far below the defined passing threshold.
P-values and confidence intervals US Medical PG Question 2: A 25-year-old man with a genetic disorder presents for genetic counseling because he is concerned about the risk that any children he has will have the same disease as himself. Specifically, since childhood he has had difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy. He has also had diarrhea and malabsorption requiring enzyme replacement therapy. If his wife comes from a population where 1 in 10,000 people are affected by this same disorder, which of the following best represents the likelihood a child would be affected as well?
- A. 0.01%
- B. 2%
- C. 0.5%
- D. 1% (Correct Answer)
- E. 50%
P-values and confidence intervals Explanation: ***Correct Option: 1%***
- The patient's symptoms (difficulty breathing requiring bronchodilators, inhaled corticosteroids, and chest physiotherapy; diarrhea and malabsorption requiring enzyme replacement therapy) are classic for **cystic fibrosis (CF)**, an **autosomal recessive disorder**.
- For an autosomal recessive disorder with a prevalence of 1 in 10,000 in the general population, **q² = 1/10,000**, so **q = 1/100 = 0.01**. The carrier frequency **(2pq)** is approximately **2q = 2 × (1/100) = 1/50 = 0.02**.
- The affected man is **homozygous recessive (aa)** and will always pass on the recessive allele. His wife has a **1/50 chance of being a carrier (Aa)**. If she is a carrier, she has a **1/2 chance of passing on the recessive allele**.
- Therefore, the probability of an affected child = **(Probability wife is a carrier) × (Probability wife passes recessive allele) = 1/50 × 1/2 = 1/100 = 1%**.
*Incorrect Option: 0.01%*
- This percentage is too low and does not correctly account for the carrier frequency in the population and the probability of transmission from a carrier mother.
*Incorrect Option: 2%*
- This represents approximately the carrier frequency (1/50 ≈ 2%), but does not account for the additional 1/2 probability that a carrier mother would pass on the recessive allele.
*Incorrect Option: 0.5%*
- This value would be correct if the carrier frequency were 1/100 instead of 1/50, which does not match the given population prevalence.
*Incorrect Option: 50%*
- **50%** would be the risk if both parents were carriers of an autosomal recessive disorder (1/4 chance = 25% for affected, but if we know one parent passes the allele, conditional probability changes). More accurately, 50% would apply if the disorder were **autosomal dominant** with one affected parent, which is not the case here.
P-values and confidence intervals US Medical PG Question 3: You are reading through a recent article that reports significant decreases in all-cause mortality for patients with malignant melanoma following treatment with a novel biological infusion. Which of the following choices refers to the probability that a study will find a statistically significant difference when one truly does exist?
- A. Type II error
- B. Type I error
- C. Confidence interval
- D. p-value
- E. Power (Correct Answer)
P-values and confidence intervals Explanation: ***Power***
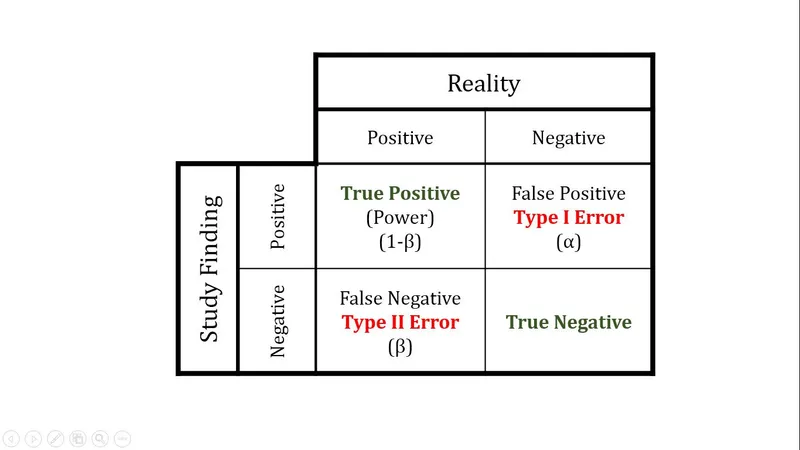
- **Power** is the probability that a study will correctly reject the null hypothesis when it is, in fact, false (i.e., will find a statistically significant difference when one truly exists).
- A study with high power minimizes the risk of a **Type II error** (failing to detect a real effect).
*Type II error*
- A **Type II error** (or **beta error**) occurs when a study fails to reject a false null hypothesis, meaning it concludes there is no significant difference when one actually exists.
- This is the **opposite** of what the question describes, which asks for the probability of *finding* a difference.
*Type I error*
- A **Type I error** (or **alpha error**) occurs when a study incorrectly rejects a true null hypothesis, concluding there is a significant difference when one does not actually exist.
- This relates to the **p-value** and the level of statistical significance (e.g., p < 0.05).
*Confidence interval*
- A **confidence interval** provides a range of values within which the true population parameter is likely to lie with a certain degree of confidence (e.g., 95%).
- It does not directly represent the probability of finding a statistically significant difference when one truly exists.
*p-value*
- The **p-value** is the probability of observing data as extreme as, or more extreme than, that obtained in the study, assuming the null hypothesis is true.
- It is used to determine statistical significance, but it is not the probability of detecting a true effect.
P-values and confidence intervals US Medical PG Question 4: A research group wants to assess the safety and toxicity profile of a new drug. A clinical trial is conducted with 20 volunteers to estimate the maximum tolerated dose and monitor the apparent toxicity of the drug. The study design is best described as which of the following phases of a clinical trial?
- A. Phase 0
- B. Phase III
- C. Phase V
- D. Phase II
- E. Phase I (Correct Answer)
P-values and confidence intervals Explanation: ***Phase I***
- **Phase I clinical trials** involve a small group of healthy volunteers (typically 20-100) to primarily assess **drug safety**, determine a safe dosage range, and identify side effects.
- The main goal is to establish the **maximum tolerated dose (MTD)** and evaluate the drug's pharmacokinetic and pharmacodynamic profiles.
*Phase 0*
- **Phase 0 trials** are exploratory studies conducted in a very small number of subjects (10-15) to gather preliminary data on a drug's **pharmacodynamics and pharmacokinetics** in humans.
- They involve microdoses, not intended to have therapeutic effects, and thus cannot determine toxicity or MTD.
*Phase III*
- **Phase III trials** are large-scale studies involving hundreds to thousands of patients to confirm the drug's **efficacy**, monitor side effects, compare it to standard treatments, and collect information that will allow the drug to be used safely.
- These trials are conducted after safety and initial efficacy have been established in earlier phases.
*Phase V*
- "Phase V" is not a standard, recognized phase in the traditional clinical trial classification (Phase 0, I, II, III, IV).
- This term might be used in some non-standard research contexts or for post-marketing studies that go beyond Phase IV surveillance, but it is not a formal phase for initial drug development.
*Phase II*
- **Phase II trials** involve several hundred patients with the condition the drug is intended to treat, focusing on **drug efficacy** and further evaluating safety.
- While safety is still monitored, the primary objective shifts to determining if the drug works for its intended purpose and at what dose.
P-values and confidence intervals US Medical PG Question 5: An academic medical center in the United States is approached by a pharmaceutical company to run a small clinical trial to test the effectiveness of its new drug, compound X. The company wants to know if the measured hemoglobin a1c (Hba1c) of patients with type 2 diabetes receiving metformin and compound X would be lower than that of control subjects receiving only metformin. After a year of study and data analysis, researchers conclude that the control and treatment groups did not differ significantly in their Hba1c levels.
However, parallel clinical trials in several other countries found that compound X led to a significant decrease in Hba1c. Interested in the discrepancy between these findings, the company funded a larger study in the United States, which confirmed that compound X decreased Hba1c levels. After compound X was approved by the FDA, and after several years of use in the general population, outcomes data confirmed that it effectively lowered Hba1c levels and increased overall survival. What term best describes the discrepant findings in the initial clinical trial run by institution A?
- A. Type I error
- B. Hawthorne effect
- C. Type II error (Correct Answer)
- D. Publication bias
- E. Confirmation bias
P-values and confidence intervals Explanation: ***Type II error***
- A **Type II error** occurs when a study fails to **reject a false null hypothesis**, meaning it concludes there is no significant difference or effect when one actually exists.
- In this case, the initial US trial incorrectly concluded that Compound X had no significant effect on HbA1c, while subsequent larger studies and real-world data proved it did.
*Type I error*
- A **Type I error** (alpha error) occurs when a study incorrectly **rejects a true null hypothesis**, concluding there is a significant difference or effect when there isn't.
- This scenario describes the opposite: the initial study failed to find an effect that genuinely existed, indicating a Type II error, not a Type I error.
*Hawthorne effect*
- The **Hawthorne effect** is a type of reactivity in which individuals modify an aspect of their behavior in response to their awareness of being observed.
- This effect does not explain the initial trial's failure to detect a real drug effect; rather, it relates to participants changing behavior due to study participation itself.
*Publication bias*
- **Publication bias** occurs when studies with positive or statistically significant results are more likely to be published than those with negative or non-significant results.
- While relevant to the literature as a whole, it doesn't explain the discrepancy in findings within a single drug's development where a real effect was initially missed.
*Confirmation bias*
- **Confirmation bias** is the tendency to search for, interpret, favor, and recall information in a way that confirms one's preexisting beliefs or hypotheses.
- This bias would likely lead researchers to *find* an effect if they expected one, or to disregard data that contradicts their beliefs, which is not what happened in the initial trial.
P-values and confidence intervals US Medical PG Question 6: You submit a paper to a prestigious journal about the effects of coffee consumption on mesothelioma risk. The first reviewer lauds your clinical and scientific acumen, but expresses concern that your study does not have adequate statistical power. Statistical power refers to which of the following?
- A. The probability of detecting an association when no association exists.
- B. The probability of not detecting an association when an association does exist.
- C. The probability of detecting an association when an association does exist. (Correct Answer)
- D. The first derivative of work.
- E. The square root of the variance.
P-values and confidence intervals Explanation: ***The probability of detecting an association when an association does exist.***
- **Statistical power** is defined as the probability that a study will correctly reject a false null hypothesis, meaning it will detect a true effect or association if one exists.
- A study with **adequate statistical power** is less likely to miss a real effect.
*The probability of detecting an association when no association exists.*
- This describes a **Type I error** or **false positive**, often represented by **alpha (α)**.
- It is the probability of incorrectly concluding an effect or association exists when, in reality, there is none.
*The probability of not detecting an association when an association does exist.*
- This refers to a **Type II error** or **false negative**, represented by **beta (β)**.
- **Statistical power** is calculated as **1 - β**, so this option describes the complement of power.
*The first derivative of work.*
- The first derivative of work with respect to time represents **power** in physics, which is the rate at which work is done.
- This option is a **distractor** from physics and is unrelated to statistical power in research.
*The square root of the variance.*
- The **square root of the variance** is the **standard deviation**, a measure of the dispersion or spread of data.
- This is a statistical concept but is not the definition of statistical power.
P-values and confidence intervals US Medical PG Question 7: A prospective cohort study was conducted to assess the relationship between LDL and the incidence of heart disease. The patients were selected at random. Results showed a 10-year relative risk of 2.3 for people with elevated LDL levels compared to individuals with normal LDL levels. The 95% confidence interval was 1.05-3.50. This study is most likely to have which of the following p values?
- A. 0.20
- B. 0.06
- C. 0.08
- D. 0.04 (Correct Answer)
- E. 0.10
P-values and confidence intervals Explanation: ***0.04***
- A 95% confidence interval that **does not include 1 (one)** suggests a **statistically significant** association, meaning the p-value is likely to be **less than 0.05**.
- The given CI of 1.05-3.50 for the relative risk (RR) is entirely above 1, indicating a significant positive association, and therefore, a p-value less than 0.05.
*0.20*
- A p-value of 0.20 is **greater than 0.05**, which would imply the finding is **not statistically significant**.
- If the p-value were 0.20, the 95% confidence interval would likely **include 1**, suggesting no significant difference in risk.
*0.06*
- A p-value of 0.06 is **greater than 0.05**, indicating that the association is **not statistically significant at the conventional alpha level**.
- If the p-value were 0.06, the 95% confidence interval would likely **include 1**, or be very close to including it, contradicting the given CI of 1.05-3.50.
*0.08*
- A p-value of 0.08 is **greater than 0.05**, indicating that the finding is **not statistically significant**.
- If the p-value were 0.08, the 95% confidence interval would almost certainly **include 1**, which is inconsistent with the provided interval.
*0.10*
- A p-value of 0.10 is **greater than 0.05**, which signifies that the finding is **not statistically significant**.
- If the p-value were 0.10, the 95% confidence interval for the relative risk would typically **include 1**, contradicting the given confidence interval.
P-values and confidence intervals US Medical PG Question 8: A researcher is investigating the effects of a new antihypertensive medication on renal physiology. She gives a subject a dose of the new medication, and she then collects plasma and urine samples. She finds the following: Hematocrit: 40%; Serum creatinine: 0.0125 mg/mL; Urine creatinine: 1.25 mg/mL. Urinary output is 1 mL/min. Renal blood flow is 1 L/min. Based on the above information and approximating that the creatinine clearance is equal to the GFR, what answer best approximates filtration fraction in this case?
- A. 10%
- B. 17% (Correct Answer)
- C. 33%
- D. 50%
- E. 25%
P-values and confidence intervals Explanation: ***17%***
- First, calculate **GFR** using the creatinine clearance formula: GFR = (Urine creatinine × Urinary output) / Serum creatinine = (1.25 mg/mL × 1 mL/min) / 0.0125 mg/mL = **100 mL/min**.
- Next, calculate **Renal Plasma Flow (RPF)** from Renal Blood Flow (RBF) and Hematocrit: RPF = RBF × (1 - Hematocrit) = 1000 mL/min × (1 - 0.40) = **600 mL/min**.
- Finally, calculate **Filtration Fraction (FF)** = GFR / RPF = 100 mL/min / 600 mL/min = 0.1667 = **16.7%, which approximates to 17%**.
- This is the correct answer based on the physiological calculations and represents a normal filtration fraction.
*10%*
- This would correspond to a filtration fraction of 0.10, which would require either a GFR of 60 mL/min (lower than calculated) or an RPF of 1000 mL/min (higher than calculated).
- This value is too low given the provided parameters and doesn't match the calculation from the given data.
*25%*
- This value would suggest FF = 0.25, requiring a GFR of 150 mL/min with the calculated RPF of 600 mL/min.
- This is higher than the calculated GFR of 100 mL/min and doesn't match the given creatinine values.
*33%*
- This would imply FF = 0.33, requiring a GFR of approximately 200 mL/min with RPF of 600 mL/min.
- This is significantly higher than the calculated GFR and would represent an abnormally elevated filtration fraction.
*50%*
- A filtration fraction of 50% is unphysiologically high and would indicate severe pathology.
- This would require a GFR of 300 mL/min with the calculated RPF, which is impossible given the provided creatinine clearance data.
P-values and confidence intervals US Medical PG Question 9: A child is learning the steps of hand hygiene. Which domain of learning is primarily involved?
- A. Cognitive
- B. Affective
- C. Psychomotor (Correct Answer)
- D. Affective & cognitive
- E. Cognitive & Psychomotor
P-values and confidence intervals Explanation: ***Psychomotor***
- The **psychomotor domain** involves the acquisition of skills that require coordination of mental and physical activities, such as performing a physical task like hand hygiene.
- This domain focuses on the ability to carry out **physical movements** with precision and coordination.
*Cognitive*
- The **cognitive domain** primarily deals with intellectual understanding, knowledge, and problem-solving, which would involve understanding *why* hand hygiene is important, not the physical act itself.
- While essential for appreciating the *rationale* behind the steps, it does not encompass the *execution* of the skill.
*Affective*
- The **affective domain** relates to emotions, attitudes, values, and appreciation for the task, such as a child's **willingness to perform hand hygiene**.
- It involves feelings and motivations rather than the physical or intellectual mastery of a skill.
*Affective & cognitive*
- While both affective (motivation, willingness) and cognitive (understanding the importance) domains play a supportive role, neither directly addresses the **physical execution** of the learned steps.
- The primary domain for *learning the steps* (i.e., actually performing the actions) is psychomotor.
*Cognitive & Psychomotor*
- While both cognitive (understanding) and psychomotor (physical execution) domains are involved in the overall learning process, the question specifically asks about **learning the steps**, which primarily emphasizes the **psychomotor** aspect.
- The cognitive component is foundational but secondary to the actual motor skill acquisition being described.
P-values and confidence intervals US Medical PG Question 10: A 46-year-old man comes to the physician for a follow-up evaluation one week after being discharged from the hospital for acute pancreatitis and alcohol withdrawal. He drinks 8 to 10 beers daily. When the physician asks him about his alcohol use, the patient says, “This is the second time in a year that I have experienced such severe belly pain because of my pancreas. I realize that it really could be happening because of the amount of alcohol I am drinking. However, I don't think I have the willpower to cut down.” This patient is most likely in which of the following stages of behavioral change?
- A. Action
- B. Precontemplation
- C. Preparation
- D. Maintenance
- E. Contemplation (Correct Answer)
P-values and confidence intervals Explanation: ***Contemplation***
- The patient **acknowledges** the problem ("realize that it really could be happening because of the amount of alcohol I am drinking") and considers the link between his behavior and health issues.
- He expresses an intent to change but also feelings of **ambivalence** or a lack of willpower ("I don't think I have the willpower to cut down"), which are hallmarks of this stage.
*Action*
- This stage involves **actively modifying behavior**, environment, or experiences to overcome the problem.
- The patient has not yet taken concrete steps to cut down on alcohol, indicating he is not in this stage.
*Precontemplation*
- In this stage, individuals are **unaware or unwilling to acknowledge** that a problem exists.
- The patient clearly recognizes the problem and its consequences, ruling out precontemplation.
*Preparation*
- This stage involves **planning for change** and making small, tentative steps towards the desired behavior.
- While he expresses a desire to change, he hasn't articulated a concrete plan or taken any preparatory actions.
*Maintenance*
- This stage focuses on **sustaining the new behavior** and preventing relapse.
- The patient has not yet initiated the change, so he cannot be in the maintenance stage.
More P-values and confidence intervals US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.