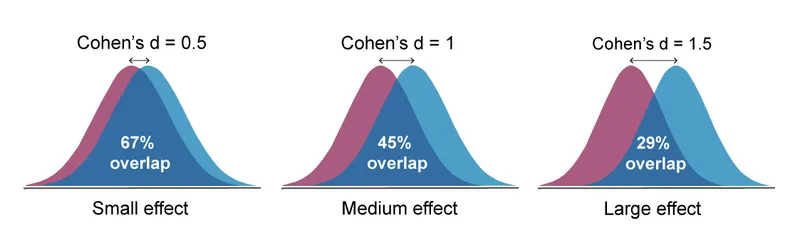
Effect size and clinical significance US Medical PG Practice Questions and MCQs
Practice US Medical PG questions for Effect size and clinical significance. These multiple choice questions (MCQs) cover important concepts and help you prepare for your exams.
Effect size and clinical significance US Medical PG Question 1: A randomized double-blind controlled trial is conducted on the efficacy of 2 different ACE-inhibitors. The null hypothesis is that both drugs will be equivalent in their blood-pressure-lowering abilities. The study concluded, however, that Medication 1 was more efficacious in lowering blood pressure than medication 2 as determined by a p-value < 0.01 (with significance defined as p ≤ 0.05). Which of the following statements is correct?
- A. We can accept the null hypothesis.
- B. We can reject the null hypothesis. (Correct Answer)
- C. This trial did not reach statistical significance.
- D. There is a 0.1% chance that medication 2 is superior.
- E. There is a 10% chance that medication 1 is superior.
Effect size and clinical significance Explanation: ***We can reject the null hypothesis.***
- A **p-value < 0.01** indicates that the observed difference is **statistically significant** at the **α = 0.05 level**, meaning there is strong evidence against the null hypothesis.
- When a result is statistically significant (p < α), we **reject the null hypothesis**. This is the standard statistical terminology for concluding that the observed effect is unlikely to be due to chance alone.
*We can accept the null hypothesis.*
- A **p-value < 0.01** is **less than the significance level of 0.05**, providing strong evidence to **reject the null hypothesis**, not accept it.
- Accepting the null hypothesis would imply there's no treatment effect, which contradicts the study's finding that Medication 1 was more efficacious.
- Note: In hypothesis testing, we never truly "accept" the null hypothesis; we either reject it or fail to reject it.
*This trial did not reach statistical significance.*
- The trial **did reach statistical significance** because the **p-value (p < 0.01) is less than the defined significance level (p ≤ 0.05)**.
- A p-value of 0.01 indicates a 1% chance that the observed results occurred by random chance if the null hypothesis were true.
*There is a 0.1% chance that medication 2 is superior.*
- The p-value of **p < 0.01** relates to the probability of observing the data (or more extreme data) given the null hypothesis is true, not the probability of one medication being superior.
- It does not directly provide the probability of Medication 2 being superior; rather, it indicates the **unlikelihood of the observed difference** if no true difference exists.
*There is a 10% chance that medication 1 is superior.*
- A **p-value of < 0.01** means there is **less than a 1% chance** of observing such a result if the null hypothesis (no difference) were true, not a 10% chance of superiority.
- The p-value represents the probability of observing the data, or more extreme data, assuming the **null hypothesis is true**, not the probability that one treatment is superior.
Effect size and clinical significance US Medical PG Question 2: A study is performed to determine the prevalence of a particular rare fungal pneumonia. A sample population of 100 subjects is monitored for 4 months. Every month, the entire population is screened and the number of new cases is recorded for the group. The data from the study are given in the table below:
Time point New cases of fungal pneumonia
t = 0 months 10
t = 1 months 4
t = 2 months 2
t = 3 months 5
t = 4 months 4
Which of the following is correct regarding the prevalence of this rare fungal pneumonia in this sample population?
- A. The prevalence at time point 2 months is 2%.
- B. The prevalence at time point 3 months is 11%.
- C. The prevalence at the conclusion of the study is 15%.
- D. The prevalence and the incidence at time point 2 months are equal.
- E. The prevalence at the conclusion of the study is 25%. (Correct Answer)
Effect size and clinical significance Explanation: ***The prevalence at the conclusion of the study is 25%***
- Prevalence is calculated by dividing the **total number of existing cases** by the total population at a specific point in time. At the conclusion of the study (t=4 months), the cumulative number of new cases is 10 + 4 + 2 + 5 + 4 = 25.
- The prevalence is therefore 25 cases / 100 subjects = **25%**.
*The prevalence at time point 2 months is 2%*
- At time point 2 months, the **cumulative number of new cases** is 10 (at t=0) + 4 (at t=1) + 2 (at t=2) = 16 cases.
- The prevalence at 2 months would be 16 cases / 100 subjects = **16%**, not 2%.
*The prevalence at time point 3 months is 11%*
- The cumulative number of new cases at time point 3 months is 10 (at t=0) + 4 (at t=1) + 2 (at t=2) + 5 (at t=3) = 21 cases.
- The prevalence at 3 months would be 21 cases / 100 subjects = **21%**, not 11%.
*The prevalence at the conclusion of the study is 15%*
- The cumulative number of new cases at the conclusion of the study (t=4 months) is 10 + 4 + 2 + 5 + 4 = **25 cases**.
- Therefore, the prevalence is 25 cases / 100 subjects = **25%**, not 15%.
*The prevalence and the incidence at time point 2 months are equal*
- **Incidence** refers to the number of *new* cases within a specified period, which at t=2 months is 2 cases.
- **Prevalence** at t=2 months is the cumulative number of cases (10+4+2 = 16 cases), so incidence (2%) and prevalence (16%) are **not equal**.
Effect size and clinical significance US Medical PG Question 3: Group of 100 medical students took an end of the year exam. The mean score on the exam was 70%, with a standard deviation of 25%. The professor states that a student's score must be within the 95% confidence interval of the mean to pass the exam. Which of the following is the minimum score a student can have to pass the exam?
- A. 45%
- B. 63.75%
- C. 67.5%
- D. 20%
- E. 65% (Correct Answer)
Effect size and clinical significance Explanation: ***65%***
- To find the **95% confidence interval (CI) of the mean**, we use the formula: Mean ± (Z-score × Standard Error). For a 95% CI, the Z-score is approximately **1.96**.
- The **Standard Error (SE)** is calculated as SD/√n, where n is the sample size (100 students). So, SE = 25%/√100 = 25%/10 = **2.5%**.
- The 95% CI is 70% ± (1.96 × 2.5%) = 70% ± 4.9%. The lower bound is 70% - 4.9% = **65.1%**, which rounds to **65%** as the minimum passing score.
*45%*
- This value is significantly lower than the calculated lower bound of the 95% confidence interval (approximately 65.1%).
- It would represent a score far outside the defined passing range.
*63.75%*
- This value falls below the calculated lower bound of the 95% confidence interval (approximately 65.1%).
- While close, this score would not meet the professor's criterion for passing.
*67.5%*
- This value is within the 95% confidence interval (65.1% to 74.9%) but is **not the minimum score**.
- Lower scores within the interval would still qualify as passing.
*20%*
- This score is extremely low and falls significantly outside the 95% confidence interval for a mean of 70%.
- It would indicate performance far below the defined passing threshold.
Effect size and clinical significance US Medical PG Question 4: You are conducting a study comparing the efficacy of two different statin medications. Two groups are placed on different statin medications, statin A and statin B. Baseline LDL levels are drawn for each group and are subsequently measured every 3 months for 1 year. Average baseline LDL levels for each group were identical. The group receiving statin A exhibited an 11 mg/dL greater reduction in LDL in comparison to the statin B group. Your statistical analysis reports a p-value of 0.052. Which of the following best describes the meaning of this p-value?
- A. There is a 95% chance that the difference in reduction of LDL observed reflects a real difference between the two groups
- B. Though A is more effective than B, there is a 5% chance the difference in reduction of LDL between the two groups is due to chance
- C. If 100 permutations of this experiment were conducted, 5 of them would show similar results to those described above
- D. This is a statistically significant result
- E. There is a 5.2% chance of observing a difference in reduction of LDL of 11 mg/dL or greater even if the two medications have identical effects (Correct Answer)
Effect size and clinical significance Explanation: **There is a 5.2% chance of observing a difference in reduction of LDL of 11 mg/dL or greater even if the two medications have identical effects**
- The **p-value** represents the probability of observing results as extreme as, or more extreme than, the observed data, assuming the **null hypothesis** is true (i.e., there is no true difference between the groups).
- A p-value of 0.052 means there's approximately a **5.2% chance** that the observed 11 mg/dL difference (or a more substantial difference) occurred due to **random variation**, even if both statins were equally effective.
*There is a 95% chance that the difference in reduction of LDL observed reflects a real difference between the two groups*
- This statement is an incorrect interpretation of the p-value; it confuses the p-value with the **probability that the alternative hypothesis is true**.
- A p-value does not directly tell us the probability that the observed difference is "real" or due to the intervention being studied.
*Though A is more effective than B, there is a 5% chance the difference in reduction of LDL between the two groups is due to chance*
- This statement implies that Statin A is more effective, which cannot be concluded with a p-value of 0.052 if the significance level (alpha) was set at 0.05.
- While it's true there's a chance the difference is due to chance, claiming A is "more effective" based on this p-value before statistical significance is usually declared is misleading.
*If 100 permutations of this experiment were conducted, 5 of them would show similar results to those described above*
- This is an incorrect interpretation. The p-value does not predict the outcome of repeated experiments in this manner.
- It refers to the **probability under the null hypothesis in a single experiment**, not the frequency of results across multiple hypothetical repetitions.
*This is a statistically significant result*
- A p-value of 0.052 is generally considered **not statistically significant** if the conventional alpha level (significance level) is set at 0.05 (or 5%).
- For a result to be statistically significant at alpha = 0.05, the p-value must be **less than 0.05**.
Effect size and clinical significance US Medical PG Question 5: A researcher is conducting a study to compare fracture risk in male patients above the age of 65 who received annual DEXA screening to peers who did not receive screening. He conducts a randomized controlled trial in 900 patients, with half of participants assigned to each experimental group. The researcher ultimately finds similar rates of fractures in the two groups. He then notices that he had forgotten to include 400 patients in his analysis. Including the additional participants in his analysis would most likely affect the study's results in which of the following ways?
- A. Wider confidence intervals of results
- B. Increased probability of committing a type II error
- C. Decreased significance level of results
- D. Increased external validity of results
- E. Increased probability of rejecting the null hypothesis when it is truly false (Correct Answer)
Effect size and clinical significance Explanation: ***Increased probability of rejecting the null hypothesis when it is truly false***
- Including more participants increases the **statistical power** of the study, making it more likely to detect a true effect if one exists.
- A higher sample size provides a more precise estimate of the population parameters, leading to a greater ability to **reject a false null hypothesis**.
*Wider confidence intervals of results*
- A larger sample size generally leads to **narrower confidence intervals**, as it reduces the standard error of the estimate.
- Narrower confidence intervals indicate **greater precision** in the estimation of the true population parameter.
*Increased probability of committing a type II error*
- A **Type II error** (false negative) occurs when a study fails to reject a false null hypothesis.
- Increasing the sample size typically **reduces the probability of a Type II error** because it increases statistical power.
*Decreased significance level of results*
- The **significance level (alpha)** is a pre-determined threshold set by the researcher before the study begins, typically 0.05.
- It is independent of sample size and represents the **acceptable probability of committing a Type I error** (false positive).
*Increased external validity of results*
- **External validity** refers to the generalizability of findings to other populations, settings, or times.
- While a larger sample size can enhance the representativeness of the study population, external validity is primarily determined by the **sampling method** and the study's design context, not just sample size alone.
Effect size and clinical significance US Medical PG Question 6: A study is being conducted on depression using the Patient Health questionnaire (PHQ-9) survey data embedded within a popular social media network with a response size of 500,000 participants. The sample population of this study is approximately normal. The mean PHQ-9 score is 14, and the standard deviation is 4. How many participants have scores greater than 22?
- A. 175,000
- B. 17,500
- C. 160,000
- D. 12,500 (Correct Answer)
- E. 25,000
Effect size and clinical significance Explanation: ***12,500***
- To find the number of participants with scores greater than 22, first calculate the **z-score** for a score of 22: $Z = \frac{(X - \mu)}{\sigma} = \frac{(22 - 14)}{4} = 2$.
- A z-score of 2 means the score is **2 standard deviations above the mean**. Using the **empirical rule** for a normal distribution, approximately **2.5%** of the data falls beyond 2 standard deviations above the mean (5% total in both tails, so 2.5% in each tail).
- Therefore, $2.5\%$ of the total 500,000 participants is $0.025 \times 500,000 = 12,500$.
*175,000*
- This option would imply a much larger proportion of the population scoring above 22, inconsistent with the **normal distribution's properties** and the calculated z-score.
- It would correspond to a z-score closer to 0, indicating a score closer to the mean, not two standard deviations above it.
*17,500*
- This value represents **3.5%** of the total population ($17,500 / 500,000 = 0.035$).
- A proportion of 3.5% above the mean corresponds to a z-score that is not exactly 2, indicating an incorrect calculation or interpretation of the **normal distribution table**.
*160,000*
- This option represents a very large portion of the participants, roughly **32%** of the total population.
- This percentage would correspond to scores within one standard deviation of the mean, not scores 2 standard deviations above the mean as calculated.
*25,000*
- This value represents **5%** of the total population ($25,000 / 500,000 = 0.05$).
- A z-score greater than 2 corresponds to the far tail of the normal distribution, where only 2.5% of the data lies, not 5%. This would correspond to a z-score of approximately 1.65.
Effect size and clinical significance US Medical PG Question 7: In a randomized controlled trial studying a new treatment, the primary endpoint (mortality) occurred in 14.4% of the treatment group and 16.7% of the control group. Which of the following represents the number of patients needed to treat to save one life, based on the primary endpoint?
- A. 1/(0.144 - 0.167)
- B. 1/(0.167 - 0.144) (Correct Answer)
- C. 1/(0.300 - 0.267)
- D. 1/(0.267 - 0.300)
- E. 1/(0.136 - 0.118)
Effect size and clinical significance Explanation: ***1/(0.167 - 0.144)***
- The **Number Needed to Treat (NNT)** is calculated as **1 / Absolute Risk Reduction (ARR)**.
- The **Absolute Risk Reduction (ARR)** is the difference between the event rate in the control group (16.7%) and the event rate in the treatment group (14.4%), which is **0.167 - 0.144**.
*1/(0.144 - 0.167)*
- This calculation represents 1 divided by the **Absolute Risk Increase**, which would be relevant if the treatment increased mortality.
- The **NNT should always be a positive value**, indicating the number of patients to treat to prevent one adverse event.
*1/(0.300 - 0.267)*
- This option uses arbitrary numbers (0.300 and 0.267) that do not correspond to the given **mortality rates** in the problem.
- It does not reflect the correct calculation for **absolute risk reduction** based on the provided data.
*1/(0.267 - 0.300)*
- This option also uses arbitrary numbers not derived from the problem's data, and it would result in a **negative value** for the denominator.
- The difference between event rates of 0.267 and 0.300 is not present in the given information for this study.
*1/(0.136 - 0.118)*
- This calculation uses arbitrary numbers (0.136 and 0.118) that are not consistent with the reported **mortality rates** of 14.4% and 16.7%.
- These values do not represent the **Absolute Risk Reduction** required for calculating NNT in this specific scenario.
Effect size and clinical significance US Medical PG Question 8: In 2013 the national mean score on the USMLE Step 1 exam was 227 with a standard deviation of 22. Assuming that the scores for 15,000 people follow a normal distribution, approximately how many students scored above the mean but below 250?
- A. 5,100 (Correct Answer)
- B. 4,500
- C. 6,000
- D. 3,750
- E. 6,750
Effect size and clinical significance Explanation: ***5,100***
- To solve this, first calculate the **z-score** for 250: (250 - 227) / 22 = 1.045.
- Using a **z-table**, the area under the curve from the mean (z=0) to z=1.045 is approximately 0.353. Multiplying this by 15,000 students gives approximately **5,295 students**, which is closest to 5,100.
*4,500*
- This answer would imply a smaller proportion of students between the mean and 250 (around 30%), which is lower than the calculated z-score of 1.045 suggests.
- It does not accurately reflect the area under the **normal distribution curve** for the given range.
*6,000*
- This option would mean that approximately 40% of students scored in this range, which would correspond to a z-score much higher than 1.045 or a different standard deviation.
- This calculation overestimates the number of students within the specified range.
*3,750*
- This value represents 25% of the total students (15,000 * 0.25), indicating that only a quarter of the distribution lies in this range.
- This significantly underestimates the proportion of students scoring between the mean and 250 for the given standard deviation.
*6,750*
- This option reflects approximately 45% of the total student population (15,000 * 0.45), which would correspond to a much larger z-score or a different distribution.
- This value is an overestimation and does not align with the standard normal distribution probabilities for the given parameters.
Effect size and clinical significance US Medical PG Question 9: An office team is being observed by an outside agency at the request of management to make sure they are completing all their tasks appropriately. Several of the employees are nervous that they are being watched and take care to perform their jobs with extra care, more so than they would have done during a normal workday. What best describes this behavior?
- A. Pygmalion effect
- B. Novelty effect
- C. Hawthorne effect (Correct Answer)
- D. Observer bias
- E. Ringelmann effect
Effect size and clinical significance Explanation: ***Hawthorne effect***
- The **Hawthorne effect** describes changes in behavior that occur among individuals who are aware that they are being observed.
- In this scenario, the employees' increased diligence due to being watched by an outside agency aligns perfectly with this psychological phenomenon.
*Pygmalion effect*
- The **Pygmalion effect** refers to the phenomenon where higher expectations lead to improved performance in a given area.
- It focuses on how an observer's expectations can influence the subject's behavior, rather than the subject's awareness of observation itself.
*Novelty effect*
- The **novelty effect** occurs when the initial interest or enthusiasm for a new item or intervention temporarily improves performance, which then wanes over time.
- This effect is related to the newness of a situation, not the act of being observed.
*Observer bias*
- **Observer bias** (also known as ascertainment bias) happens when the observer's expectations, beliefs, or preconceptions influence how they perceive or record data.
- It refers to a bias in the *observer*, not a change in the *observed subject's behavior* due to being watched.
*Ringelmann effect*
- The **Ringelmann effect** (or social loafing) describes the tendency for individual members of a group to become less productive as the size of their group increases.
- This is a phenomenon of reduced individual effort in a group setting, not an alteration in behavior due to being observed.
Effect size and clinical significance US Medical PG Question 10: A 45-year-old man presents for his annual checkup. The patient has a past medical history of diabetes mellitus (DM) type 2 that is well-controlled with diet. In addition, he was admitted to this hospital 1-year ago for a myocardial infarction (MI). The patient reports a 40-pack-year smoking history. However, after his MI, his doctors informed him about how detrimental smoking was to his heart condition. Since then, he has made efforts to cut down and now, for the past seven months, has stopped smoking. He says he used to use smoking as a means of dealing with his work and family stresses. He now attends wellness sessions at work and meditates early every morning before the family wakes up. Which of the following stages of the transtheoretical model is this patient most likely in?
- A. Preparation
- B. Contemplation
- C. Action
- D. Precontemplation
- E. Maintenance (Correct Answer)
Effect size and clinical significance Explanation: ***Maintenance***
- The patient has **successfully stopped smoking for seven months**, indicating sustained behavior change.
- He has also adopted **new coping mechanisms** like wellness sessions and meditation, which are crucial for preventing relapse and falls under this stage.
*Preparation*
- This stage involves **intending to take action** in the immediate future (e.g., within the next month) and involves some steps towards change, such as making a plan.
- The patient has already acted and sustained the behavior change, moving past mere preparation.
*Contemplation*
- Individuals in this stage are **aware a problem exists** and are seriously thinking about overcoming it but have not yet committed to taking action.
- The patient has clearly moved past just thinking about quitting and has actively stopped smoking.
*Action*
- This stage involves **modifying behavior, experiences, or environment** in order to overcome problems.
- While the patient was in the action stage when he initially quit, he has now maintained this change for an extended period (seven months), progressing beyond the initial action phase.
*Precontemplation*
- In this stage, individuals are **not intending to take action** in the foreseeable future (e.g., within 6 months) and are often unaware or underaware of their problems.
- This patient actively quit smoking and maintained cessation, showing he was not in precontemplation.
More Effect size and clinical significance US Medical PG questions available in the OnCourse app. Practice MCQs, flashcards, and get detailed explanations.