An investigator for a nationally representative health survey is evaluating the heights and weights of men and women aged 18–74 years in the United States. The investigator finds that for each sex, the distribution of heights is well-fitted by a normal distribution. The distribution of weight is not normally distributed. Results are shown: Mean Standard deviation Height (inches), men 69 0.1 Height (inches), women 64 0.1 Weight (pounds), men 182 1.0 Weight (pounds), women 154 1.0 Based on these results, which of the following statements is most likely to be correct?

99.7% of heights in women are likely to fall between 63.7 and 64.3 inches.

86% of heights in women are likely to fall between 63.9 and 64.1 inches.

68% of weights in women are likely to fall between 153 and 155 pounds.

95% of heights in men are likely to fall between 68.85 and 69.15 inches.

99.7% of heights in men are likely to fall between 68.8 and 69.2 inches.

A neuro-oncology investigator has recently conducted a randomized controlled trial in which the addition of a novel alkylating agent to radiotherapy was found to prolong survival in comparison to radiotherapy alone (HR = 0.7, p < 0.01). A number of surviving participants who took the alkylating agent reported that they had experienced significant nausea from the medication. The investigator surveyed all participants in both the treatment and the control group on their nausea symptoms by self-report rated mild, moderate, or severe. The investigator subsequently compared the two treatment groups with regards to nausea level. | | Mild nausea | Moderate nausea | Severe nausea | |---|---|---|---| | Treatment group (%) | 20 | 30 | 50 | | Control group (%) | 35 | 35 | 30 | Which of the following statistical methods would be most appropriate to assess the statistical significance of these results?

Pearson correlation coefficient

A student health coordinator plans on leading a campus-wide HIV screening program that will be free for the entire undergraduate student body. The goal is to capture as many correct HIV diagnoses as possible with the fewest false positives. The coordinator consults with the hospital to see which tests are available to use for this program. Test A has a sensitivity of 0.92 and a specificity of 0.99. Test B has a sensitivity of 0.95 and a specificity of 0.96. Test C has a sensitivity of 0.98 and a specificity of 0.93. Which of the following testing schemes should the coordinator pursue?

Test C on the entire student body followed by Test A on those who are positive

Test A on the entire student body followed by Test B on those who are positive

Test A on the entire student body followed by Test C on those who are positive

Test C on the entire student body followed by Test B on those who are positive

Test B on the entire student body followed by Test A on those who are positive

Ethics/Biostatistics | Behavioral Science

📊 Statistical Foundation Mastery: The Numbers That Drive Medicine

Medical decisions rest on two pillars: doing what's right and knowing what's true. This lesson equips you to navigate both-mastering the ethical frameworks that guide patient care and the statistical tools that transform raw data into reliable evidence. You'll learn to recognize distribution patterns in clinical datasets, select appropriate tests for different research questions, quantify uncertainty with precision, and integrate these skills into the critical thinking physicians use daily. By connecting moral reasoning with mathematical rigor, you'll build the foundation for evidence-based practice that honors both science and humanity.

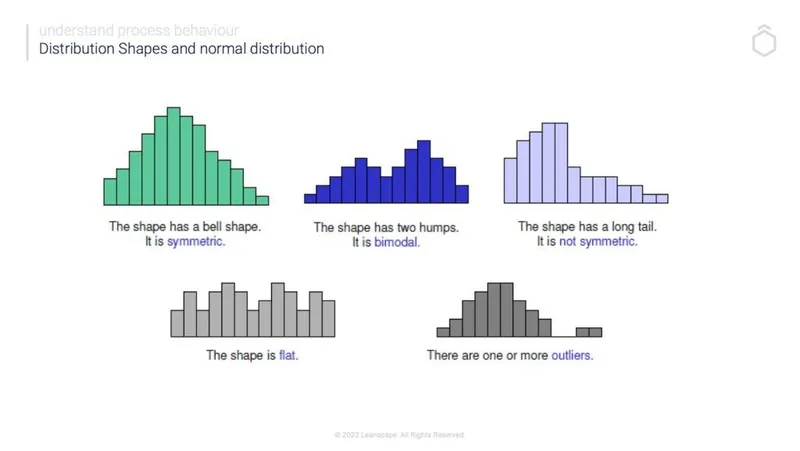
Statistical distribution curves showing normal, skewed, and bimodal patterns in medical data

Central Tendency: The Heart of Your Data

Central tendency measures reveal the "typical" value in medical datasets, but each measure tells a different clinical story:

Mean (Arithmetic Average)
- Most sensitive to extreme values (outliers)
- Best for: normally distributed continuous data
- Clinical use: laboratory reference ranges, drug dosing calculations
- Formula: $\bar{x} = \frac{\sum x_i}{n}$
Median (Middle Value)
- Resistant to outliers and skewed distributions
- Best for: non-normal data, ordinal scales
- Clinical use: hospital length of stay, pain scores
- Position: 50th percentile of ordered data
Mode (Most Frequent Value)
- Only measure applicable to categorical data
- Best for: nominal variables, discrete counts
- Clinical use: most common diagnosis, preferred treatment choice

📌 Remember: MOM - Mean for normal distributions, Outlier-resistant median for skewed data, Mode for categories. Mean pulls toward outliers, median stays centered, mode shows peaks.

Dispersion Measures: Quantifying Clinical Variability

Dispersion measures reveal how spread out your data points are, critical for understanding treatment consistency and population heterogeneity:

Measure	Formula	Outlier Sensitivity	Best Use	Clinical Example
Range	Max - Min	Extremely high	Quick assessment	Blood pressure readings
Interquartile Range	Q3 - Q1	Low	Skewed data	Hospital costs
Variance	$s^2 = \frac{\sum(x_i - \bar{x})^2}{n-1}$	High	Theoretical work	Research calculations
Standard Deviation	$s = \sqrt{s^2}$	High	Normal distributions	Lab reference ranges
Coefficient of Variation	$CV = \frac{s}{\bar{x}} \times 100%$	Moderate	Comparing variability	Drug concentration studies

Understanding dispersion patterns reveals critical clinical insights about treatment reliability and patient population characteristics.

📊 Statistical Foundation Mastery: The Numbers That Drive Medicine

Descriptive statistics (central tendency, dispersion)

Inferential statistics

🎯 Distribution Architecture: The Shape of Medical Reality

Normal Distribution: The Statistical Gold Standard

The normal distribution (Gaussian curve) represents the foundation of parametric statistics, characterized by:

Perfect symmetry around the mean
Bell-shaped curve with single peak
Mean = Median = Mode (all central measures identical)
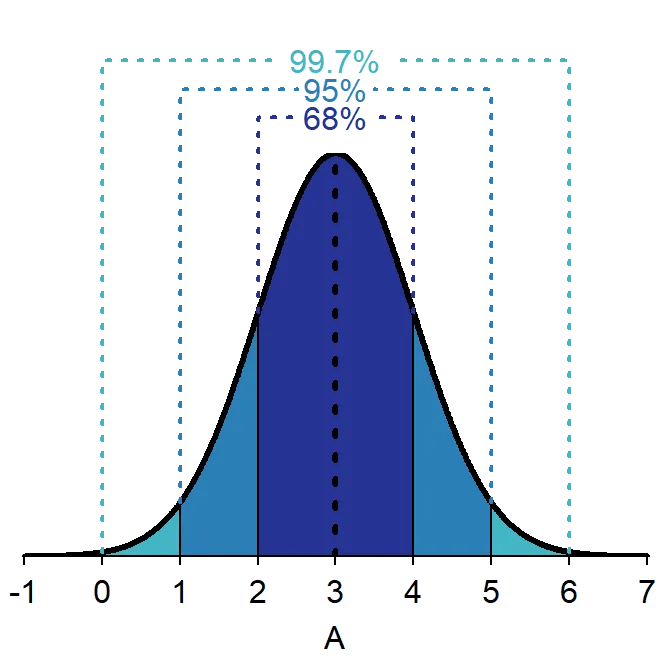
68-95-99.7 rule for standard deviation intervals
Asymptotic tails approaching but never touching zero

💡 Master This: Normal distributions enable powerful parametric tests (t-tests, ANOVA, regression) that provide maximum statistical power. When data follows normal patterns, you can make precise probability statements about individual values and population parameters.

Clinical Examples of Normal Distributions:

Adult height and weight measurements
Blood pressure in healthy populations
Many laboratory values (hemoglobin, cholesterol)
IQ scores and cognitive assessments
Drug plasma concentrations at steady state

Skewed Distributions: When Reality Bends the Curve

Skewed distributions occur frequently in medical data, requiring different analytical approaches:

Right-Skewed (Positive Skew):

Tail extends toward higher values
Mean > Median > Mode
Common in medical data due to biological constraints
Examples: hospital length of stay, healthcare costs, reaction times
Analysis: Use median and IQR; consider log transformation

Left-Skewed (Negative Skew):

Tail extends toward lower values
Mode > Median > Mean
Less common in medical settings
Examples: age at death in developed countries, test scores with ceiling effects
Analysis: Use median and IQR; consider reflection then log transformation

📌 Remember: TAIL tells the TALE - Skewness direction follows the tail. Right skew = positive skew = tail points right. Left skew = negative skew = tail points left. The mean always chases the tail.

Bimodal and Multimodal Patterns

Multiple peaks in distributions often reveal clinically significant subpopulations:

Bimodal: Two distinct peaks suggesting two populations
Multimodal: Multiple peaks indicating several subgroups
Clinical significance: May indicate different disease phenotypes, treatment responders vs. non-responders, or demographic subgroups

Recognition Strategy:

Look for multiple peaks in histograms
Check for plateau regions between peaks
Consider mixture models for analysis
Investigate clinical subgroups that might explain patterns

⭐ Clinical Pearl: Bimodal distributions in treatment response data often indicate responder vs. non-responder populations. This pattern suggests the need for personalized medicine approaches or biomarker-guided therapy selection.

Distribution recognition connects directly to appropriate statistical test selection and clinical interpretation frameworks.

🎯 Distribution Architecture: The Shape of Medical Reality

Descriptive statistics (central tendency, dispersion)

📐 Variability Quantification: Measuring Clinical Precision

Standard Deviation: The Clinical Workhorse

Standard deviation quantifies average distance from the mean, providing the foundation for most clinical reference ranges and statistical tests:

Calculation Process:

Calculate mean: $\bar{x} = \frac{\sum x_i}{n}$
Find deviations: $(x_i - \bar{x})$ for each value
Square deviations: $(x_i - \bar{x})^2$
Sum squared deviations: $\sum(x_i - \bar{x})^2$
Divide by (n-1): $s^2 = \frac{\sum(x_i - \bar{x})^2}{n-1}$
Take square root: $s = \sqrt{s^2}$

💡 Master This: Standard deviation shares the same units as your original data, making it clinically interpretable. A hemoglobin SD of 1.2 g/dL means typical values vary by ±1.2 g/dL from the average, directly applicable to clinical decision-making.

Clinical Applications:

Laboratory reference ranges: Mean ± 2 SD captures 95% of healthy population
Quality control: Values beyond 3 SD trigger investigation
Treatment monitoring: Changes >2 SD suggest real clinical change
Research power: Smaller SD increases ability to detect treatment effects

Diagram showing standard deviation intervals and percentage of data captured in normal distribution

Coefficient of Variation: Standardized Comparison Tool

The coefficient of variation (CV) enables comparison of variability across different scales and units:

$$CV = \frac{\text{Standard Deviation}}{\text{Mean}} \times 100%$$

Interpretation Guidelines:

CV < 10%: Low variability, high precision
CV 10-20%: Moderate variability, acceptable precision
CV 20-30%: High variability, concerning precision
CV > 30%: Very high variability, poor precision

Laboratory Test	Typical CV	Clinical Interpretation
Glucose	3-5%	Excellent precision
Cholesterol	2-4%	Excellent precision
Creatinine	4-8%	Good precision
Troponin	8-15%	Acceptable precision
PSA	15-25%	Moderate precision

Robust Measures: Outlier-Resistant Alternatives

When data contains outliers or follows non-normal distributions, robust measures provide more reliable variability assessment:

Interquartile Range (IQR):

Definition: Q3 - Q1 (75th percentile - 25th percentile)
Advantage: Unaffected by extreme values
Clinical use: Skewed data like hospital costs, length of stay
Outlier detection: Values beyond Q1 - 1.5×IQR or Q3 + 1.5×IQR

Median Absolute Deviation (MAD):

Definition: Median of absolute deviations from median
Advantage: Extremely robust to outliers
Clinical use: When extreme outliers present
Calculation: MAD = median(|xi - median(x)|)

⭐ Clinical Pearl: IQR captures the middle 50% of your data, providing outlier-resistant spread measurement. In skewed medical data (costs, length of stay), IQR often provides more clinically meaningful variability assessment than standard deviation.

Robust measures ensure accurate variability assessment even when data violates normal distribution assumptions.

📐 Variability Quantification: Measuring Clinical Precision

Effect size and clinical significance

P-values and confidence intervals

🔍 Pattern Recognition Mastery: Identifying Distribution Signatures

Visual Pattern Recognition Framework

Step 1: Overall Shape Assessment

Symmetrical: Consider normal distribution
Single tail extension: Identify skew direction
Multiple peaks: Look for bimodal/multimodal patterns
Flat appearance: Suspect uniform distribution
Extreme outliers: Consider contaminated normal

Step 2: Central Tendency Relationships

Mean ≈ Median ≈ Mode: Strong normal distribution evidence
Mean > Median: Right skew pattern
Mean < Median: Left skew pattern
Multiple modes: Multimodal distribution confirmed

Step 3: Tail Behavior Analysis

Symmetric tails: Normal or other symmetric distributions
Heavy tails: Consider t-distribution or contaminated normal
Light tails: Possible uniform or truncated distribution
Asymmetric tails: Confirms skewness direction

💡 Master This: The Mean-Median relationship provides the fastest distribution assessment. In right-skewed data, extreme high values pull the mean above the median. In left-skewed data, extreme low values pull the mean below the median.

Statistical Tests for Normality

Shapiro-Wilk Test:

Best for: Small samples (n < 50)
Null hypothesis: Data follows normal distribution
Interpretation: p < 0.05 suggests non-normality
Advantage: Most powerful normality test for small samples

Kolmogorov-Smirnov Test:

Best for: Large samples (n > 50)
Null hypothesis: Data follows specified distribution
Interpretation: p < 0.05 suggests distribution mismatch
Advantage: Can test against any specified distribution

Anderson-Darling Test:

Best for: Moderate samples (n = 20-100)
Null hypothesis: Data follows normal distribution
Interpretation: p < 0.05 suggests non-normality
Advantage: More sensitive to tail deviations

Sample Size	Recommended Test	Critical p-value	Action if p < 0.05
n < 20	Visual inspection	N/A	Use non-parametric tests
n = 20-50	Shapiro-Wilk	0.05	Consider transformation
n = 50-100	Anderson-Darling	0.05	Use robust methods
n > 100	Kolmogorov-Smirnov	0.05	Apply CLT principles

Clinical Context Pattern Recognition

Biological Constraint Patterns:

Floor effects: Minimum possible values (reaction times, survival times)
Ceiling effects: Maximum possible values (test scores, age at death)
Natural boundaries: Physical limits creating skewness

Population Mixture Patterns:

Bimodal age distributions: Pediatric vs. adult populations
Treatment response patterns: Responders vs. non-responders
Disease severity patterns: Mild vs. severe phenotypes

Measurement Artifact Patterns:

Digit preference: Rounding to preferred numbers (0, 5)
Detection limits: Laboratory assay thresholds
Reporting bias: Selective outcome reporting

⭐ Clinical Pearl: Bimodal distributions in clinical data often indicate two distinct populations that should be analyzed separately. This pattern frequently reveals important clinical subgroups requiring different treatment approaches.

Pattern recognition skills directly translate to appropriate statistical test selection and meaningful clinical interpretation.

🔍 Pattern Recognition Mastery: Identifying Distribution Signatures

Hypothesis testing

Type I and Type II errors

⚖️ Statistical Test Selection: Matching Methods to Data Reality

Parametric Test Requirements

Fundamental Assumptions:

Normality: Data follows normal distribution
Independence: Observations unrelated to each other
Homoscedasticity: Equal variances across groups
Linearity: Relationships follow straight-line patterns (regression)

When Assumptions Met:

Maximum statistical power to detect differences
Precise confidence intervals and p-values
Robust to minor assumption violations with adequate sample size
Interpretable effect sizes with clinical meaning

Common Parametric Tests:

One-sample t-test: Compare sample mean to known value
Two-sample t-test: Compare means between two groups
Paired t-test: Compare before/after measurements
ANOVA: Compare means across multiple groups
Linear regression: Model continuous outcome relationships

💡 Master This: Parametric tests provide maximum power when assumptions are met, but can produce misleading results when assumptions are violated. The trade-off between power and robustness drives test selection decisions.

Non-Parametric Alternatives

Key Advantages:

Distribution-free: No normality assumptions required
Robust to outliers: Extreme values don't distort results
Applicable to ordinal data: Works with ranked measurements
Fewer assumptions: More broadly applicable

Power Trade-offs:

80-95% efficiency compared to parametric tests when normality holds
Superior performance when assumptions violated
Broader applicability across data types and distributions

Parametric Test	Non-Parametric Alternative	Use When
One-sample t-test	Wilcoxon signed-rank	Non-normal, small sample
Two-sample t-test	Mann-Whitney U	Skewed data, outliers
Paired t-test	Wilcoxon signed-rank	Non-normal differences
One-way ANOVA	Kruskal-Wallis	Non-normal, unequal variances
Pearson correlation	Spearman correlation	Non-linear relationships

Sample Size Considerations

Small Samples (n < 30):

Normality testing unreliable: Visual inspection preferred
Non-parametric tests safer: Less assumption-dependent
Exact tests available: Provide precise p-values
Bootstrap methods: Generate empirical distributions

Large Samples (n > 100):

Central Limit Theorem applies: Means approach normality
Parametric tests robust: Minor assumption violations acceptable
Asymptotic methods valid: Large-sample approximations accurate
Effect size emphasis: Statistical significance easier to achieve

Moderate Samples (n = 30-100):

Formal normality testing: Shapiro-Wilk, Anderson-Darling
Assumption checking critical: Moderate power for detection
Transformation options: Log, square root, Box-Cox
Robust methods: Trimmed means, bootstrap confidence intervals

⭐ Clinical Pearl: With n > 100, the Central Limit Theorem ensures that sample means follow normal distributions even when individual observations don't. This enables parametric test use even with moderately skewed data.

Statistical test selection directly impacts the validity and interpretability of research findings and clinical conclusions.

⚖️ Statistical Test Selection: Matching Methods to Data Reality